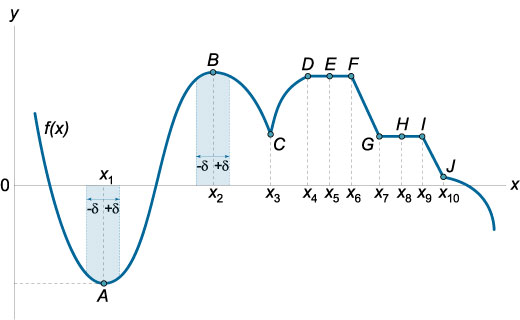
отсутствие инвариантности формы у дифференциалов высших порядков
Отсутствие инвариантности формы у дифференциалов высших порядков
Дифференциалы высших порядков.
Аналогично, дифференциалом n-го порядка называется дифференциал от дифференциала (n-1)-го порядка
Здесь через обозначен квадрат приращения независимого аргумента
Некоторая несимметричность обозначения числителя и знаменателя дроби отражается и в прочтении этого выражения:» д два игрек по икс квадрат (или по икс дважды)».
Неинвариантность старших дифференциалов.
Инвариантность формы первого дифференциала не удается обобщить на дифференциалы высших порядков.
Формула для вычисления второго дифференциала в первом случае получена выше.
Поэтому, находя дифференциал второго порядка, мы уже не можем просто вынести за знак производной, а вынуждены использовать формулу дифференциала произведения.
Как видно, формула второго дифференциала сложной функции отличается от формулы для случая независимого аргумента благодаря наличию второго слагаемого, содержащего второй дифференциал аргумента.
Для высших диффернциалов формулы еще сложнее, и, значит, свойство инвариантности формы присуще только первому дифференциалу.
22. Производные и дифференциалы высших порядков. Неинвариантность формы второго дифференциала.
Производные высших порядков.
Пусть функция y=f(x) дифференцируемая на некотором промежутке. Производная у’=f'(х) называется производной 1-го порядка и представляет собой так же функцию от х.
Производная от производной 1-го порядка – называется производной 2-го порядка от функции у=f(x) и обозначается у», илиf»(х), илиd²y/dx², (d/dx)*(dy/dx),dy’/dx. Таким образом, у»=(у’)’. Аналогично от производной 2-го порядка, если она существует, называется производной третьего порядка от функции у=f(x). Обобщив скажем, что производнаяn-го порядка от заданной функции у=f(х), если она существует, называется производной от производной (n-1)-го порядка.
Примечания: Что бы найти производную n-го порядка, надо найти все предшествующие производные до (n-1)-го порядка включительно.
Производные выше 1-го порядка называются производными высших порядков. Начиная с производной 4-го порядка, производные обозначаются римскими цифрами или числами в скобках.
Пусть у=U*V,U=U(x),V=V(x) – некоторые функции имеющие производные любого порядка. Формула Лейбница имеет вид:
Как видно, коэффициент в формуле Лейбница то же, что и в разложении Бинома-Ньютона
Дифференциалы высших порядков.
Пусть функция у=f(x) –дифференцируемая функция, а ее аргумент х – независимая переменная. Согласно определению дифференциала функции(dy=f'(х)*dx), есть так же функция от х, можно найти дифференциал от этой функции.
Определение: Дифференциал от дифференциала dyназывается дифференциалом второго порядка функции у=f(x) и обозначается(d²y). Таким образом, по определению имеемd²y=d(dy)=(dy’)*dx=(f ’(x)*dx)’*dx=f»(x)*(dx)².
Определение: Аналогично дифференциал от дифференциала второго порядка называется дифференциалом третьего порядка(d³y).
Обобщим, получим что дифференциал n-го порядка функции у=f(х) определяется, как дифференциал от дифференциала (n-1)-го порядка этой функции(обозначение). Отсюда можно найти
Замечание: Дифференциалы высших порядков (начиная со второго) свойством инвариантности не обладают, т.е. выражение для дифференциала различных порядков справедливы только в том случае, когда есть независимая переменная величина.
y”(x)=
d ( n ) (y)=y ( n ) (x)∙dx n
d 2 y=y”(t)∙dt 2 =[y”(x)(x’(t)) 2 +y’(x)∙x”(t)]dt 2 =y”(x)∙[x’(t)∙dt] 2 +y’(x)∙x”(t)∙dt 2
d 2 y=y”(x)∙dx 2 +y’(x)∙d 2 x
Форма 2-го диф-ла не инвариантна отн-но зависимости аргумента.
23. Производные функций, заданных параметрически.
Часто зависимость между переменными х и у задается параметрическими уравнениями:
y=g(t), гдеt– вспомогательная переменная называемая параметром.
Если функция (t) иg(t) дифференцировались и'(t)0, то производнаяdy/dxот функции у по аргументу х может быть найдена, как отношение дифференциаловdyиdx, т.к.dy=g'(t)*dt, иdy/dx=(g'(t)*dt)/('(t)*dt)=(dy/dt)/(dx/dt)=Yt’/Xt’, то естьdy/dx=Yt’/Xt’
22. Производные и дифференциалы высших порядков. Неинвариантность формы второго дифференциала.
Производные высших порядков.
Пусть функция y=f(x) дифференцируемая на некотором промежутке. Производная у’=f ‘(х) называется производной 1-го порядка и представляет собой так же функцию от х.
Производная от производной 1-го порядка – называется производной 2-го порядка от функции у=f(x) и обозначается у», или f »(х), или d ²y/dx², (d/dx)*(dy/dx), dy’/dx. Таким образом, у»=(у’)’. Аналогично от производной 2-го порядка, если она существует, называется производной третьего порядка от функции у=f(x). Обобщив скажем, что производная n-го порядка от заданной функции у=f(х), если она существует, называется производной от производной (n-1)-го порядка.
Примечания: Что бы найти производную n-го порядка, надо найти все предшествующие производные до (n-1)-го порядка включительно.
Производные выше 1-го порядка называются производными высших порядков. Начиная с производной 4-го порядка, производные обозначаются римскими цифрами или числами в скобках.
Пусть у=U*V, U=U(x), V=V(x) – некоторые функции имеющие производные любого порядка. Формула Лейбница имеет вид:
Как видно, коэффициент в формуле Лейбница то же, что и в разложении Бинома-Ньютона
Дифференциалы высших порядков.
Пусть функция у=f(x) –дифференцируемая функция, а ее аргумент х – независимая переменная. Согласно определению дифференциала функции(dy=f ‘(х)*dx), есть так же функция от х, можно найти дифференциал от этой функции.
Определение: Дифференциал от дифференциала dy называется дифференциалом второго порядка функции у=f(x) и обозначается(d²y). Таким образом, по определению имеем d²y=d(dy)=(dy’)*dx=(f ’(x)*dx)’*dx=f »(x)*(dx)².
Определение: Аналогично дифференциал от дифференциала второго порядка называется дифференциалом третьего порядка(d³y).
Обобщим, получим что дифференциал n-го порядка функции у=f(х) определяется, как дифференциал от дифференциала (n-1)-го порядка этой функции(обозначение). Отсюда можно найти 
Замечание: Дифференциалы высших порядков (начиная со второго) свойством инвариантности не обладают, т.е. выражение для дифференциала различных порядков справедливы только в том случае, когда есть независимая переменная величина.
y”(x)=
d ( n ) (y)=y ( n ) (x)∙dx n
d 2 y=y”(t)∙dt 2 =[y”(x)(x’(t)) 2 +y’(x)∙x”(t)]dt 2 =y”(x)∙[x’(t)∙dt] 2 +y’(x)∙x”(t)∙dt 2
d 2 y=y”(x)∙dx 2 +y’(x)∙d 2 x
Форма 2-го диф-ла не инвариантна отн-но зависимости аргумента.
23. Производные функций, заданных параметрически.
Часто зависимость между переменными х и у задается параметрическими уравнениями:
y=g(t), где t – вспомогательная переменная называемая параметром.
Если функция (t) и g(t) дифференцировались и '(t)0, то производная dy/dx от функции у по аргументу х может быть найдена, как отношение дифференциалов dy и dx, т.к. dy=g'(t)*dt, и dy/dx=(g'(t)*dt)/('(t)*dt)=(dy/dt)/(dx/dt)=Yt’/Xt’, то есть dy/dx=Yt’/Xt’
22. Производные и дифференциалы высших порядков. Неинвариантность формы второго дифференциала.
Производные высших порядков.
Пусть функция y=f(x) дифференцируемая на некотором промежутке. Производная у’=f'(х) называется производной 1-го порядка и представляет собой так же функцию от х.
Производная от производной 1-го порядка – называется производной 2-го порядка от функции у=f(x) и обозначается у», илиf»(х), илиd²y/dx², (d/dx)*(dy/dx),dy’/dx. Таким образом, у»=(у’)’. Аналогично от производной 2-го порядка, если она существует, называется производной третьего порядка от функции у=f(x). Обобщив скажем, что производнаяn-го порядка от заданной функции у=f(х), если она существует, называется производной от производной (n-1)-го порядка.
Примечания: Что бы найти производную n-го порядка, надо найти все предшествующие производные до (n-1)-го порядка включительно.
Производные выше 1-го порядка называются производными высших порядков. Начиная с производной 4-го порядка, производные обозначаются римскими цифрами или числами в скобках.
Пусть у=U*V,U=U(x),V=V(x) – некоторые функции имеющие производные любого порядка. Формула Лейбница имеет вид:
Как видно, коэффициент в формуле Лейбница то же, что и в разложении Бинома-Ньютона
Дифференциалы высших порядков.
Пусть функция у=f(x) –дифференцируемая функция, а ее аргумент х – независимая переменная. Согласно определению дифференциала функции(dy=f'(х)*dx), есть так же функция от х, можно найти дифференциал от этой функции.
Определение: Дифференциал от дифференциала dyназывается дифференциалом второго порядка функции у=f(x) и обозначается(d²y). Таким образом, по определению имеемd²y=d(dy)=(dy’)*dx=(f ’(x)*dx)’*dx=f»(x)*(dx)².
Определение: Аналогично дифференциал от дифференциала второго порядка называется дифференциалом третьего порядка(d³y).
Обобщим, получим что дифференциал n-го порядка функции у=f(х) определяется, как дифференциал от дифференциала (n-1)-го порядка этой функции(обозначение). Отсюда можно найти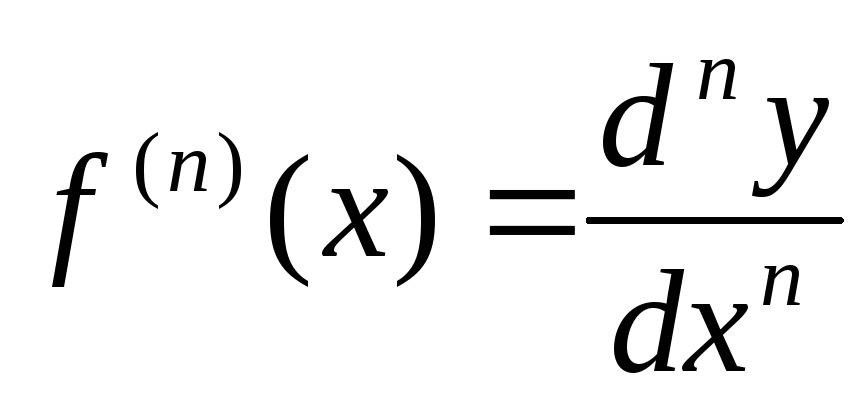
Замечание: Дифференциалы высших порядков (начиная со второго) свойством инвариантности не обладают, т.е. выражение для дифференциала различных порядков справедливы только в том случае, когда есть независимая переменная величина.
y”(x)=
d ( n ) (y)=y ( n ) (x)∙dx n
d 2 y=y”(t)∙dt 2 =[y”(x)(x’(t)) 2 +y’(x)∙x”(t)]dt 2 =y”(x)∙[x’(t)∙dt] 2 +y’(x)∙x”(t)∙dt 2
d 2 y=y”(x)∙dx 2 +y’(x)∙d 2 x
Форма 2-го диф-ла не инвариантна отн-но зависимости аргумента.
23. Производные функций, заданных параметрически.
Часто зависимость между переменными х и у задается параметрическими уравнениями:
y=g(t), гдеt– вспомогательная переменная называемая параметром.
Если функция (t) иg(t) дифференцировались и'(t)0, то производнаяdy/dxот функции у по аргументу х может быть найдена, как отношение дифференциаловdyиdx, т.к.dy=g'(t)*dt, иdy/dx=(g'(t)*dt)/('(t)*dt)=(dy/dt)/(dx/dt)=Yt’/Xt’, то естьdy/dx=Yt’/Xt’
Дифференциалы высших порядков



Производные и дифференциалы высших порядков.
Производные и дифференциалы высших порядков
Если первая производная функция y = f ‘(x) дифференцируема в интервале (a, b), то ее производная называется второй производной функции f(x).
Вторая производная обозначается символами f »(x) или
Вообще, производной n–го порядка функции f(x), называется производная от производной функции f(x) (n − 1)–го порядка. Производная n–го порядка обозначается f (n) (x).
Замечание. Если речь идет о производной n–го порядка ( n = 2, 3, … ) в фиксированной точке x0, то для существования f (n) (x0) необходимо существование f (n − 1) (x) не только в точке x0, но и в некоторой ее окрестности. При этом условии
Функция, имеющая в точке производную n–го порядка, называется n раз дифференцируемой в этой точке.
Функция, имеющая в точке производные всех порядков, называется бесконечно дифференцируемой в этой точке.
Формулы для производных n–го порядка суммы и произведения функций
Если функции u(x) и v(x) n раз дифференцируемы на некотором промежутке, то производная n–го порядка суммы определяется формулой
а производная n–го порядка произведения определяется формулой Лейбница
( u · v) (n) = u (n) · v + n u (n − 1) · v‘ +
Формула Лейбница может быть записана в виде
|





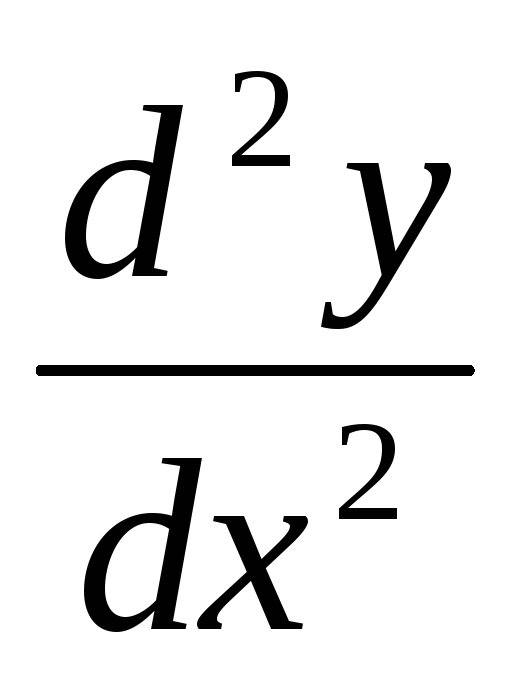









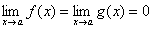 или
или 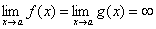 . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций 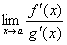 , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем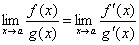
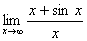 . Этот предел существует
. Этот предел существует 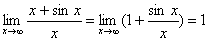 . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
. Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.