отношения между сложными суждениями логика
Отношения между сложными суждениями. Понятие логического следования.



Сравнимыминазываются сложные суждения, в состав которых входит хотя бы одна общая переменная, соответствующая простым суждениям.
Среди сравнимых суждений выделяют совместимые и несовместимые суждения.
Между совместимыми суждениями возникают отношения эквивалентности, логического следования, частичной совместимости.
Между несовместимыми суждениями возникают противоречие и противоположность
Эквивалентнымиявляются суждения, которые принимают одинаковые значения при одних и тех же значениях составляющих.
Эквивалентность позволяет нам выделить суждения с различными смыслами, но с одинаковыми значениями.
Суждения находятся в отношении логического следования, если не может быть так, чтобы первое суждение было истинным, а второе – ложным. Это самое важное отношение в логике, т.к. оно лежит в основе дедуктивных умозаключений. Обозначается так: « |= » (= «логически следует»)
Отношение частичной совместимости означает, что в построенной для них совместной семантической таблице суждения не могут одновременно принимать значение «ложь», но при этом могут встречаться другие комбинации.
Противоречие между сложными суждениями, как и между простыми, проявляется в том, что вместе они не могут быть ни истинными, ни ложными.
Суждения же, находящиеся в отношении противоположности, не могут быть вместе истинными, но могут быть вместе ложными.
Законы логики и логические противоречия.
Основные законы логики.
Выделяется четыре основных закона:
В схеме выражается формулой: А→А ( Если А, то А)
или: А=А (А тогда и только тогда, когда А).
Содержательная формулировка: «Один и тот же термин в одном и том же рассуждении должен употребляться в одном и том же отношении, в одном и том же смысле и применительно к одному и тому же времени».
2. Закон непротиворечия.
Формула такова: (А&A), т.е «Неверно, что А и не-А». Формула (А&A) называется противоречием. Закон указывает на его недопустимость.
Содержательная формулировка: «Невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении».
3. Закон исключенного третьего.
Содержательная формулировка: «Из двух противоречащих суждений истинным следует считать только одно».
4. Закон достаточного основания.
Содержательная формулировка: «Никакое высказывание А не может утверждаться без достаточного основания.
Шпаргалка по логике.
24. СЛОЖНЫЕ СУЖДЕНИЯ, ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ.
Сложные суждения образуются из простых путем их соединения. Сложные суждения могут быть истинными или ложными, истинность или ложность которых зависит прежде всего от истинности или ложности составляющих его простых и иных суждений.
В сложных суждениях, в отличие от простых, одновременно раскрывается не одна, а несколько связей между предметами мысли. Основными структурообразующими элементами выступают самостоятельные суждения.
Не всякое сложное суждение выражается сложным предложением, но всякое сложное предложение выражает сложное суждение.
Выделяют следующие виды сложных суждений: 1)соединительные (конъюнкция);
2) разделительные (дизъюнкция);
3) условные (импликация);
4) эквивалентные. Конъюнкция – образуется из нескольких простых,
Связанных логической связкой «и». Например, «Никто не забыт и ничто не забыто» – А В. (Где А – Никто не забыт; В – ничто не забыто. А и В – члены конъюнкции).
Для конъюнкции свойственна взаимозаменяемость положения членов конъюнкции: А В, или В А.
Дизъюнкция состоит из нескольких простых, связанных логической связкой «или»: А V В.
Выделяют две разновидности разделительного суждения:
1) нестрогую (слабую) дизъюнкцию;
2) строгую (сильную) дизъюнкцию.
Слабая дизъюнкция – объединяемые ею суждения не исключают друг друга, т. е. вместо «или» можно поставить «и» (символ V). Слабая дизъюнкция истинна в тех случаях, когда истинно одно из суждений (или оба), и ложна, когда оба суждения ложны.
Сильная дизъюнкция – образуется логической связкой «либо», и ее составляющие исключают друг друга. Строгая дизъюнкция истинна только тогда, когда одно из суждений истинно, а другое – ложно.
Импликация – суждения объединяются на основе логической связки «если. то», например: «Если будет хорошая погода, то соревнования состоятся».
Эквивалентные суждения – это суждения с взаимной условной зависимостью, выражаемые логической связкой «если и только если. то. ». Например, если и только если человек достиг пенсионного возраста, то он имеет право на получение пенсии по возрасту.
Между сложными суждениями существуют определенные отношения, они могут быть совместимыми и несовместимыми.
Совместимые суждения – это суждения, которые могут быть одновременно истинными.
Выделяют три вида совместимости сложных суждений:
2) частичная совместимость;
Эквивалентными являются суждения, являющиеся истинными или ложными одновременно.
Частично совместимыми являются суждения, которые могут быть одновременно истинными, но не могут быть одновременно ложными.
К подчиненным относятся такие суждения, в которых при истинности подчиняющего подчиненное всегда истинно.
Суждения, которые одновременно не могут быть истинными, являются несовместимыми.
Выделяют два вида несовместимости: 1) противоположность; 2) противоречие.
Противоположность – отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.
Противоречащими являются суждения, которые не могут быть одновременно истинными и ложными.
§ 4. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ
§ 4. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ
Сложные суждения, как и простые, могут быть сравнимыми и несравнимыми.
Сложные сравнимые суждения могут быть совместимыми и несовместимыми.
Отношение совместимости
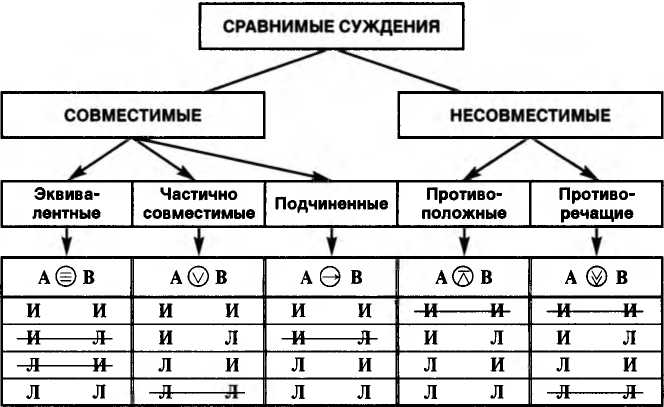
К совместимым относятся такие сравнимые суждения, которые одновременно могут быть истинными. В сложных суждениях, как и в простых, различают три вида совместимости: эквивалентность, частичная совместимость и подчинение.
1. Эквивалентные — это суждения, которые принимают одни и те же значения, т. е. одновременно являются либо истинными, либо ложными.
1-я и 4-я строки таблицы показывают, что А и В одновременно принимают одинаковые значения — И и Л; зачеркнутые 2-я и 3-я строки показывают, что эквивалентные суждения одновременно не могут принимать различные значения.
Отношение эквивалентности позволяет выражать одни сложные суждения через другие — конъюнкцию через дизъюнкцию или импликацию и наоборот. Приведем четыре известные эквивалентности, которые являются законами логики.
1) Выражение конъюнкции через дизъюнкцию:
2) Выражение дизъюнкции через конъюнкцию:
Эти две эквивалентности называются законами де Моргана.
3) Выражение импликации через конъюнкцию:
4) Выражение импликации через дизъюнкцию:
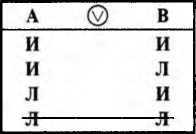
2. Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.
Отношение частичной совместимости для сложных суждений показано в таблице 9, где А и В — схемы сложных суждений; ? — знак частичной совместимости. 1-я строка таблицы говорит об одновременной истинности А и В; 2-я и 3-я — несовпадение значений; 4-я строка зачеркнута, поскольку исключается одновременная ложность А и В.
3. Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего подчиненное всегда будет истинным.
Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующею все виды рассуждений.
Отношение несовместимости
Несовместимыми являются суждения, которые одновременно не могут быть истинными. Это противоположность и противоречие.
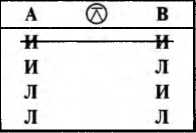
1. Противоположность — отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.
2. Противоречие — отношение между суждениями, которые одновременно не могут быть ни истинными, ни ложными. При истинности одного из них другое ложно, а при ложности первого второе истинно.
Вычеркнутые 1-я и 4-я строки показывают, что А и В могут принимать лишь альтернативные значения.
Обобщенная таблица логических отношений между сложными суждениями (таблица 13).
Сопоставление суждений в дискуссиях
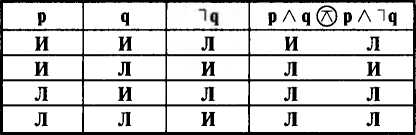
Отчетливое представление об отношениях, в которых могут находиться суждения, позволяет логически грамотно анализировать высказывания участников дискуссий. Бывают ситуации, когда логический анализ показывает совместимость различных по структуре суждений. Нередко это случается с частными суждениями. Пропонент утверждает, что «Некоторые S есть Р»; оппонент настаивает, что «Некоторые S не есть Р». На поверку же выходит, что эти суждения не исключают друг друга, а являются частично совместимыми и оба могут оказаться истинными.
В этом легко убедиться с помощью таблицы 14. Анализ показывает, что эти высказывания несовместимы, поскольку ни в одной строке не являются одновременно истинными. Вместе с тем они могут быть ложными (3-я и 4-я строки), значит, находятся в отношении противоположности. Отсюда следует, что если будет показана в целом несостоятельность утверждения обвинителя, то это еще не означает правоту защитника. Точно так же опровержение утверждений защитника логически не обязывает принимать точку зрения обвинителя. Может оказаться, что оба утверждения ложны и задача сведется к поиску нового объяснения фактам.
Вопросы для самопроверки
1. Какие сложные суждения являются несравнимыми и какие — сравнимыми?
2. На какие виды делятся сравнимые суждения?
3. На какие виды совместимости делятся сложные суждения?
4. Какие значения принимают эквивалентные отношения совместимости и несовместимости?
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
§ 5. Логические отношения между понятиями
§ 5. Логические отношения между понятиями Так как все предметы находятся во взаимодействии и взаимообусловленности, то и понятия, отражающие данные предметы, также находятся в определенных отношениях. Конкретные виды отношений устанавливаются в зависимости от
§ 6. Отношения между суждениями
§ 6. Отношения между суждениями Основу отношений между суждениями составляет их сходство по содержанию, выражаемое в таких логических характеристиках, как смысл и истинность суждений. В соответствии с этим логические отношения устанавливаются не между любыми, а лишь
Логические отношения между простыми атрибутивными суждениями
Логические отношения между простыми атрибутивными суждениями Так же, как и понятия, суждения могут быть сравнимыми и несравнимыми. Мы можем рассмотреть только сравнимые суждения. Сравнимыми называются суждения с одинаковыми субъектами и предикатами и различающиеся
2.8. Отношения между суждениями
2.8. Отношения между суждениями Простые суждения видов А, I, Е, О делятся на сравнимые и несравнимые. Сравнимые суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками, а несравнимые суждения имеют различные субъекты и предикаты. Например,
§ 6. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ
§ 6. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ Суждения делятся на сравнимые и несравнимые.Несравнимыми являются суждения, имеющие разные субъекты или предикаты. Таковы, например, два суждения: «Некоторые студенты первокурсники» и «Некоторые студенты
Глава III. Отношения между суждениями
Глава III. Отношения между суждениями Так же как и между понятиями, между суждениями существуют определенные логические отношения. Они тоже могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми. Но есть и принципиальное различие. Понятия, поскольку они ни
1. Отношения между простыми суждениями
1. Отношения между простыми суждениями Отношения между простыми суждениями определяются, с одной стороны, их конкретным содержанием, а с другой — логической формой: характером субъекта, предиката, логической связки.Поскольку по характеру предиката простые суждения
2. Отношения между сложными суждениями
2. Отношения между сложными суждениями Сложные суждения аналогично простым находятся в определенных отношениях между собой. Общим здесь является то, что они тоже могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми, причем и для них характерны отношения
3. Логические отношения между теориями
3. Логические отношения между теориями Если логические отношения существуют между понятиями и между суждениями, то вправе ли мы говорить о логических отношениях между теориями? Ведь это неизмеримо более сложные мыслительные конструкции! Да, вправе и именно потому, что
Глава III. Отношения между суждениями
Глава III. Отношения между суждениями 1. Отношения между простыми суждениями Сравнимые и несравнимые атрибутивные суждения1. Какие из следующих пар атрибутивных суждений являются сравнимыми, а какие — несравнимыми: «Земля — планета Солнечной системы» — «Луна —
1. Отношения между простыми суждениями
1. Отношения между простыми суждениями Сравнимые и несравнимые атрибутивные суждения1. Какие из следующих пар атрибутивных суждений являются сравнимыми, а какие — несравнимыми: «Земля — планета Солнечной системы» — «Луна — естественный спутник Земли». «Москва —
2. Отношения между сложными суждениями
2. Отношения между сложными суждениями Сравнимые и несравнимые сложные сужденияКакие из следующих сложных суждений — сравнимые, какие — не сравнимые: «Честь и выгода вместе не живут» — «Смерть и налоги неизбежны». «Честь и выгода вместе не живут» — «Выгода и честь
Глава III. Отношения между суждениями
Глава III. Отношения между суждениями § 1. Возможные логические отношения между суждениями Интерес логиков к структуре суждений вызван их желанием проявить все возможные формы суждений, с помощью которых суждения имплицируют друг друга. Помимо импликации суждения
§ 1. Возможные логические отношения между суждениями
§ 1. Возможные логические отношения между суждениями Интерес логиков к структуре суждений вызван их желанием проявить все возможные формы суждений, с помощью которых суждения имплицируют друг друга. Помимо импликации суждения могут быть связаны и другими отношениями.
Глава III. Отношения между суждениями
Глава III. Отношения между суждениями 1. Если суждение «все жирафы обладают длинной шеей» является истинным, что можно заключить относительно следующих суждений?a. Ни один жираф не обладает короткой шеей.b. Ни один жираф не обладает длинной шеей.c. Большинство жирафов
2. Отношения между сложными суждениями
2. Отношения между сложными суждениями
Сравнимые и несравнимые сложные суждения
Какие из следующих сложных суждений — сравнимые, какие — не сравнимые:
«Честь и выгода вместе не живут» — «Смерть и налоги неизбежны».
«Честь и выгода вместе не живут» — «Выгода и честь вместе не живут».
«Физические лица и должностные лица несут ответственность за нарушение таможенных правил» — «Неверно, что физические лица и должностные лица несут ответственность за нарушение таможенных правил».
Совместимые и несовместимые суждения
1. Приведите примеры совместимых сложных суждений.
2. В каких отношениях по истинности и ложности находятся такие суждения?
3. Приведите примеры несовместимых сложных суждений.
4. В каких отношениях по истинности и ложности находятся такие суждения?
Читайте также
§ 6. Отношения между суждениями
§ 6. Отношения между суждениями Основу отношений между суждениями составляет их сходство по содержанию, выражаемое в таких логических характеристиках, как смысл и истинность суждений. В соответствии с этим логические отношения устанавливаются не между любыми, а лишь
Логические отношения между простыми атрибутивными суждениями
Логические отношения между простыми атрибутивными суждениями Так же, как и понятия, суждения могут быть сравнимыми и несравнимыми. Мы можем рассмотреть только сравнимые суждения. Сравнимыми называются суждения с одинаковыми субъектами и предикатами и различающиеся
2.8. Отношения между суждениями
2.8. Отношения между суждениями Простые суждения видов А, I, Е, О делятся на сравнимые и несравнимые. Сравнимые суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками, а несравнимые суждения имеют различные субъекты и предикаты. Например,
§ 6. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ
§ 6. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ Суждения делятся на сравнимые и несравнимые.Несравнимыми являются суждения, имеющие разные субъекты или предикаты. Таковы, например, два суждения: «Некоторые студенты первокурсники» и «Некоторые студенты
§ 4. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СЛОЖНЫМИ СУЖДЕНИЯМИ
Глава III. Отношения между суждениями
Глава III. Отношения между суждениями Так же как и между понятиями, между суждениями существуют определенные логические отношения. Они тоже могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми. Но есть и принципиальное различие. Понятия, поскольку они ни
1. Отношения между простыми суждениями
1. Отношения между простыми суждениями Отношения между простыми суждениями определяются, с одной стороны, их конкретным содержанием, а с другой — логической формой: характером субъекта, предиката, логической связки.Поскольку по характеру предиката простые суждения
2. Отношения между сложными суждениями
2. Отношения между сложными суждениями Сложные суждения аналогично простым находятся в определенных отношениях между собой. Общим здесь является то, что они тоже могут быть сравнимыми и несравнимыми, совместимыми и несовместимыми, причем и для них характерны отношения
Глава III. Отношения между суждениями
Глава III. Отношения между суждениями 1. Отношения между простыми суждениями Сравнимые и несравнимые атрибутивные суждения1. Какие из следующих пар атрибутивных суждений являются сравнимыми, а какие — несравнимыми: «Земля — планета Солнечной системы» — «Луна —
1. Отношения между простыми суждениями
1. Отношения между простыми суждениями Сравнимые и несравнимые атрибутивные суждения1. Какие из следующих пар атрибутивных суждений являются сравнимыми, а какие — несравнимыми: «Земля — планета Солнечной системы» — «Луна — естественный спутник Земли». «Москва —
IV. О различии между аналитическими и синтетическими суждениями
IV. О различии между аналитическими и синтетическими суждениями Во всех суждениях, в которых мыслится отношение субъекта к предикату (я имею в виду только утвердительные суждения, так как вслед за ними применить сказанное к отрицательным суждениям нетрудно), это
Глава III. Отношения между суждениями
Глава III. Отношения между суждениями § 1. Возможные логические отношения между суждениями Интерес логиков к структуре суждений вызван их желанием проявить все возможные формы суждений, с помощью которых суждения имплицируют друг друга. Помимо импликации суждения
§ 1. Возможные логические отношения между суждениями
§ 1. Возможные логические отношения между суждениями Интерес логиков к структуре суждений вызван их желанием проявить все возможные формы суждений, с помощью которых суждения имплицируют друг друга. Помимо импликации суждения могут быть связаны и другими отношениями.
Глава III. Отношения между суждениями
Глава III. Отношения между суждениями 1. Если суждение «все жирафы обладают длинной шеей» является истинным, что можно заключить относительно следующих суждений?a. Ни один жираф не обладает короткой шеей.b. Ни один жираф не обладает длинной шеей.c. Большинство жирафов
IV. О различии между аналитическими и синтетическими суждениями
IV. О различии между аналитическими и синтетическими суждениями Во всех суждениях, в которых мыслится отношение субъекта к предикату (я имею в виду только утвердительные суждения, так как вслед за ними применить сказанное к отрицательным суждениям нетрудно), это
Логические отношения между сложными суждениями. Законы выразимости одних сложных суждений через другие.
Сложные суждения могут бытьсравнимыми и несравнимыми.
Несравнимые — это суждения, которые не имеют общих пропозициональных переменных. Сравнимые — это суждения, которые имеют одинаковые пропозиционные переменные и различаются логическими связками, включая отрицание. Например, сравнимыми являются следующие два суждения: «Норвегия или Швеция имеют выход в Балтийское море»
Сложные сравнимые суждения могут бытьсовместимыми и несовместимыми.
Отношение совместимости.
К совместимым относятся такие сравнимые суждения, которые одновременно могут быть истинными. Как и в случае простых суждений, различают три вида совместимости сложных суждений: эквивалентность, частичная совместимость и подчинение.
1. Эквивалентные — это суждения, которые принимают одни и те значения, т.е. одновременно являются либо истинными, либо ложными.
1) Выражение конъюнкции через дизъюнкцию:
2) Выражение дизъюнкции через конъюнкцию:
Эти две эквивалентности называются законами де Моргана.
3) Выражение импликации через конъюнкцию:
4) Выражение импликации через дизъюнкцию:
2. Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.
3. Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего подчиненное всегда будет истинным. Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчинённого, составляет основу фундаментального в науке логики понятия логического следования, регулирующего все виды рассуждений.
Отношение несовместимости.
Несовместимыми являются суждения, которые одновременно не могут быть истинными. Из двух видов несовместимости одна — противоположность, другая —противоречие.
Противоположность — отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.
Противоречие — отношение между суждениями, которые одновременно не могут быть ни истинными, ни ложными. При истинности одного из них другое будет ложным, а при ложности первого второе будет истинным.
Суждения, которыми мы оперируем, принимаются как логически значимые, т.е. как истинные или ложные, не произвольно, а в силу определенных оснований. Такими основаниями, обусловливающими принятие суждений, выступают либо структурно-логические характеристики самих суждений, либо их соотношение с фактическим положением дел в реальной действительности. Два способа обусловленности, или детерминированности суждений предопределяют соответствующие типы модальностей: 1) логическую модальность и 2) фактическую модальность.
Логическая модальность
Логическая модальность это логическая детерминированность суждения, истинность или ложность которого определяется структурой, или формой суждения.
К логически истиннымотносят суждения, выражающие законы логики; к логически ложным – внутренне противоречивые суждения.
Логически истинные суждения вместе с логически ложными образуют класс логически детерминированных суждений. Все остальные суждения, истинность или ложность которых не может быть определена исходя из их структуры, составляют класс фактически детерминированных суждений:
Фактическая модальность
Фактическая модальность связана с объективной, или физической детерминированностью суждений, когда их истинность и ложность определяются положением дел в реальной действительности. К фактически истинным относятся суждения, в которых связь между терминами соответствует реальным отношениям между предметами. Пример такого суждения: «Эйфелева башня находится в Париже». К фактически ложным относятся суждения, в которых связь между терминами не соответствует действительности. К примеру: «Ни одно млекопитающее не живет в воде».
Объективная устойчивость и интенсивность реальных связей между предметами находит свое выражение в фактической модальности суждений с помощью алетических модальных понятий необходимости и случайности.
Необходимость-случайность. Фактически необходимыми являются суждения, в которых содержится информация о законах науки. Например: «Сумма внутренних углов треугольника равна180°». В естественном языке такие суждения нередко выражают с помощью слов «необходимо», «обязательно», «непременно» и др. В логике для суждений необходимости принято выражение: «S необходимо есть (не есть) Р».
Суждения необходимости могут быть истинными, например: «Кислород необходим для поддержания жизни», но они могут быть и ложными, например: «Вода не кипит при 100С в нормальных условиях». Вместе они составляют класс фактически необходимых суждений. Все остальные фактические суждения относятся к случайным.
Модальные понятия «необходимость» и «случайность» могут быть эквивалентно выражены другой парой модальных понятий возможность и невозможность.
В естественном языке показателями суждений возможности являются слова: возможно, может быть, не исключается, допускается и другие, когда они употребляются в качестве сказуемых (а не вводных слов).
В логике для суждений возможности принято выражение «S может быть (может не быть) Р».
Дополнением к классу фактически возможных суждений является класс фактически невозможных суждений.
Фактически невозможными являются суждения, содержащие информацию о принципиальной несовместимости выраженных в субъекте и предикате явлений. Например: «На Луне невозможна жизнь»; «Невозможно чтобы в треугольнике сумма внутренних углов не была равна 180°»
По степени обоснованности среди знаний различают два непересекающихся класса суждений: достоверные и проблематичные.
1) Достоверные суждения – это достаточно обоснованные истинные или ложные суждения. Их истинность или ложность устанавливается либо путем непосредственной проверки, либо опосредованно, когда суждение подтверждается эмпирическими или теоретическими положениями.
Следует отметить, что в психологическом плане достоверное знание характеризуется отсутствием сомнений в истинности соответствующего суждения. Однако отсутствие сомнений само по себе еще не говорит о достоверности суждения, которое признается таковым при наличии соответствующих оснований – логических или эмпирических.
2)Проблематичные суждения – это суждения, которые нельзя считать достоверными в силу их недостаточности обоснованности. Поскольку истинность или ложность таких суждений точно не установлена, то они лишь претендуют быть таковыми. Отсюда и названия их: проблематичные, правдоподобные, или вероятные.
В естественном языке показателями проблематичности суждений обычно служат вводные слова: по-видимому, вероятно, представляется, возможно, можно предположить и др. Для проблематичных суждений принято выражение: «S, по-видимому, есть Р».
В судебном исследовании в форме проблематичных суждений строятся версии (гипотезы) об обстоятельствах расследуемых дел. Будучи обоснованными, правдоподобные суждения направляют расследование по правильному руслу и способствуют установлению по каждому делу достоверных результатов.
Если оператором Qобозначить уверенность субъекта S в истинности суждения р, то выражение в целом принимает вид QS(p) и читается: «S уверен в истинности р».