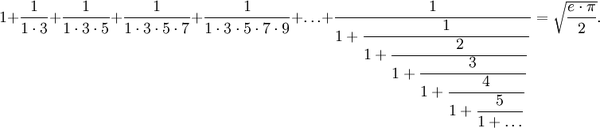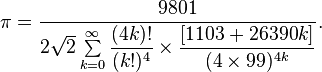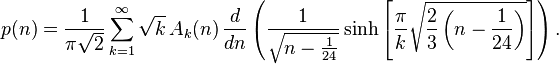отношение рода и вида в логике
Ч14. Родовые и видовые понятия.
Возьмём ряд понятий: «город» — «столица» — «Москва». Понятие «город» будет родовым по отношению к понятию «столица», а понятие «столица» будет родовым по отношению к понятию «Москва». Но эти же понятия находятся и в другом отношении: понятие «Москва» является видовым по отношению к понятию «столица», а понятие «столица» является видовым по отношению к понятию «город».
Таким образом, одно и то же понятие в одно и то же время может быть и видовым, и родовым, но только в разных отношениях: по отношению к менее общему — оно родовое, а по отношению к более общему — видовое.
Родовое понятие (или род) не может существовать отдельно от видовых понятий, а видовые понятия (или виды) не могут существовать отдельно от рода. Род и вид всегда взаимно связаны.
Эта взаимная связь рода и вида отражает существующую в предметах связь общего и отдельного, а именно: каждый предмет объективного мира содержит в себе и общие свойства, которые объединяют его с однородными предметами, и свои, особые свойства.
Например, яблоко есть плод (общее свойство, присущее яблокам и другим плодам), но яблоко имеет также свои, особые свойства, которых нет у других плодов; сосна есть дерево (общее свойство), но сосна имеет и свои, особые свойства, присущие только сосне и отличающие её от других деревьев.
Общие свойства существуют только в отдельных предметах. Тем самым общие свойства являются признаком отдельных предметов.
Так как всякое яблоко есть плод, то «плод» есть признак яблока; «дерево» есть признак сосны и т д. Причём эти общие свойства (плод, дерево) являются существенными признаками, так как они выражают коренные свойства предметов.
Точно так же родовые понятия, отражая объективную связь предметов и явлений действительности, являются признаками своих видов.
Когда мы говорим «химия есть наука», то мы указываем, к какому роду относится «химия» (к роду «наука»), и в то же время указываем существенный признак «химии», её родовой признак («наука»).
Наука vs религия
Заново пройти школьный курс
Всем привет. С недавнего времени всё больше понимаю, что в школе очень мало времени уделял таким важным наукам как химия и физика (в школе это казалось очень скучным). Поэтому не могли бы вы порекомендовать какие-нибудь книги по этой теме но написанные простым языком, в которых смогли уместить весь школьный курс, и было бы великолепно если при их прочтении не хотелось бы уснуть. Заранее спасибо.
Вот читаешь серьезные книжки, а там.
Как Обучается Искусственный Интеллект
Как все алгоритмы вокруг нас учатся выполнять свою работу?
В школе проявились его незаурядные способности к математике, и знакомый студент из города Мадраса дал ему книги по тригонометрии. В 14 лет Рамануджан открыл формулу Эйлера о синусе и косинусе и был очень расстроен, узнав, что она уже опубликована. В 16 лет в его руки попало двухтомное сочинение математика Джорджа Шубриджа Карра «Сборник элементарных результатов чистой и прикладной математики», написанное почти за четверть века до этого (впоследствии, благодаря связи с именем Рамануджана, эта книга была подвергнута тщательному анализу). В нём было помещено 6165 теорем и формул, практически без доказательств и пояснений. Юноша, не имевший ни доступа в вуз, ни общения с математиками, погрузился в общение с этим сводом формул. Таким образом, у него сложился определенный способ мышления, своеобразный стиль доказательств. В этот период и определилась математическая судьба Рамануджана.
В 1913 году известный профессор Кембриджского университета Годфри Харди получил письмо от Рамануджана, в котором Рамануджан сообщал, что он не заканчивал университета, а после средней школы занимается математикой самостоятельно. К письму были приложены формулы, автор просил их опубликовать, если они интересны, поскольку сам он беден и не имеет для публикации достаточных средств. Между кембриджским профессором и индийским клерком завязалась оживленная переписка, в результате которой у Харди накопилось около 120 формул, не известных науке. По настоянию Харди в 27-летнем возрасте Рамануджан переехал в Кембридж. Там он стал профессором университета, его выбрали в Лондонское королевское общество. Печатные труды с его формулами выходили один за другим, вызывая удивление, а подчас и недоумение коллег.
Годфри Харди:
В формировании математического мира Рамануджана начальный запас математических фактов объединился с огромным запасом наблюдений над конкретными числами. Он коллекционировал такие факты с детства. Он обладал поразительной способностью подмечать огромный числовой материал. По словам Харди, «каждое натуральное число было личным другом Рамануджана». Многие математики его времени считали Рамануджана просто экзотическим явлением, опоздавшим родиться на 100 лет. Не перестают удивляться проницательности индийского гения и математики нашего времени.
Одна из цепных дробей, найденных Рамануджаном:
Но самой известной его работой, совместная с профессором Харди, является работа по асимптотике разбиения натуральных чисел. То есть представление какого-либо натурального числа N в виде суммы других натуральных чисел.
Например, <3,1,1>или <3,2>— разбиения числа 5, поскольку 5 = 3 + 1 + 1 = 3 + 2. Всего существует p(5) = 7 разбиений числа 5: <1,1,1,1,1>, <2,1,1,1>, <2,2,1>, <3,1,1>, <3,2>, <4,1>, <5>.
Формула Харди-Рамануджана:
Сфера его математических интересов была очень широка. Это магические квадраты, квадратура круга, бесконечные ряды, гладкие числа, разбиения чисел, гипергеометрические функции, специальные суммы и функции, ныне носящие его имя, определённые интегралы, эллиптические и модулярные функции. + множество формул,теорем и равенств в теории чисел.
Сам Рамануджан говорил, что формулы ему во сне внушает богиня Намагири Тхайяр.
Умер в Мадрасском президентстве вскоре после возвращения в Индию. Причиной ранней (в возрасте 32 лет) смерти мог быть туберкулёз, усугубленный последствиями недоедания, истощения и стресса.
Отношения между понятиями
Урок 12. Информатика 4 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Отношения между понятиями»
Не успел я вас познакомить со своим приятелем Аркадием, он опять исчез. Каждый раз, когда я пытаюсь объяснить ему тему «Отношения между понятиями» происходит одно и тоже – Аркадий просто исчезает. Я понимаю, тема сложная, но неужели я так плохо объясняю?! А может это просто он ленится понимать.
Итак, знакомясь с этой темой, мы рассмотрим отношения между понятиями: «вид ↔ вид», «род → вид», «вид ← род».
Научимся узнавать и называть отношения. И будем строить схемы отношений в виде кругов Эйлера.
С профессором Знатоковым вы уже выясняли, что объекты реальной действительности находятся в определённых отношениях между собой. Например:
И знаете, что отношения между объектами бывают симметричными и несимметричными.
Так вот, понятия, так же, как и объекты, находятся в определённых отношениях между собой.
Давайте рассмотрим это на примере знаков. Знаки бывают разными: цифры, буквы, знаки препинания, знаки арифметических действий, иероглифы, дорожные знаки и другие.
Как мы помним, знак – это родовое понятие. А цифра, буква, знак препинания, знак арифметических действий, иероглиф, дорожный знак – это видовые понятия.
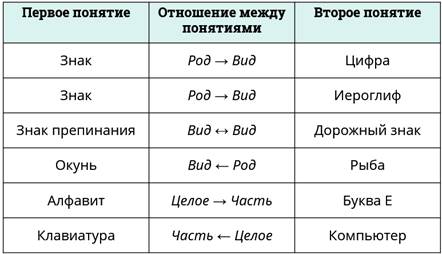
Давайте рассмотрим отношения между понятиями в таблице.
В первом столбце запишем первое понятие. В третьем столбце – второе понятие. А во втором – отношение между этими понятиями.
Итак, первая пара понятий: знак, цифра. Знак – это родовое понятие, цифра – это видовое понятие. Значит, отношение род → вид.
Вторая пара понятий: знак, иероглиф. Знак – это родовое понятие, иероглиф – это видовое понятие. Отношение опять род → вид.
Следующая пара: знак препинания, дорожный знак. Оба эти понятия относятся к видовому понятию. Значит, отношение между ними вид ↔ вид.
Пара отношений: окунь, рыба. Окунь – это видовое понятие, рыба – родовое. Значит, отношение вид ← род.
Мы получили отношения: род → вид, вид ↔ вид и вид ← род. Ещё между понятиями могут быть и другие отношения, такие как: целое → часть и часть ← целое.
Помните, между объектами тоже встречались такие отношения?
Вот пара понятий: алфавит, буква Е. Алфавит, конечно, это целое, а буква Е – часть. Значит отношение между ними целое → часть.
Клавиатура, компьютер. Отношение между ними часть ← целое.
Обратите внимание на то, что линия со стрелкой начинается от отношений «род» и «целое» и указывает на отношения «вид» и «часть».
Отношения между понятиями бывают несимметричными и симметричными.
Ребята, запомните, что несимметричные отношения обозначают однонаправленной стрелкой, а симметричные – двунаправленной стрелкой.
Симметричные отношения – это отношения между понятиями одного уровня. Например, между видовыми понятиями.
Давайте рассмотрим вот такую схему и расставим в ней отношения между понятиями в виде стрелок.
Между понятиями «знак» и «буква» отношение род → вид, стрелка одностороння и направлена от родового понятия к видовому. Между понятиями «знак» и «цифра» всё аналогично.
«Буква» и «цифра» – понятия одного уровня, поэтому отношение между ними симметричное вид ↔ вид и стрелка двусторонняя. Такое же симметричное отношение и между понятиями «буква Л» и «буква Д» и «цифра 7» и «цифра 3».
А вот отношение между понятиями «буква» и «Буква Л» и «буква» и «Буква Д» несимметричное род → вид.
Тоже самое можно сказать и про отношения между понятиями «цифра» и «цифра 7» и «цифра» и «цифра 3».
Я читал, что если понятия при симметричных отношениях поменять местами, то название отношения не изменится. Давайте проверим, так ли это.
Поменяем буквы местами между собой, а цифры. Отношения не изменились, как были симметричные, так и остались.
А если поменять вот так тоже всё по-прежнему. Между понятиями «цифра» и «буква» отношение симметричное.
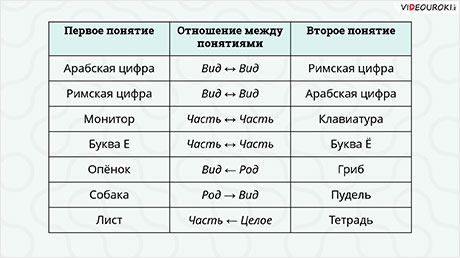
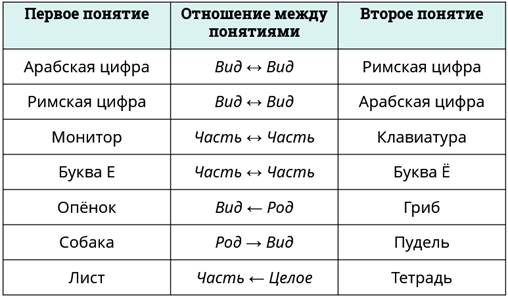
Предлагаю сейчас закрепить полученные знания, дописав в таблицу отношения между предложенными понятиями.
В первой паре понятий «арабская цифра», «римская цифра» отношения вид ↔ вид.
Во второй паре понятий «римская цифра», «арабская цифра» отношения вид ↔ вид. Как мы уже сказали, если понятия при симметричных отношениях поменять местами, то название отношения не изменится.
Следующая пара «монитор», «клавиатура». А вот тут надо быть внимательным. И монитор, и клавиатура – это часть от целого «компьютера». В данном случае отношение между понятиями часть ↔ часть.
В следующей паре отношение между понятиями тоже часть ↔ часть.
В этой паре отношение между понятиями вид ← род.
Между понятиями «собака», «пудель» отношение род → вид.
И последняя пара понятий «лист», «тетрадь» отношение часть ← целое.
Есть и другие виды отношений между понятиями. Например, отношение пересечения понятий.
Давайте сразу рассмотрим на примере.
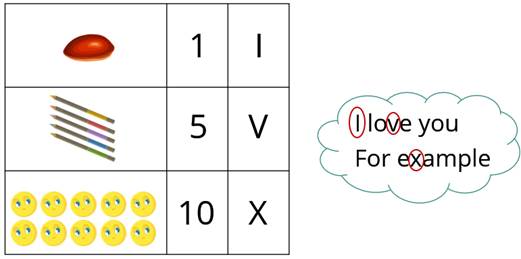
Изображён один пирожок. Обозначим количество пирожков, используя арабские цифры и римские цифры.
Вот изображено пять карандашей.
Десять смайликов также арабскими цифрами и римскими.
У меня такое ощущение, что эти римские цифры я не раз видел не в качестве цифр, а в качестве букв. Ну, да!
Смотрите, ребята, что получается, некоторые латинские буквы используются в качестве римских цифр.
Поэтому мы смело можем сказать, что понятие «буква» и понятие «цифра» находятся в отношении пересечения. Такое отношение удобно изображать наглядной схемой – кругами Эйлера.
Вот круг, который обозначает понятие «буква», а вот круг, обозначающий понятие «цифра». И эти оба круга пересекаются. А ещё они находятся внутри большого круга «знак».
Глядя на круги Эйлера, мы можем сказать, что понятия «буква» и «цифра» входят в понятие «знак».
Кругами Эйлера можно изобразить и непересекающиеся понятия. Например, понятия «компьютер» и «человек». Они не пересекаются, так как ни один компьютер не является человеком и не один человек не является компьютером в современном понимании этого слова.
Круги Эйлера – это наглядное и удобное представление отношений между двумя или несколькими понятиями. Размер кругов Эйлера может быть любым: маленьким или большим, не имеет значение. Главное, чтобы были правильно представлены отношения между понятиями. Круг, который обозначает видовое понятие, должен быть меньше и входить в другой круг большего размера, который обозначает родовое понятие.
А сейчас выполним небольшое задание.
Представьте с помощью кругов Эйлера отношения между понятиями «носитель информации», «бумага», «камень» и отношения между понятиями «двузначное число», «чётное число», «натуральное число».
В первой группе слов отношения между понятиями выглядят вот так.
Понятия «бумага» и «камень» входят в понятие «носитель информации». «Бумага» и «камень» – это непересекающиеся понятия.
Отношения между понятиями во второй группе выглядят так.
Понятия «двузначное число» и «чётное число» входят в понятие «натуральное число».
Понятие «двузначное число» и понятие «чётное число» находятся в отношении пересечения. Ведь некоторые двузначные числа являются чётными числами.
Итак, какие же итоги можно подвести из нашего урока.
Отношения между понятиями бывают род → вид, вид ↔ вид, вид ← род, целое → часть, часть ← целое и часть ↔ часть.
Отношения могут быть симметричными и несимметричными. Отношения между видовыми понятиями одного уровня (вид ↔ вид) – симметричные. Отношения между родовым и видовым понятиями (род → вид и вид ← род) – несимметричные.
Круги Эйлера помогают наглядно представить информацию об отношениях между понятиями.
Логика. Учебник для средней школы.
Глава III
ПОНЯТИЕ
§ 5. Соотношение между содержанием и объёмом понятия
Между содержанием и объёмом понятия существует определённое соотношение. Рассмотрим это соотношение на примере.
В объём понятия «позвоночные» входят все виды позвоночных животных, а содержанием являются существенные признаки, общие для всех позвоночных. Возьмём понятие, меньшее по объёму: «млекопитающие». В объём этого понятия входят не все виды позвоночных, а только часть их, следовательно, объём понятия будет меньше.
Однако содержание понятия расширяется за счёт новых признаков. Понятие «млекопитающие» содержит в себе признаки позвоночных (всякое млекопитающее есть позвоночное), а кроме того, оно содержит ещё свои, особые признаки (кормление детёнышей молоком и др.), которых не было в содержании понятия «позвоночные».
Другой пример: всякая берёза есть дерево, следовательно, понятие «берёза» содержит в себе все признаки понятия «дерево». Но берёза имеет ещё и свои, особые признаки, следовательно, в содержании понятия «берёза» признаков больше, чем в содержании понятия «дерево». Однако по объёму понятие «берёза» уже, чем понятие «дерево».
Итак, понятия, более широкие но объёму, являются более узкими по содержанию — такова зависимость между содержанием и объёмом понятий. Эта зависимость имеет значение закона, который называется законом обратного отношения содержания и объёма понятий. Формулировка закона следующая:
чем шире содержание понятия, тем уже его объём. И соответственно наоборот: чем уже содержание понятия, тем шире его объём.
Закон «обратного отношения» распространяется только на такие понятия, из которых одно входит в объём другого.
Однако из данного закона не следует, что более широкие по объёму, т. е. более общие, понятия имеют для нас меньшую ценность. Общие понятия отображают общие свойства, связи и закономерности предметов и явлений объективного мира.
§ 6. Ограничение и обобщение понятия
В практике мышления мы нередко пользуемся логическими приёмами, которые называются обобщением понятия и ограничением понятия.
Обобщить понятие — это значит перейти от менее общего к более общему понятию.
Ограничить понятие — это значит перейти от более общего понятия к менее общему понятию.
В соответствии с этим (согласно «закону обратного отношения») изменяется содержание понятия.
Рассмотрим процесс ограничения понятия на следующем примере. Объяснение того, что такое натрий, можно начать с напоминания о том, что представляет собой вообще элемент, а затем в понятие «элемент» ввести некоторые признаки, свойственные металлу. Введение этих признаков сузит объём понятия «элемент», ограничит объём этого понятия, тем самым получится другое понятие, с меньшим объёмом, — понятие «металл».
Далее, вводя в понятие «металл» признаки, свойственные натрию, мы тем самым ограничиваем понятие «металл», т. е. даём вместо него ещё менее общее понятие — «натрий».
Таким образом, процесс ограничения понятия представляет собой постепенный переход от более общих понятий к менее общим.
Ограничением понятий мы пользуемся в тех случаях, когда разъясняем содержание какого-либо понятия, причём строим своё разъяснение на основе уже известных, более общих понятий.
Ограничение понятия применяется также в тех случаях, когда бывает необходимо уточнить содержание понятия, указать, к какому именно кругу явлений относится данное понятие, следовательно, отграничить понятие от других понятий, в том числе и от более общих.
В процессе ограничения понятий, переходя от более общих понятий к менее общим, мы приходим, наконец, к таким понятиям, объём которых равен единице и которые, следовательно, не могут подлежать дальнейшему ограничению. Такие понятия отражают единичные, индивидуальные предметы и являются предельно узкими по объёму.
Примеры таких понятий: «Каспийское море», «первая мировая война 1914 года», «улица Горького в Москве».
Обобщение понятия представляет собой процесс, обратный ограничению. При обобщении понятия путём исключения некоторых его признаков мы переходим от менее общих ко всё более и более общим понятиям. Например, от понятия «чех» — к понятию «славянин», от понятия «славянин» — к понятию «человек».
Процесс обобщения понятия протекает на основе того, что круг рассматриваемых нами предметов всё более и более расширяется за счёт новых, отличных по своим свойствам предметов.
Обобщая понятия, переходя от менее общих к более общим, мы приходим, наконец, к предельно широким по объему понятиям, которые не подлежат дальнейшему обобщению.
Примеры категорий: «материя», «время», «движение», «пространство», «количество», «форма» и др.
§ 7. Родовые и видовые понятия
Возьмём ряд понятий: «город» — «столица» — «Москва». Понятие «город» будет родовым по отношению к понятию «столица», а понятие «столица» будет родовым по отношению к понятию «Москва». Но эти же понятия находятся и в другом отношении: понятие «Москва» является видовым по отношению к понятию «столица», а понятие «столица» является видовым по отношению к понятию «город».
Таким образом, одно и то же понятие в одно и то же время может быть и видовым, и родовым, но только в разных отношениях: по отношению к менее общему — оно родовое, а по отношению к более общему — видовое. В приведённом выше примере понятие «столица» является видовым по отношению к понятию «город» и родовым по отношению к понятию «Москва».
Родовое понятие (или род) не может существовать отдельно от видовых понятий, а видовые понятия (или виды) не могут существовать отдельно от рода. Род и вид всегда взаимно связаны.
Эта взаимная связь рода и вида отражает существующую в предметах связь общего и отдельного, а именно: каждый предмет объективного мира содержит в себе и общие свойства, которые объединяют его с однородными предметами, и свои, особые свойства.
Например, яблоко есть плод (общее свойство, присущее яблокам и другим плодам), но яблоко имеет также свои, особые свойства, которых нет у других плодов; сосна есть дерево (общее свойство), но сосна имеет и свои, особые свойства, присущие только сосне и отличающие её от других деревьев.
Общие свойства существуют только в отдельных предметах. Тем самым общие свойства являются признаком отдельных предметов.
Так как всякое яблоко есть плод, то «плод» есть признак яблока; «дерево» есть признак сосны и т д. Причём эти общие свойства (плод, дерево) являются существенными признаками, так как они выражают коренные свойства предметов.
Точно так же родовые понятия, отражая объективную связь предметов и явлений действительности, являются признаками своих видов.
Когда мы говорим «химия есть наука», то мы указываем, к какому роду относится «химия» (к роду «наука»), и в то же время указываем существенный признак «химии», её родовой признак («наука»).
§ 8. Основные классы понятий
По своему объёму понятия делятся на единичные и общие.
Единичные понятия являются понятиями об отдельных (единичных) предметах.
Примерами таких понятий могут быть следующие: «полководец М. И. Кутузов», «город Ленинград», «Народно-Демократическая Республика Болгария», «самое глубокое озеро в мире».
В общих понятиях отображается множество однородных предметов.
Например: «звезда», «книга», «школа», «песня», «урожай» и др.
Каждое из этих понятий относится к большой группе однородных предметов.
Общие понятия могут быть более общими и менее общими. Так, понятие «трактор» является менее общим по отношению к понятию «сельскохозяйственная машина», но более общим по отношению к понятию «гусеничный трактор».
Число предметов, которые охватываются общим понятием, может быть ограниченным или неограниченным. Например, общее понятие «корабль» относится ко всем кораблям, которые были, есть и будут.
К общим понятиям с ограниченным объёмом относятся такие понятия: «станции Московского метро первой очереди», «произведения Лермонтова», «учёные XIX века».
Общие и единичные понятия могут быть собирательными понятиями.
Собирательные понятия — это такие понятия, в которых мыслится совокупность однородных предметов как единое целое.
Например: «лес» (деревьев), «библиотека» (книг), «собрание» (учеников).
Особенность собирательных понятий заключается в том, что их нельзя приложить к отдельным предметам, совокупность которых мыслится в данном собирательном понятии. Нельзя, например, отнести понятие «лес» к отдельному дереву, понятие «собрание» к отдельному ученику.
Собирательные понятия можно приложить или к совокупности предметов как единому целому, или к ряду таких совокупностей. В первом случае будет единичное собирательное понятие, во втором случае — общее собирательное понятие.
Например, понятие о Государственной библиотеке имени В. И. Ленина в Москве будет единичным собирательным понятием, а понятие о библиотеке (вообще) будет общим собирательным понятием, так как оно относится ко многим библиотекам.
Примеры общих собирательных понятий: «группа», «созвездие», «коллектив», «полк», «народ», «толпа», «класс» и др. Примеры единичных собирательных понятий: «созвездие Большая Медведица», «коллектив служащих (такого-то) учреждения», «рабочий класс демократической Польши».
Каждое понятие находится в различных отношениях с другими понятиями и поэтому одновременно входит в разные классы.
Например, понятие «высота» есть общее, несобирательное; понятие «собрание» — общее, собирательное; понятие «единство стиля и содержания в рассказах А. П. Чехова» — единичное, собирательное.