отношение площадей треугольников с общим углом
Отношение площадей треугольников с общим углом
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.<1>^<○>$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
$$ 2.<2>^<○>$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
$$ 2.<3>^<○>$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC
DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
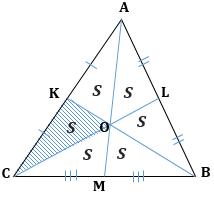
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
2. Через точку `D` проведём прямую `DL«|\|«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«|\|«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«|\|«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
| `S_(m_am_bm_c)=3/4S_(abc)`. |
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
Основные свойства площадей треугольников
Факт 1.
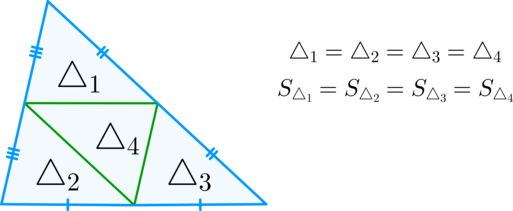
\(\bullet\) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
Факт 2.
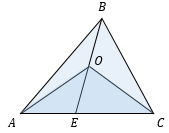
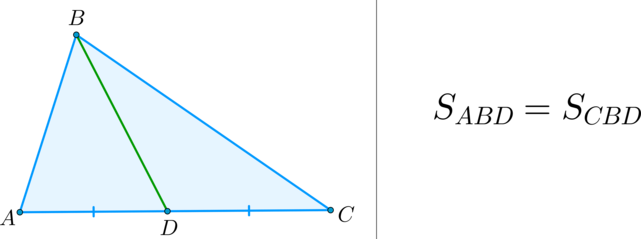
\(\bullet\) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
\(\bullet\) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
Факт 4.
\(\bullet\) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Факт 5.
\(\bullet\) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
\(\bullet\) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
Факт 7.
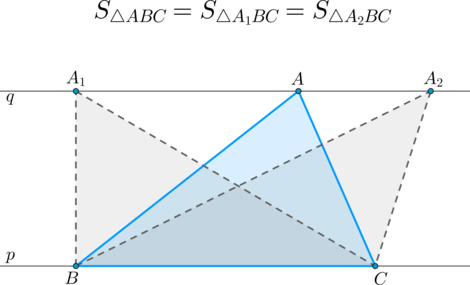
\(\bullet\) Если прямые \(p\) и \(q\) параллельны, то
Факт 8.
\(\bullet\) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
\(\bullet\) Отношение периметров подобных треугольников равно коэффициенту подобия.
51. Планиметрия  Читать 0 мин.
Читать 0 мин.
51.506. Отношения
Зачастую в геометрических задачах в условии даются отношения отрезков и площадей или отношение отрезков нужно найти. Существует ряд теорем и свойств фигур и их элементов, в которых так или иначе используются отношения.
ОТНОШЕНИЯ ОТРЕЗКОВ:
1. Все медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины: AO : AM = 2 : 1.
4. Диагонали параллелограмма точкой пересечения делятся пополам.
Произвольный параллелограмм или ромб:
Прямоугольник или квадрат:
ОТНОШЕНИЯ ПЛОЩАДЕЙ:
2. Треугольник делится тремя медианами на шесть равновеликих треугольников:
ЛЕММЫ О ПЛОЩАДЯХ ТРЕУГОЛЬНИКА:
Площади подобных фигур относятся как квадрат коэффициента подобия.
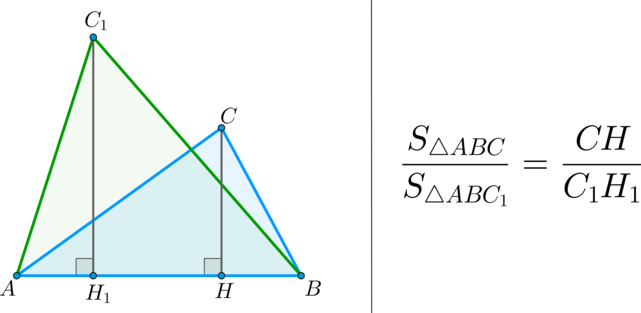
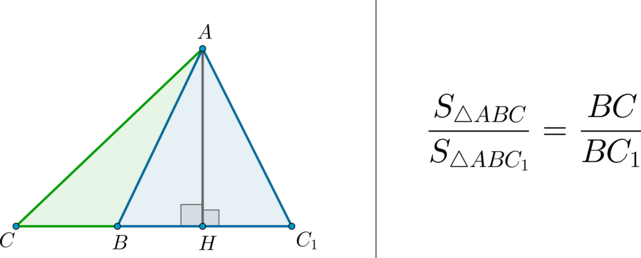
Если стороны треугольников с общей вершиной лежат на одной прямой, то их площади относятся как основания.
Если два треугольника имеют общую сторону, то их площади соотносятся как длины отрезков BE и OE.
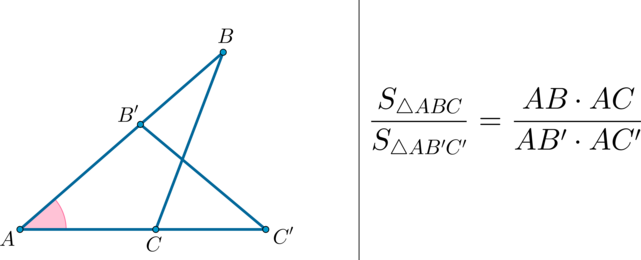
Если два треугольника имеют общий угол, то их площади соотносятся как произведения соответствующих сторон, прилежащих к этому углу.
Лемма 4 применима даже в том случае, если точки нового треугольника были взяты не на сторонах, а на продолжениях сторон. Пусть точка Е лежит на продолжении стороны AB за вершину В.
Теорема об отношении площадей треугольников, имеющих по равному углу. 8-й класс
Класс: 8
Презентация к уроку
Девиз урока: «Дорогу осилит идущий, а математику – мыслящий»
Тип урока: урок изучения нового материала.
Цели урока:
обучающие:
а) повторение основного теоритического материала;
б) рассмотрение основных задач на вычисление площадей треугольников;
в) доказательство теоремы об отношении площадей треугольников, имеющих по равному углу;
г) закрепление навыков решения в процессе самостоятельного разбора задач.
развивающие:
а) развитие умения планировать полный или частичный ход решения;
б) развитие умения осуществлять целенаправленные поисковые действия умственного плана;
в) развитие интереса к предмету;
г) развитие умения осуществлять самоконтроль.
воспитательные
б) воспитание умения слушать и слышать товарища.
Ход урока
I. Мотивация к учебной деятельности и постановка целей урока.
Учитель приветствует учащихся, поверяет их готовность к уроку, сообщает тему урока, формулирует цели урока. Слайды 1, 2
II. Повторение и актуализация необходимых знаний.
Один ученик готовит теоретический вопрос: сформулировать и доказать теорему о площади треугольника. Один ученик решает задачу у доски.
Рис. 1. Чертеж к условиям задачи
4 ученика получают задание на карточке (Карточки 2, 3). Остальные учащиеся решают устно по готовым чертежам.
Устно. Слайд 3. 1. Найдите площадь треугольника ABC.
Рис. 2. Чертеж к задаче 1
Слайд 4. 2. Дано: ABCD – квадрат, AB = 5 см, KD = 4 см.
Рис. 3. Чертеж к задаче 2
Слайд 5. 3. Найдите площадь треугольника ABC.
Рис. 4. Чертеж к задаче 3
Слайд 6. 4. BC = 6см, AC = 8см, AB = 10см.
Рис. 5. Чертеж к задаче 4
Рис. 6. Чертеж к условию задачи 5
Рис. 7. Теорема о площади треугольника
Слайд 7. Теорема. Площадь треугольника равна половине произведения основания на высоту, проведённую к этой стороне.
Учитель и учащиеся слушают теорему и её доказательство, проверяют решение задачи.
Учитель собирает у 4 учащихся листы с решением задач.
III. Создание проблемной ситуации и формулирование проблемы
Рис. 8. Свойство площадей треугольников, имеющих общую высоту
Слайд 8. Если высоты треугольников равны, то площади относятся как основания.
Рис. 9. Свойство медиан треугольника
Слайд 9. Медиана делит треугольник на два равновеликих треугольника. Три медианы делят треугольник на 6 равновеликих треугольников.
Слайд 10. 1. Решите задачу:
Рис. 10. Чертеж к условию задачи 1
Найти:
Какую часть площадь одного треугольника составляет от площади другого?
Или. Во сколько раз площадь одного треугольника больше (меньше) площади другого?
Слайд 11. 2. Решите задачу:
Рис. 11. Чертеж к условию задачи 2
Дано: ABCD – выпуклый четырёхугольник.
Вопрос: Как относятся площади треугольников, имеющих по равному углу?
IV. Изучение новой темы
Слайд 12. Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведение сторон, заключающих равные углы.
Рис. 12. Теорема о соотношении площадей треугольников, имеющих равный угол
V. Первичное закрепление
Учитель на экране показывает задачи, учащиеся предлагают свои решения задач
Слайд 14. Запишите отношение площадей
Рис. 14. Чертеж к пункту а) Рис. 15. Чертеж к пункту б)
Рис. 16. Чертеж к условию задачи
Рис. 17. Чертеж к условию задачи
VI. Самостоятельная работа
Учитель раздаёт карточки с заданиями двух уровней сложности. (Приложение 2)
Карточка. Уровень А
1) Две стороны треугольника равны 12 см и 9 см, угол между ними 30°. Найдите площадь треугольника. (Ответ: 27 см 2 )
Рис. 18. Чертеж к условию задачи
Уровень Б (для более подготовленных учащихся)
1) В треугольнике ABC ∠A = 45°, BC = 10 см, высота BD делит сторону AC на отрезки: AD = 6 см, DC = 8 см. Найдите площадь треугольника ABC и высоту, проведённую к стороне BC.
Рис. 19. Чертеж к условию задачи
Ответ: 42 см 2 ; 8,4 см.
Рис. 20. Чертеж к условию задачи
VII. Подведение итогов
Учитель оценивает работу учащихся.
VIII. Домашнее задание (Приложение 3)
Учебник. Учить теорему п. 52. № 479 (а).
Рис. 21. Чертеж к условию задачи
Дано: AO = AB, прямая AC параллельна прямой BD.
Рис. 22. Чертеж к условию задачи
Дано: AO = 3 см, BO = 6 см, CO = 5 см, DO = 4 см.
Литература:
Отношение площадей треугольников, имеющих равный угол
Ищем педагогов в команду «Инфоурок»
Конспект урока по геометрии в 8-м классе
«Отношение площадей треугольников, имеющих равный угол»
Булаева Валентина Егоровна, учитель математики
Тип урока: урок изучения нового материала.
сформулировать и доказать теорему об отношении площадей треугольников, имеющих один равный угол;
рассмотреть применение теоремы при решении задач на нахождение площадей многоугольников;
продолжить формирование умений и навыков решения задач на нахождение площадей многоугольников.
развивать интуицию, умения анализировать условие задачи, логически мыслить, обобщать полученные результаты;
развивать навыки правильной математической речи.
воспитывать аккуратность при выполнении чертежей и оформлении решения задач;
воспитывать самостоятельность и самоконтроль.
Оборудование для урока:
компьютер с программой просмотра презентаций;
рабочие тетради к учебнику Атанасяна у всех учащихся.
I. Организационный момент.
Сообщается тема урока, формулируются его цели.
II. Актуализация знаний учащихся.
Устный опрос (фронтальная работа с классом).
Ответьте на вопросы:
– Какие фигуры называются равносоставленными?
– Как называются фигуры, имеющие равную площадь?
– Верно ли, что равные фигуры имеют равные площади?
– Верно ли, что равносоставленные фигуры имеют равные площади?
– Верно ли, что разные фигуры имеют равные площади?
– В треугольнике АВС АВ = 3АС. Чему равно отношение высот треугольника, проведенных из вершин В и С?
– Катеты прямоугольного треугольника 6 см и 8 см. Длина гипотенузы 10 см. Вычислите высоту, проведенную к гипотенузе.
– Дана трапеция АВСD с основаниями АВ и СD. Докажите, что:
а) треугольники АВD и ВАС имеют равные площади;
б) треугольники АОD и ВОС имеют равные площади;
В треугольнике АВС проведена медиана ВD. Во сколько раз площадь треугольника АВD меньше площади треугольника АВС? Объясните.
Проверка домашнего задания.
Задача № 40 рабочей тетради. Один учащийся читает решение по своей тетради, остальные обсуждают и проверяют.
Треугольники ABM и ABC имеют общую высоту BD, поэтому их площади относятся как основания АМ и МС. Так как по условию AM : МС = 2 : 3, то AM : АС = 2 : 5 и
Далее проверяется дополнительная задача. Ее решение предлагается воспроизвести одному из учащихся, справившихся с этой задачей.
Высоты треугольников ВСЕ и АВС равны, тогда
Высоты треугольников BEM, MEH, CEH равны, их площади относятся так же, как
ВМ : МН : СН, т.к. ВМ = МН = СН, то S BEM = S MEH = S CEH =
III. Изучение нового материала.
Постановка проблемной задачи.
Рассмотрим решение следующей задачи рабочей тетради № 41.
Площади каких треугольников рассматриваются? Можно ли применить к решению задачи общую формулу площади треугольника или отношение площадей треугольников с равными высотами?
Есть ли у рассматриваемых треугольников равные элементы?
Итак, наша цель – выяснить, как связаны площади треугольников, имеющих по равному углу.
Формулирование и доказательство теоремы.
Теорема: Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, заключающих равные углы.
Анализируем условие теоремы.
– Сформулируйте что дано в данной теореме: сколько треугольников рассматривается, какое условие накладывается на них?
Записываем условие теоремы:
– Сформулируйте заключение данной теоремы.
– Что называется отношением двух величин?
– О каких отношениях идет речь в теореме?
Записываем заключение теоремы:
Наложим один треугольник на другой так, чтобы равные углы А и А 1 совпали, сторона А 1 В 1 лежала на луче АВ, а сторона А 1 С 1 на луче АС.
Рассмотрим два треугольника
– Что общего у этих треугольников?
– Чему равно отношение площадей треугольника с равными высотами?
–
– Запишите соответствующее равенство:
Рассмотрим другие два треугольника
– Что общего у этих треугольников?
– Чему равно отношение площадей треугольника с равными высотами?
– Запишите соответствующее равенство:
Перемножим равенства (1) и (2):
IV. Закрепление изученного материала.
Устное решение задач по готовым чертежам.
Решение задач с записью в тетради.
№ 3. Площадь одного равностороннего треугольника в 3 раза больше, чем площадь другого равностороннего треугольника. Найдите сторону второго треугольника, если сторона первого равна 1.
Подытожить, что изучали на данном уроке, оценить работу учащихся
VI. Домашнее задание.
п. 52, № 41 рабочей тетради, № 479 учебника.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДВ-040197
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
В Иркутской области продлили школьные каникулы
Время чтения: 1 минута
Кабмин утвердил список вузов, в которых можно получить второе высшее образование бесплатно
Время чтения: 2 минуты
Вузам Москвы и Подмосковья рекомендовали с 8 ноября ввести смешанный формат обучения
Время чтения: 1 минута
Роспотребнадзор продлил действие санитарных правил для школ
Время чтения: 1 минута
Рособрнадзор открыл горячую линию по вопросам контрольных в школах
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.


 Читать 0 мин.
Читать 0 мин.