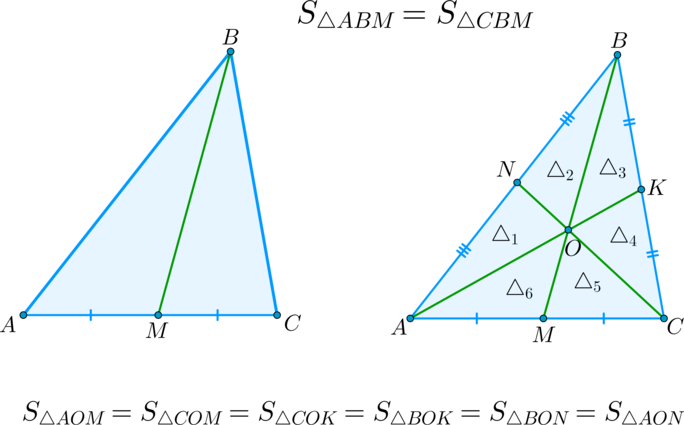
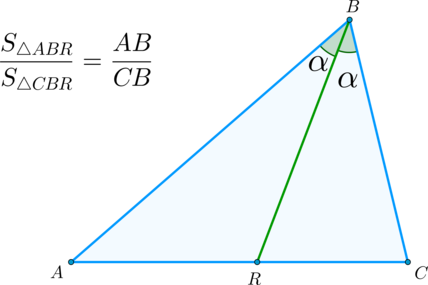
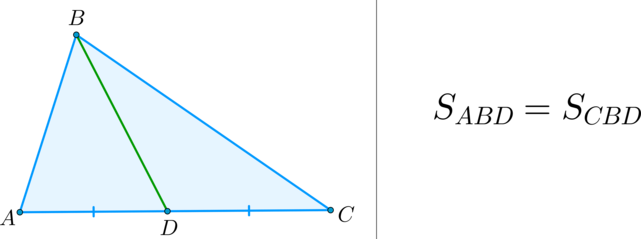
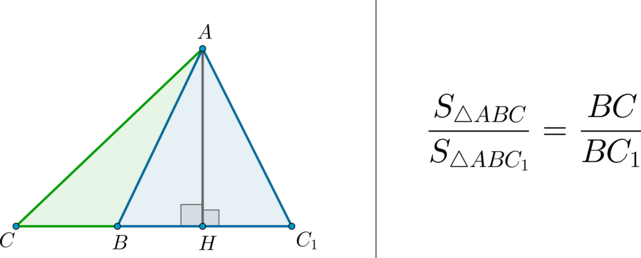
отношение площадей равно отношению оснований
Отношение площадей треугольников, имеющих общую высоту (основание)
Разделы: Математика
Ход урока
1. Организационный момент
Сообщаем тему урока. Поясняем важность рассматриваемого на уроке материала, говорим о том, что сведения последних уроков по площадям имеют широкое применение, сегодня на уроке используем их при решении задач.
Для эффективности работы в начале проверим домашнее задание и повторим изученный теоретический материал.
2. Проверка домашнего задания
В это время с классом работаем устно, по слайдам заранее подготовленной презентации.
3) Если AM=MC, то сравните площади этих треугольников.
Записать вывод в тетрадь:
Медиана делит треугольник на два равновеликих (равных по площади) треугольника, и площадь каждого из которых равна половине площади данного треугольника.
ВМ – медиана 
ВК – медиана 
Найдите отношение площадей
5) Известно, что SABС=20см 2 (по условию предыдущего задания)
Чему равно отношение площадей двух треугольников, имеющих общее основание?
Записываем вывод в тетради:
Площади треугольников, имеющих общее основание, относятся как высоты, проведенные к основанию.
Далее заслушиваем и обсуждаем теоретические ответы учащихся по ДЗ.
3. Закрепление ранее изученного материала.
1. Выполняем задание №40 стр. 18-19 рабочей тетради по геометрии для 8 кл.
На рисунке точка М делит сторону АС 
2. Решаем задачу №475 учебника.
Начертите 
Обсуждаем решение, используя слайды презентации
4. н/о (если позволяет время)
Данный параллелограмм разделите на три равновеликие части прямыми, выходящими из одной вершины.
Аналогично, ВВ2 делит 
4. Самостоятельная работа обучающего характера
1) СК – медиана 
На стороне КМ отмечена точка А так, что КА : АМ = 2 :3
1) АМ – медиана 
Найти площадь 
На стороне DК отмечена точка А так, что DА : АK = 3 :1
5. Постановка домашнего задания
Д.З. по учебнику стр. 124-125 № 473; 506; 511(а)
6. Подведение итогов урока
Литература
1. Геометрия 7-9. / Л.С. Атанасян, В.Ф. Бутузов и др./ “ Просвещение”, ОАО “Московский учебник”,М., 2008;
2. Рабочая тетрадь для 8 кл. об/об учреждений. Геометрия. / Атанасян Л.С. и др. / “Просвещение”, М, 2005;
2. Полонский В.Б., Рабинович Е.М., Якир М.С. / Геометрия: Задачник к школьному курсу М.: АСТ-ПРЕСС: Магистр-S, 1998.
Отношение площадей равно отношению оснований
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
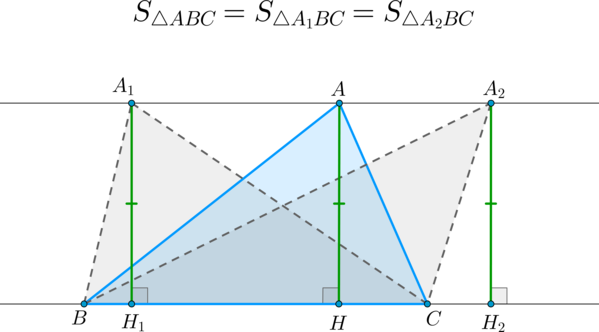
$$ 2.<1>^<○>$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
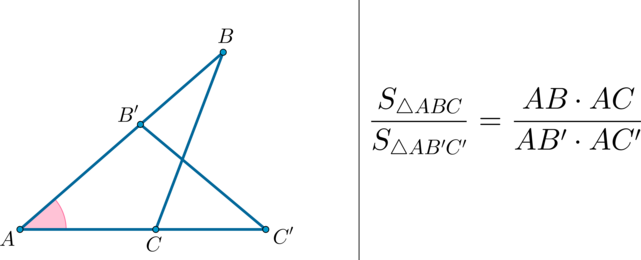
$$ 2.<2>^<○>$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
$$ 2.<3>^<○>$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC
DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
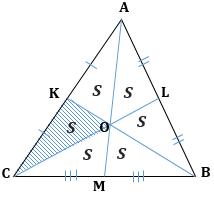
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
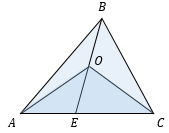
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
2. Через точку `D` проведём прямую `DL«|\|«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«|\|«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«|\|«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
| `S_(m_am_bm_c)=3/4S_(abc)`. |
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
Основные свойства площадей треугольников
Факт 1.
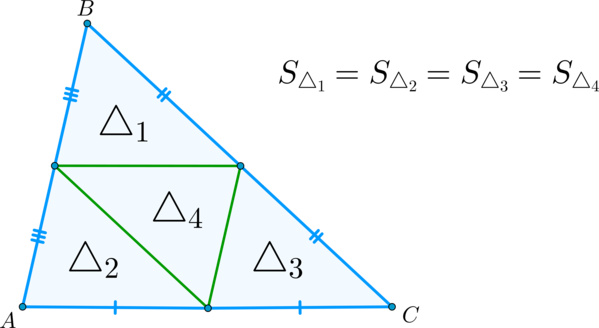
\(\bullet\) Средние линии треугольника разбивают его на 4 равных треугольника.
Соответственно, площади этих треугольников равны.
Факт 2.
\(\bullet\) Медиана треугольника делит его на два треугольника, равных по площади (равновеликих).
Факт 3.
\(\bullet\) Все 3 медианы треугольника делят его на 6 равновеликих треугольников.
Факт 4.
\(\bullet\) Площади треугольников, имеющих одинаковый угол, относятся как произведения сторон, образующих этот угол.
Факт 5.
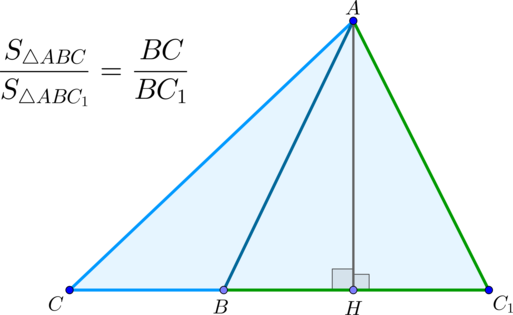
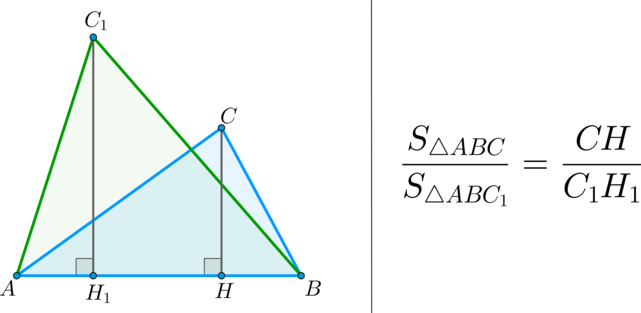
\(\bullet\) Площади треугольников, имеющих одинаковое основание, относятся как высоты, проведенные к этим основаниям.
Факт 6.
\(\bullet\) Площади треугольников, имеющих одинаковую высоту, относятся как основания, к которым проведена эта высота.
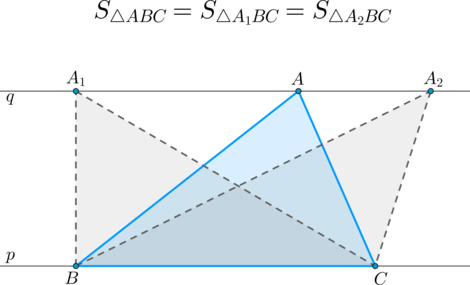
Факт 7.
\(\bullet\) Если прямые \(p\) и \(q\) параллельны, то
Факт 8.
\(\bullet\) Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
\(\bullet\) Отношение периметров подобных треугольников равно коэффициенту подобия.
51. Планиметрия  Читать 0 мин.
Читать 0 мин.
51.506. Отношения
Зачастую в геометрических задачах в условии даются отношения отрезков и площадей или отношение отрезков нужно найти. Существует ряд теорем и свойств фигур и их элементов, в которых так или иначе используются отношения.
ОТНОШЕНИЯ ОТРЕЗКОВ:
1. Все медианы треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 к 1, считая от вершины: AO : AM = 2 : 1.
4. Диагонали параллелограмма точкой пересечения делятся пополам.
Произвольный параллелограмм или ромб:
Прямоугольник или квадрат:
ОТНОШЕНИЯ ПЛОЩАДЕЙ:
2. Треугольник делится тремя медианами на шесть равновеликих треугольников:
ЛЕММЫ О ПЛОЩАДЯХ ТРЕУГОЛЬНИКА:
Площади подобных фигур относятся как квадрат коэффициента подобия.
Если стороны треугольников с общей вершиной лежат на одной прямой, то их площади относятся как основания.
Если два треугольника имеют общую сторону, то их площади соотносятся как длины отрезков BE и OE.
Если два треугольника имеют общий угол, то их площади соотносятся как произведения соответствующих сторон, прилежащих к этому углу.
Лемма 4 применима даже в том случае, если точки нового треугольника были взяты не на сторонах, а на продолжениях сторон. Пусть точка Е лежит на продолжении стороны AB за вершину В.
Метод площадей для решения задач
\(\blacktriangleright\) Теорема 1. Если вершину треугольника перемещать по прямой, параллельной противолежащей стороне, то площадь при этом останется прежней.
\(\blacktriangleright\) Теорема 2. Если два треугольника имеют равные высоты (общую высоту), то их площади относятся как основания, к которым эти высоты проведены.
\(\blacktriangleright\) Теорема 3. Если два треугольника имеют одинаковые стороны (общую сторону), то их площади относятся как высоты, которые к этим сторонам проведены.
\(\blacktriangleright\) Следствие: Медиана треугольника делит его на два треугольника, равных по площади.
\(\blacktriangleright\) Следствие: Все три медианы треугольника делят его на шесть треугольников, равных по площади.
\(\blacktriangleright\) Теорема 4. Если два треугольника имеют по равному углу (общему углу), то их площади относятся как произведения сторон, образующих эти углы.
\(\blacktriangleright\) Следствие: Биссектриса угла треугольника делит его на два треугольника, площади которых относятся как стороны, образующие этот угол.
\(\blacktriangleright\) Теорема 5. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Доказательство: т.к. треугольники подобны, то все стороны одного треугольника в \(k\) раз больше всех сторон другого, а углы между сходственными сторонами равны. Значит, \[\dfrac
\(\blacktriangleright\) Следствие: Все три средние линии треугольника делят его на четыре равных треугольника, и, как следствие, равных по площади.
Задачи на применение методов измерения площадей в ЕГЭ по математике встречаются ежегодно, поэтому при подготовке к прохождению аттестационного испытания учащимся непременно стоит повторить теорию по данной теме. Уметь справляться с такими заданиями обязательно должны выпускники, сдающие как базовый, так и профильный уровень экзамена. Разобравшись с основной теорией и практическими упражнениями на вычисление площадей плоских фигур, старшеклассники смогут решать задачи с любым количеством действий и рассчитывать на получение достойных баллов по итогам сдачи ЕГЭ.
Как подготовиться к экзамену?
Зачастую найти источник, в котором представлен весь базовый теоретический материал, оказывается не так легко, как может показаться на первый взгляд. В нужный момент школьного учебника может просто не быть под рукой. А найти необходимые формулы иногда оказывается достаточно сложно даже в Интернете.
Образовательный портал «Школково» поможет вам подготовиться к сдаче аттестационного испытания. Все основы теории по теме «Измерение площадей плоских фигур» систематизированы и изложены нашими специалистами с учетом их богатого опыта в максимально доступной форме. Ознакомившись с представленной информацией, выпускники смогут восполнить пробелы в знаниях.
Чтобы качественно подготовиться к ЕГЭ, школьникам из Москвы и других городов необходимо не только повторить теорию по теме «Вычисление площадей плоских фигур», но и попрактиковаться в выполнении соответствующих упражнений. Найти задачи вы можете в разделе «Каталог». Для каждого задания наши специалисты прописали подробный алгоритм решения и указали правильный ответ. Последовательно выполняя простые и более сложные упражнения по данной теме, учащиеся смогут отработать навык решения подобных задач. Перечень заданий в соответствующем разделе постоянно дополняется и обновляется.
Ознакомиться с теорией и попрактиковаться в решении задач на вычисление площади треугольника и других фигур, подобных тем, которые включены в ЕГЭ, можно в режиме онлайн. При необходимости любое упражнение можно сохранить в «Избранное». Еще раз повторив базовую теорию, выпускник может в дальнейшем вернуться к задаче на вычисление площади фигуры с целью обсуждения алгоритма ее решения со своим преподавателем.









 Читать 0 мин.
Читать 0 мин.