что такое симметрия в природе
Wonder Wild World
Страницы
Симметрия в природе
«Симметрия – символ красоты, гармонии и совершенства»
Во всем царит гармонии закон, И в мире всё суть ритм, аккорд и тон. Дж. Драйден
Внимательно приглядевшись к природе, можно увидеть общее даже в самых незначительных вещах и деталях, найти проявления симметрии. Форма листа дерева не является случайной: она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок, одна из которых расположена зеркально относительно другой. Симметрия листка упорно повторяется, будь то гусеница, бабочка, жучок и т.п.
Простейший вид симметрии зеркальная (осевая), возникающая при вращении фигуры вокруг оси симметрии.
В природе зеркальная симметрия характерна для растений и животных, которые произрастают или двигаются параллельно поверхности Земли. Например, крылья и туловище бабочки можно назвать эталоном зеркальной симметрии.
 |
| Симметрия, возникающая при вращении фигуры вокруг центра вращения, называется центральной. |
Также существует винтовая симметрия.
Трансляцию можно комбинировать с отражением или поворотом, при этом возникают новые операции симметрии.
Пример винтовой симметрии – расположение листьев на стебле многих растений.
Если рассматривать расположение листьев на ветке дерева мы заметим, что лист отстоит от другого, но и повернут вокруг оси ствола.
Листья располагаются на стволе по винтовой линии, чтобы не заслонять друг от друга солнечный свет. Головка подсолнечника имеет отростки, расположенные по геометрическим спиралям, раскручивающимся от центра наружу. Самые молодые члены спирали находятся в центре. В таких системах можно заметить два семейства спиралей, раскручивающихся в противоположные стороны и пересекающихся под углами, близкими к прямым.
Но какими бы интересными и привлекательными ни были проявления симметрии в мире растений, там еще много тайн, управляющих процессами развития. Вслед за Гете, который говорил о стремлении природы к спирали, можно предположить, что движение это осуществляется по логарифмической спирали, начиная всякий раз с центральной, неподвижной точки и сочетая поступательное движение (растяжение) с поворотом вращения.
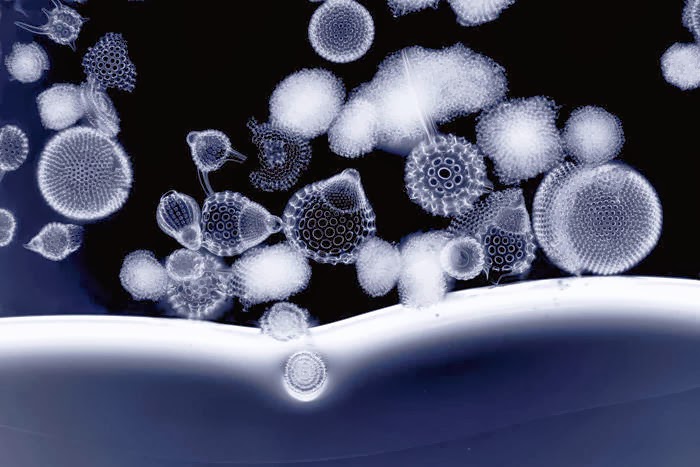
Этому всеобщему закону из двух постулатов подчиняются не только цветы, животные, легкоподвижные жидкости и газы, но и твердые, неподатливые камни. Этот закон влияет на изменчивые формы облаков. В безветренный день они имеют куполовидную форму с более или менее ясно выраженной радиально-лучевой симметрией. Влияние универсального закона симметрии является по сути дела чисто внешним, грубым, налагающим свою печать только на наружную форму природных тел. Внутреннее их строение и детали ускользают из-под его власти.
Что такое симметрия в природе
Симметрия в природе
Автор работы награжден дипломом победителя III степени
Введение
Гуляя осенью в роще, я собрал красивые опавшие листья и принес их домой. Мой папа (Радионов А. А., научный сотрудник Южного математического института ВНЦ РАН), глядя на них, проронил фразу: вот ещё один пример симметрии в природе. Я заинтересовался и первым делом посмотрел в словаре С.И.Ожегова, что означает слово «симметрия», а потом стал приставать к отцу с расспросами: как он определил, что перед нами «симметрия» и каких видов бывает симметрия? Это и послужило поводом изучить этот вопрос.
Цель работы: показать, какие виды симметрии наблюдаются в природе, и как они описываются при помощи математики.
— дать описание различных видов симметрии;
— попытаться самостоятельно найти математические соотношения в строении листьев деревьев.
Объект исследования: кленовые и виноградные листья.
Предмет исследования: симметрия в природных объектах.
Методы, используемые в работе: анализ литературы по теме, научный эксперимент.
Данная работа относится к реферативно-экспериментальной.
Значимость полученных результатов заключается в том, что листья растений могут быть изучены математически, измерены инструментально и симметричность этих природных объектов может быть проверена.
Симметрия в окружающей нас природе
Симметрия (древнегреческое – «соразмерность») – закономерное расположение подобных (одинаковых) частей тела или форм живого организма относительно центра или оси симметрии. При этом подразумевается, что соразмерность – часть гармонии, правильного сочетания частей целого [7].
Гармония – греческое слово, обозначающее «согласованность, соразмерность, единство частей и целого». Внешне гармония может проявляться в симметрии и пропорциональности.
Симметрия очень распространенное явление, ее всеобщность служит эффективным методом познания природы. В живой природе симметрия не абсолютна и всегда содержит некоторую степень асимметрии. Асимметрия – (греческое «без» и «симметрии») – отсутствие симметрии.
Внимательно рассматривая природные явления, можно увидеть общее даже в самых незначительных вещах и деталях, найти проявления симметрии. Форма листа дерева не является случайной: она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок, одна из которых расположена зеркально относительно другой. Симметрия листка повторяется для всех листиков данного дерева. Это пример зеркальной симметрии – когда объект можно разделить на правую и левую или верхнюю и нижнюю половины воображаемой осью, называемой осью зеркальной симметрии. Находящиеся по разные стороны оси половинки почти идентичны друг другу. Зеркало в точности воспроизводит то, что оно «видит», но рассмотренный порядок является обращенным: правая рука у двойника в зеркале оказывается левой. Зеркальную симметрию можно обнаружить повсюду: в листьях и цветах растений. Более того, зеркальная симметрия присуща телам почти всех живых существ (Приложение №1, рис. а).
Поворот на определенное число градусов, сопровождаемый увеличением размера вдоль оси поворота (или уменьшением размера или же без изменения размера), порождает винтовую симметрию – симметрию винтовой лестницы (Приложение №1, рис. в).
Симметрия подобия. Еще один вид симметрии – симметрия подобия, связанная с одновременным увеличением или уменьшением подобных частей фигуры и расстояний между ними. Такую симметрию демонстрируют все растущие организмы: маленький росток любого растения содержит все особенности зрелого растения. Симметрия подобия повсеместно проявляется в природе на всем, что растет: в растущих предметах растений, животных и кристаллов (Приложение №1, рис. г).
В математике самоподобные геометрические объекты называются фракталами [1,4-6]. Для фракталов характерно, что малая часть геометрической кривой подобна всей кривой. На рисунке представлен процесс построения самоподобных кривой Коха и снежинки Коха (первые 4 шага). (приложение №2)
Любой отрезок построенной таким образом кривой имеет бесконечную длину. Фракталы характеризуются фрактальной размерностью. Термин фрактал и фрактальная размерность были введены математиком Бенуа Мандельбротом в 1975 г [6]. Фрактальная размерность была введена как коэффициент, описывающий геометрически сложные формы, для которых детали являются более важными, чем полный рисунок.
Размерность 2 означает, что любую кривую мы можем однозначно определить двумя числами. Поверхность сферы двумерна (ее можно определить с помощью двух углов широты и долготы). Размерность определяется следующим образом: для одномерных объектов – увеличение в два раза их линейного размера приводит к увеличению размеров тоже в два раза. Для двумерных объектов увеличение в два раза линейных размеров приводит к увеличению размера (площадь прямоугольника) в четыре раза. Для 3-х мерных объектов увеличение линейных размеров в два раза приводит к увеличению объема в восемь раз.
Размерность D может быть определена математически с помощью правила:
где N –N число деталей, – коэффициент масштаба, D – размерность.
Отсюда для размерности получим формулу:
Возьмем отрезок, поделим его на три равные части (N = 3), каждая полученная часть будет длиной в 3 раза меньше (), чем длина начального отрезка:
следовательно для отрезка размерность равняется одному.
Аналогично для площади: если измерить площадь квадрата, а затем измерить площадь квадрата со стороной длинною от длины стороны начального квадрата, то она окажется в 9 раз меньше (N = 9) площади начального квадрата:
для плоской фигуры размерность равняется двум. Для пространственной фигуры, такой как куб, вычисленная размерность равняется трем.
Аналогичные вычисления для кривой Коха дают результат:
следовательно фракталам соответствует не целая, а дробная размерность.
Проведение научного эксперимента
В качестве экспериментального материала выбраны опавшие листья деревьев: клена и винограда на внешний вид симметричные (осевая, зеркальная симметрия).
— Измерение площади левой и правой частей листа;
— Измерение углов между прожилками на листе;
— Измерение длин прожилок, имеющихся на листе;
— Запись полученных результатов;
— Поиск математических закономерностей;
— Выводы по полученным результатам.
Список того, что надо изучить на листе дерева:
Рассмотрение опавших листьев показало, что листья симметричны относительно своей оси. Более подробное рассмотрение показывает, что симметрия незначительно нарушается на краях листа, а в некоторых случаях и внутри поверхности листа.
Чтобы убедиться, насколько левая и правая части листа одинаковы, были проведены следующие измерения:
1) измерение площади левой и правой частей листа;
2) измерение углов, под которым пересекаются прожилки в левой и правой частях листа;
3) измерение длины основных прожилок в левой и правой частях листа;
4) измерение длины вторичных прожилок в левой и правой частях листа;
5) измерение длины самых мелких прожилок листа.
На фотографиях показан процесс проведения измерений (Приложение № 3).
Кленовый лист
1) измерение площади левой части показало 317 квадратиков по 25 мм 2 или 79,25 квадратных сантиметров. Измерение правой части показало 312 квадратиков по 25 мм 2 или 78 квадратных сантиметров. С учетом погрешности в точности измерений полученный результат говорит о том, что приблизительно площади левой и правой частей листа одинаковы (Приложение №4, рис. 1).
Виноградный лист
Не менее интересно измерение углов, под которыми пересекаются вторичные прожилки (которые отходят не от центра основания листа). Эти измерения представлены на рисунке 2 Приложения №5: для вторичных прожилок листа наблюдается больший разброс значений углов, под которыми они пересекаются с другими прожилками, но в среднем этот угол составляет приблизительно 60 градусов. Этот средний угол одинаков как в левой части листа, так и в правой его части. Здесь же отмечены длины этих вторичных прожилок.
Для виноградного листа удается измерить и длину сетки самых мелких прожилок. Они отчетливо видны на задней поверхности листа. Измерения длин самых маленьких прожилок проводились при помощи подсчета их количества на половине расстояния между двумя вторичными прожилками, после чего найденное количество умножалось на их длину одной из них (приблизительно половина расстояния между двумя основными прожилками). При этом из подсчета могли выпадать мелкие прожилки, которые не соединяются с основными прожилками и находятся между более крупных прожилок.
Удивительный вывод состоит в том, что чем меньше прожилки, тем больше их общая длина. В левой части листа отношение измеренных длин:
самые мелкие прожилки / вторичные прожилки = 110,7 / 41,2 = 2,69;
вторичные прожилки / основные прожилки = 41,2 / 16,0 = 2,57.
В правой части аналогичные отношения есть
Полученные отношения длин точнее для отношения вторичных к основным прожилкам, поскольку эти длины измеряются более точно. Для левой части отношение длины самых мелких прожилок к длине вторичных прожилок также дает приблизительно такое же значение около 2,7. Только в правой части листа это отношение заметно больше и равно 3,11.
Из измерения длин и углов пересечения прожилок можно сделать следующие выводы.
В левой и правой частях листа наблюдаются приблизительно одинаковые углы между основными и вторичными прожилками.
Также в левой и правой частях приблизительно одинаковы и длины основных и вторичных прожилок.
Найденная закономерность может объясняться фрактальной структурой листа: при переходе от крупного масштаба к более мелкому масштабу наблюдается приблизительно один коэффициент увеличения длины соответствующих прожилок.
Применим формулу фрактальной размерности для листа винограда.
для левой части листа:
количество основных: 2;
длина основных: 16,0 см;
количество вторичных: 12;
длина вторичных 41,2 см;
количество самых мелких прожилок: 407;
длина самых мелких прожилок 110,7 см;
Вычисления фрактальной размерности для геометрического фрактала на этапах 2) и 3) должны дать близкие значения. Полученные цифры различаются более чем в два раза. Это говорит о том, что прожилки виноградного листа не образуют геометрического фрактала. Аналогичный вывод следует из сравнения углов, под которыми пересекаются прожилки разных уровней (40, 60, 90 градусов).
Заключение
Такое поведение прожилок не является фрактальной структурой виноградного листа: измерение фрактальной размерности дает различные значения для прожилок разного уровня. Наблюдающаяся сложная структура прожилок листьев образуется для снабжения водой и питательными веществами всей площади листа растения. По всей видимости, фрактальная структура прожилок листьев не всегда является наилучшей (оптимальной) формой для выполнения этой задачи растением.
Список использованной литературы:
Ссылки на монографии и учебные пособия
1.Пайтген Х.О., Рихтер П.Х., Красота фракталов. Образы комплексных динамических систем//Мир.- М., 1993 г., 206 с. ISBN 5-03-001296-6
2. Тарасов Л.В. Этот удивительно симметричный мир//Просвещение.-М.,1982-с.176
2. Ссылки на статьи из энциклопедий и словарей
3. Ожегов С.И. Словарь русского языка // Русский язык.-20-е изд. М.,1988-с.585
10 превосходных примеров симметрии в природе
На протяжении веков симметрия остается предметом, который очаровывает философов, астрономов, математиков, художников, архитекторов и физиков. Древние греки были совершенно одержимы ею – и даже сегодня мы, как правило, сталкиваемся с симметрией во всем от расположения мебели до стрижки волос.
Просто имейте в виду: как только вы осознаете это, вы, вероятно, испытаете непреодолимое желание искать симметрию во всем, что видите.
Возможно увидев брокколи романеско в магазине, вы подумали, что это ещё один образец генномодифицированного продукта. Но на самом деле это ещё один пример фрактальной симметрии природы. Каждое соцветие брокколи имеет рисунок логарифмической спирали. Романеско внешне похожа на брокколи, а по вкусу и консистенции – на цветную капусту. Она богата каротиноидами, а также витаминами С и К, что делает её не только красивой, но и здоровой пищей.
На протяжении тысяч лет люди удивлялись идеальной гексагональной форме сот и спрашивали себя, как пчелы могут инстинктивно создать форму, которую люди могут воспроизвести только с помощью циркуля и линейки. Как и почему пчелы имеют страстное желание создавать шестиугольники? Математики считают, что это идеальная форма, которая позволяет им хранить максимально возможное количество меда, используя минимальное количество воска. В любом случае, все это продукт природы, и это чертовски впечатляет.
Подсолнухи могут похвастаться радиальной симметрией и интересным типом симметрии, известной как последовательность Фибоначчи. Последовательность Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д. (каждое число определяется суммой двух предыдущих чисел). Если бы мы не спешили и подсчитали количество семян в подсолнухе, то мы бы обнаружили, что количество спиралей растет по принципам последовательности Фибоначчи. В природе есть очень много растений (в том числе и брокколи романеско), лепестки, семена и листья которых отвечают этой последовательности, поэтому так трудно найти клевер с четырьмя листочками.
Но почему подсолнечник и другие растения соблюдают математические правила? Как и шестиугольники в улье, все это – вопрос эффективности.
Помимо растений, некоторые животные, например Наутилус, отвечают последовательности Фибоначчи. Раковина Наутилуса закручивается в «спираль Фибоначчи». Раковина пытается поддерживать одну и ту же пропорциональную форму, что позволяет ей сохранять её на протяжении всей жизни (в отличие от людей, которые меняют пропорции на протяжении жизни). Не все Наутилусы имеют раковину, выстроенную по правилам Фибоначчи, но все они отвечают логарифмической спирали.
Прежде, чем вы позавидуете моллюскам-математикам, вспомните, что они не делают этого специально, просто такая форма наиболее рациональна для них.
Большинство животных имеют двустороннюю симметрию, что означает, что они могут быть разделены на две одинаковых половинки. Даже люди обладают двусторонней симметрией, и некоторые ученые полагают, что симметрия человека является наиболее важным фактором, который влияет на восприятие нашей красоты. Другими словами, если у вас однобокое лицо, то остается надеяться, что это компенсируется другими хорошими качествами.
Некоторые доходят до полной симметрии в стремлении привлечь партнера, например павлин. Дарвин был положительно раздражен этой птицей, и написал в письме, что «Вид перьев в хвосте павлина, всякий раз, когда я смотрю на него, делает меня больным!» Дарвину, хвост казался обременительным и не имеющим эволюционного смысла, так как он не соответствовал его теории «выживания наиболее приспособленных». Он был в ярости, пока не придумал теорию полового отбора, которая утверждает, что животные развивают определенные функции, чтобы увеличить свои шансы на спаривание. Поэтому павлины имеют различные приспособления для привлечения партнерши.
Есть около 5000 типов пауков, и все они создают почти идеальное круговое полотно с радиальными поддерживающими нитями почти на равном расстоянии и спиральной тканью для ловли добычи. Ученые не уверены, почему пауки так любят геометрию, так как испытания показали, что круглое полотно не заманит еду лучше, чем полотно неправильной формы. Ученые предполагают, что радиальная симметрия равномерно распределяет силу удара, когда жертва попадает в сети, в результате чего получается меньше разрывов.
Дайте паре обманщиков доску, косилки и спасительную темноту, и вы увидите, что люди тоже создают симметричные формы. Из-за того, что круги на полях отличаются сложностью дизайна и невероятной симметрией, даже после того, как создатели кругов признались и продемонстрировали свое мастерство, многие люди до сих пор верят, что это сделали космические пришельцы.
По мере усложнения кругов все больше проясняется их искусственное происхождение. Нелогично предполагать, что пришельцы будут делать свои сообщения все более трудными, когда мы не смогли расшифровать даже первые из них.
Независимо от того, как они появились, круги на полях приятно рассматривать, главным образом потому, что их геометрия впечатляет.
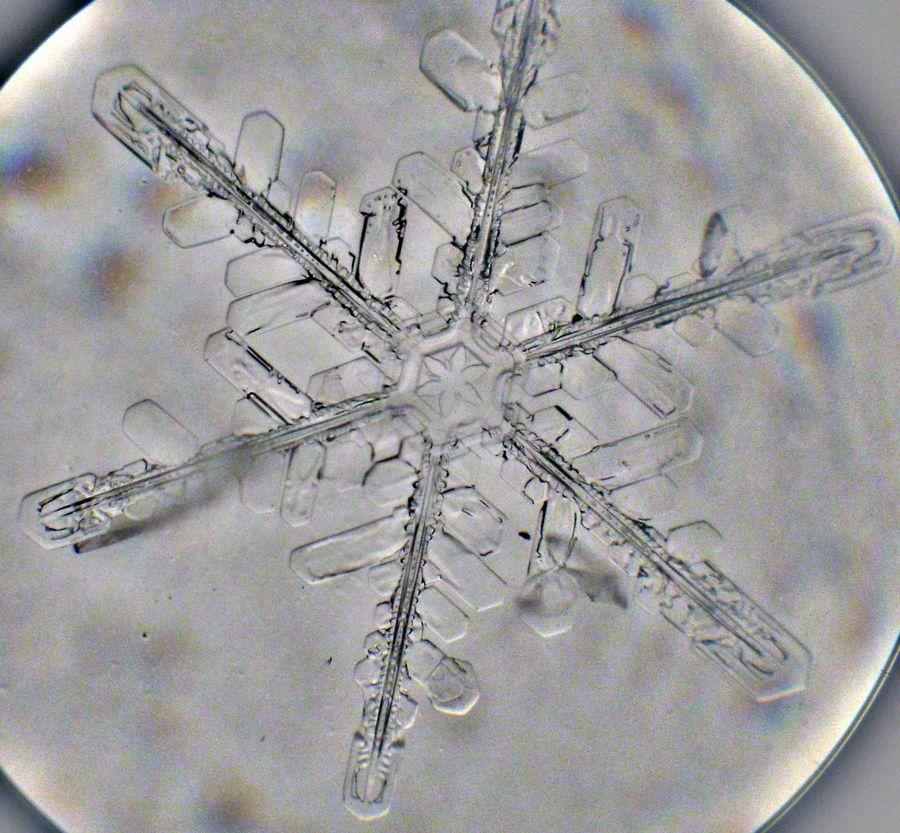
Даже такие крошечные образования, как снежинки, регулируются законами симметрии, так как большинство снежинок имеет шестигранную симметрию. Это происходит в частности из-за того, как молекулы воды выстраиваются, когда затвердевают (кристаллизуются). Молекулы воды приобретают твердое состояние, образуя слабые водородные связи, они выравниваются в упорядоченном расположении, которое уравновешивает силы притяжения и отталкивания, формируя гексагональную форму снежинки. Но при этом каждая снежинка симметрична, но ни одна снежинка не похожа на другую. Это происходит потому, что падая с неба, каждая снежинка испытывает уникальные атмосферные условия, которые заставляют её кристаллы располагаться определенным образом.
Галактика Млечный Путь
Как мы уже видели, симметрия и математические модели существуют почти везде, но разве эти законы природы ограничиваются нашей планетой? Очевидно, нет. Недавно открыли новую секцию на краю Галактики Млечного Пути, и астрономы считают, что галактика представляет собой почти идеальное зеркальное отражение себя.
Если учесть, что Солнце имеет диаметр 1,4 млн. км, а Луна – 3474 км, кажется почти невозможным то, что Луна может блокировать солнечный свет и обеспечивать нам около пяти солнечных затмений каждые два года. Как это получается? Так совпало, что наряду с тем, что ширина Солнца примерно в 400 раз больше, чем Луна, Солнце также в 400 раз дальше. Симметрия обеспечивает то, что Солнце и Луна получаются одного размера, если смотреть с Земли, и поэтому Луна может закрыть Солнце. Конечно, расстояние от Земли до Солнца может увеличиваться, поэтому иногда мы видим кольцевые и неполные затмения. Но каждые один-два года происходит точное выравнивание, и мы становимся свидетелями захватывающих событий, известных как полное солнечное затмение. Астрономы не знают, как часто встречается такая симметрия среди других планет, но они думают, что это довольно редкое явление. Тем не менее, мы не должны предполагать, что мы особенные, так как все это дело случая. Например, каждый год Луна отдаляется примерно на 4 см от Земли, это означает, что миллиарды лет назад каждое солнечное затмение было бы полным затмением. Если и дальше все пойдет так, то полные затмения, в конце концов, исчезнут, и это будет сопровождаться исчезновением кольцевых затмений. Получается, что мы просто находимся в нужном месте в нужное время, чтобы увидеть это явление.
А вы знали, что у нас есть Instagram и Telegram?
Подписывайтесь, если вы ценитель красивых фото и интересных историй!