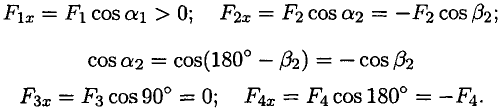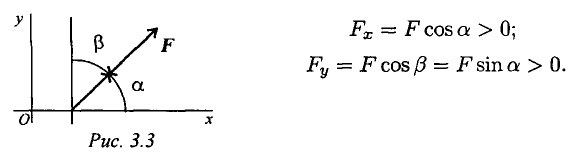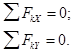что такое проекция силы на ось

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Проекция силы на ось

Часто геометрическое сложение векторов сил требует сложных и громоздких построений. В таких случаях прибегают к другому методу, где геометрическое построе­ние заменено вычислениями скалярных величин. Дости­гается это проектированием заданных сил на оси прямо­угольной системы координат.

Как известнее из математики, осью называют неограни­ченную прямую линию, которой приписано определенное направление. Проекция вектора на ось является скаляр­ной величиной, которая определяется отрезком оси, отсе­каемым перпендикулярами, опущенными из начала и конца вектора на ось.

Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (—), если направление от на­чала проекции к ее концу противоположно положитель­ному направлению оси.

Рассмотрим ряд случаев проектирования сил на ось.

Чтобы найти величину проекции, из начала и конца вектора силы опускаем перпендикуляры на ось х, полу­чаем

Р_х = ab = Р cos α.

Проекция вектора в данном случае положительна.

2. Дана сила Q (рис. б), которая лежит в одной плоскости с осью х, но ее вектор составляет с положи­тельным направлением оси тупой угол α.

Проекция силы Q на ось х

Q_х = ab = Q cos α,

cos a = — cos β.

Так как α > 90°, то cos cos α — отрицательная величина. Выразив cos α через cos β (β — острый угол), оконча­тельно получим

В этом случае проекция силы отрицательна.

Итак, проекция силы на ось координат равна произве­дению модуля силы на косинус угла между вектором силы и положительным направлением оси.

При определении проекции вектора силы на ось поль­зуются обычно косинусом острого угла, независимо от того, с каким направлением оси — положительным или отрицательным — он образо­ван. Знак проекции легче устанавливать непосредствен­но по чертежу.

Силу, расположенную на плоскости хОу, можно спроек­тировать на две координатные оси Ох и Оу. Рассмотрим рисунок.

На нем изображена сила Р и ее проекции Р_х и Р_у. Ввиду того что проекции образуют между собой прямой угол, из прямоугольного треугольника ABC следует:

Этими формулами можно пользоваться для определения величины и направления силы, когда из­вестны ее проекции на координатные оси. Эти же формулы могут применяться для определения величины и направ­ления любого вектора через его проекции.

Источник

Проекция силы на ось

Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора
(рис. 3.1).

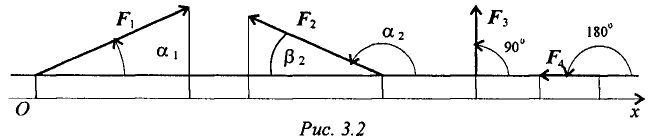
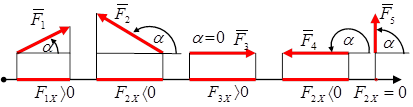
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 3.2).

Проекция силы па две взаимно перпендикулярные оси (рис. 3.3).

Эта теория взята со страницы решения задач по предмету «техническая механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Проекция силы на ось и на плоскость

Проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус – если в отрицательном (рис. 10).

Проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси:

F_X = Fcos .

Проекцией силы на плоскость называется вектор, заключенный между проекциями начала и конца силы на эту плоскость (рис. 11).

F_x = F_xy cos = F cosQcos

F_y = F_xy cos = F cosQcos

Проекция вектора суммы на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось (рис. 12).

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнут – это геометрическое условие равновесия.

Аналитическое условие равновесия.Для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций этих сил на каждую из двух координатных осей были равны нулю.

∑F_ix = 0 ∑F_iy = 0 R =

Теорема о трех силах

Если свободное твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке (рис. 13).

Момент силы относительно центра (точки)

Моментом силы относительно центраназывается величина, равнаявзятому с соответствующим знаком произведению модуля силы на длину h (рис. 14).

Перпендикуляр h, опущенный из центра О на линию действия силы F, называется плечом силы F относительно центра О.

Момент имеет знак плюс, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки, и знак минус – если по ходу часовой стрелки.

Свойства момента силы.

1. Момент силы не изменится при переносе точки приложения силы вдоль ее линии действия.

2. Момент силы относительно центра равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр (плечо равно нулю).

Пара сил. Момент пары.

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рис. 15).

Наикратчайшее расстояние (перпендикуляр) между линиями действия сил называется плечом пары α.

Действие пары сил на тело сводится к вращательному эффекту, который зависит:

1) от модуля F сил пары и длины ее плеча α;

2) положения плоскости действия пары;

3) направления поворота в этой плоскости.

Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо:

Момент пары будет считаться положительным, если пара стремится повернуть тело против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.

Алгебраическая сумма моментов пары сил относительно любого центра, лежащего в плоскости ее действия, не зависит от выбора этого центра и равна моменту пары:

Теорема об эквивалентности пар. Не изменяя оказываемого на тело действия, можно пару сил, приложенную к абсолютно твердому телу, заменить любой другой парой, лежащей в той же плоскости и имеющей тот же момент. Из этой теоремы вытекают следующие свойства пары сил:

1) данную пару, не изменяя оказываемого ею на тело действия, можно перенести куда угодно в плоскости действия пары;

2) у данной пары, не изменяя оказываемого ею на тело действия, можно произвольно менять модуль силы или длину плеча, сохраняя неизменным ее момент.

Теорема. Действие пары сил на твердое тело не изменится, если пару сил перенести из данной плоскости в любую другую плоскость, ей параллельную.

Сложение пар, лежащих в одной плоскости

Теорема о сложении пар. Система пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых пар:

Для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма этих пар была равна нулю:

Данное равенство является условием равновесия пар.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Реакция связи приложена к телу или к связи?

2. Перечислите основные типы связей

3. Сколько компонент реакции имеет каждый тип связей и куда они направлены?

4 Сформулируйте понятие «алгебраический момент силы».

5. Что значит «плечо силы»?

6. Как определяется знак алгебраического момента силы?

7. Что такое «пара сил»?

8 Что значит «плечо пары»?

9. Как определяется алгебраический момент пары и его знак?

Источник

Проекция силы на ось.

Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси:

F_X 2 + R_у 2 ) 1/2 = 0, что возможно, если одновременно R_х = 0, R_у = 0. Следовательно, для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на оси координат Оху были равны нулю, то есть:

1.4.2 Теорема о трех непараллельных силах.

Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действияэтих силпересекаются в одной точке.

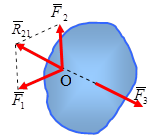
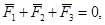
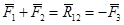
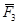
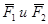
Так как, то . Следовательно, согласно аксиоме 1, (см. п. 1.1.2) линия действия силы пересекает точку О сходимости сил .

Дата добавления: 2016-01-29 ; просмотров: 3285 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Техническая механика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

4. Определение равнодействующей аналитическим способом

Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.

Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.

Проекция силы на две взаимно перпендикулярные оси.

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.

Модуль (величину) равнодействующей можно определить по известным проекциям:

Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:

Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской системы сходящихся сил:

При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

Источник