В чем преимущество двоичной системы счисления экономия памяти компьютера

Замена двоичной логики — увеличит ли это производительность?

Наверняка на хабре уже немало постов на эту тему. Тем не менее, я попытаюсь рассказать свою точку зрения на всё это…

Однажды я прочитал в интернете про троичную систему счисления и заинтересовался. Меня мучил вопрос, а нельзя использовать в основе компьютера симметричную троичную систему счисления (СС), и даже вдруг это увеличит производительность компьютера? Мне казалось, что это возможно, и я жаждал это проверить.

Информация:
Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3. Существует в двух вариантах: несимметричная и симметричная.
В несимметричной троичной системе счисления чаще применяются цифры <0,1,2>, а в симметричной троичной системе счисления знаки <−,0,+>, <−1,0,+1>.
У некоторых людей эта логика вызывает затруднения. Они говорят, например, приведите пример подобной логики в жизни.
Человек, немного подумавший над этой логикой поймет, что она более жизненна чем двоичная. Обычный пример троичной логики в жизни связан с постоянным током: ток движется в одну сторону, в другую сторону, его нет.

Оказалось, что симметричная троичная система счисления использовалась давным-давно для решения «задачи о гирях», использовалась в компьютере Сетунь, построенном в 50-е годы в МГУ. С 2008 года в университете « California Polytechnic State University of San Luis Obispo» функционирует цифровая компьютерная система TCA2, основанная на троичной системе счисления.

В чем же плюсы троичной СС над двоичной? Рассмотрим эти плюсы:

Меньше разрядов

Емкость

Экономичность системы счисления

Экономичность системы счисления — запас чисел, который можно записать в данной системе с помощью определенного количества знаков. Чем больше запас тем экономичнее система. По затратам числа знаков (в трёхразрядном десятичном числе 3*10=30 знаков) наиболее экономична из позиционных показательных несимметричных систем счисления. Обозначим p основание системы счисления, n количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел которое при этом можно записать будет равно pn/p.

Мы рассмотрели троичную арифметику, теперь затронем логику:

В чем же проблемы двоичной логики?
1.Мощности компьютера, основанного на двоичной логике, не всегда хватает. Приведем пример. Одна из наиболее сложных систем защиты – криптосистема RSA. Вскрытие шифра RSA с длиной ключа 1024 бита (такая длина часто используется в информационных системах) займет в лучшем случае — при проведении распределенных вычислений на тысячах мощных ПК — не менее пятнадцати лет, а к тому времени данная система шифровки перестанет быть востребованной.
Докажем математически какая система счисления будет наилучшей для максимальной мощности и емкости памяти. Для этого рассмотрим функцию f(p)=p^(n/p), в которой p – основание системы счисления, а n – количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел, которое при этом можно записать, будет равно pn/p

f(p)=p^(n/p)
Для того, чтобы определить максимальное значение функции, найдем ее производную:
ln f = ln p^(n/p)
ln f =n/p* ln p
. (Я не буду приводить здесь всю математику)
n*p^(n/p-2) никогда не будет равно 0 => (1 — ln⁡ p)=0, ln p = 1, p = e
e = 2,71, а ближайшее целое число к нему – это три.
Значит, в этом плане лучшая система с целочисленным основанием — троичная.

Самое вкусненькое — рассмотрим троичные логические операции:

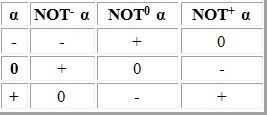
1.Отрицание

2.Конъюнкция — логическое И

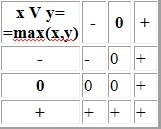
3.Дизъюнкция — логическое ИЛИ

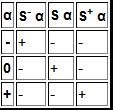
4.Операция Выбора. Эта операция существует только для троичной логики. Таблица истинности каждой из этих трёх операций содержит везде „-“, кроме единственного значения, которое ею можно выбрать.

5.Модификация. Полное название этих одноместных операций: увеличение на единицу по модулю три (INC) и уменьшение на единицу по модулю три (DEC). Увеличение на единицу по модулю три – это циклическое прибавление единицы.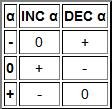

Здесь видны и прежде знакомые вам логические операции из двоичной логики, но добавились и новые…

Квантовые компьютеры

Квантовый компьютер — вычислительное устройство, работающее на основе квантовой механики. Квантовый компьютер принципиально отличается от классических компьютеров, работающих на основе классической механики.
Благодаря огромной скорости разложения на простые множители, квантовый компьютер позволит расшифровывать сообщения, зашифрованные при помощи популярного асимметричного криптографического алгоритма RSA. До сих пор этот алгоритм считается сравнительно надёжным, так как эффективный способ разложения чисел на простые множители для классического компьютера в настоящее время неизвестен. Для того, например, чтобы получить доступ к кредитной карте, нужно разложить на два простых множителя число длиной в сотни цифр. Даже для самых быстрых современных компьютеров выполнение этой задачи заняло бы больше времени, чем возраст Вселенной, в сотни раз. Благодаря алгоритму Шора эта задача становится вполне осуществимой, если квантовый компьютер будет построен.
Канадская компания D-Wave заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит. Это устройство работает на кубитах — квантовых аналогах битов.
Но можно построить компьютеры не на битах, а на кутритах — аналогах трита в квантовом компьютере.
Кутрит (квантовый трит) — квантовая ячейка, имеющая три возможных состояния.
Подлинное новаторство метода Ланьона в том, что, используя в универсальных квантовых вентилях кутриты вместо кубитов, исследователи могут существенно снизить количество необходимых вентилей.
Ланьон утверждает, что компьютер, который в обычном случае использовал бы 50 традиционных квантовых вентилей, сможет обойтись всего девятью, если будет основан на троичном представлении.
Также, согласно некоторым исследованиям, использование кутритов вместо кубитов позволит упростить реализацию квантовых алгоритмов и компьютеров.

Итог:
В конечном итоге видно, что троичная симметричная система лучше двоичной системы в некоторых показателях, но не сильно выигрывает. Но с пришествием квантовых компьютеров троичные вычисления получили новую жизнь. Универсальные квантовые логические вентили — краеугольный камень новорожденных квантовых вычислительных систем — требует сотни вентилей для завершения одной полезной операции. Квантовый компьютер канадской компании D-Wave, анонсированный в прошлом году, состоит всего из 16 квантовых битов — кубитов — минимум, необходимый для управляемого вентиля «NOT». Использование в квантовом компьютере кутритов нужно было бы намного меньше вентилей для завершения одной операции. Я думаю, если бы началось производство и тестирование таких компьютеров, то результаты были бы лучше, чем у обычных компьютеров, вскоре началось бы массовое их производство, и про двоичные компьютеры все бы забыли…

Источник

Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной?

Обсуждение вопроса:

Достоинства двоичной системы счисления заключаются в простоте реализации процессов хранения, передачи и обработки информации на компьютере. Для ее реализации нужны элементы с двумя возможными состояниями, а не с десятью. Представление информации посредством только двух состояний надежно и помехоустойчиво. Возможность применения алгебры логики для выполнения логических преобразований. Двоичная арифметика проще десятичной.

Недостатки двоичной системы счисления. Код числа, записанного в двоичной системе счисления представляет собой последовательность из 0 и 1. Большие числа занимают достаточно большое число разрядов. Такая запись громоздка и в ней неудобно производить операции. Быстрый рост числа разрядов — самый существенный недостаток двоичной системы счисления.

Этот недостаток немного компенсируется тем, что в двоичной системе правила арифметики очень просты, а таблицы сложения и умножения содержат всего по четыре элемента.

Преимущества двоичной системы счисления:

• Простота совершаемых операций.

• Возможность осуществлять автоматическую обработку информации, реализуя только два состояния элементов компьютера.

Недостаток двоичной системы счисления:

• Быстрый рост числа разрядов в записи, представляющей двоичное число.

Источник

В чем преимущество двоичной системы счисления?

1. Экономия памяти компьютера; 2. Электрические элементы с такой конструкцией потребляют гораздо меньше энергии; 3. Транзисторы, чье состояние, прежде всего, характеризуется двумя состояниями, легче всего воспроизводимы; 4. Двоичный код не подвержен ошибкам.

13. Для просмотра Web- страниц предназначены…

1. поисковые серверы 2. программы браузеры 3. телеконференции

4. почтовые программы 5. провайдеры

14. Сколько символов текста можно передать за 5 секунд, используя модем, работающий со скоростью 14400 бод (1 бод = 1 бит/с)?

1. 1800 2. 900 3. 180 4. 72000 5. 9000

15. Дано исходное состояние таблицы.

После выполнения команды КОПИРОВАТЬ А5: В5 в А4 : В1 значения клеток А6 и В6 будут равны соответственно:

1. будет выдано сообщение об ошибке – ошибка в формуле;

2. 0,25 и 0,5 3. 64 и 128

16. Из данных адресов (1) MERY@@VERY.ru (2) zxcvb@qwerty.asd (3) qlavk.msu@ адресами электронной почты могут быть только:

1. (1) 2. (2) 3. (3) 4. (1) и (2) 5. (1) и (3)

17. Устройство необходимое для обмена информацией с другими компьютерами по телефонным каналам – это:

1. сканер; 2. модем; 3. дисковод; 4. плоттер; 5. стример

Какие значения будут находиться в ячейках С2, С3, С4 после выполнения расчётов по заданным формулам?

1. С2=324; С3=12; С4=168; 2. С2=26; С3=18; С4=22; 3. С2=26; С3=12; С4=19;

4. С2=26; С3=12; С4=21,333;

5. С2=324; С3=12; С4=21,333

Что не является средством телекоммуникации?

1. телефон 2. телевизор 3. радио 4. печатная машинка 5. факс

20. Дан адрес электронной почты den@duble.immc.ru. Каково имя почтового сервера?

1. den; 2. immc; 3. duble; 4. duble.immc; 5. ru

21. Дисковод магнитного диска – это устройство для…

1. только для записи информации; 2. хранения информации; 3. обработка информации;

4. только для чтения информации; 5. чтения и записи информации

22. Браузеры (например, Internet Explorer) являются…

1. сервисами Internet 2. почтовыми программами 3. средством создания Web- страниц

4. средством просмотра Web- страниц 5. средством ускорения работы коммуникационной сети

23. Совокупность правил, определяющих процедуру взаимодействия в сети, называется …

1. механизмом коммутации; 2. топологией; 3. протоколом; 4. этикетом; 5. доменом.

24. Для быстрого получения гипертекстового документа необходимо указать в адресной строке браузера его…

1. HTML – адрес 2. IP-адрес 3. TCP/IP-адрес 4. TCP-адрес 5. URL-адрес

Источник

В чем преимущество двоичной системы счисления?

1. Экономия памяти компьютера; 2. Электрические элементы с такой конструкцией потребляют гораздо меньше энергии; 3. Транзисторы, чье состояние, прежде всего, характеризуется двумя состояниями, легче всего воспроизводимы; 4. Двоичный код не подвержен ошибкам.

Какое минимальное число можно записать в двоичной системе счисления 6 цифрами?

21. Дано исходное состояние таблицы.

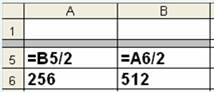
После выполнения команды КОПИРОВАТЬ А5: В5 в А4 : В1 значения клеток А6 и В6 будут равны соответственно:

1. будет выдано сообщение об ошибке – ошибка в формуле;

2. 0,25 и 0,5 3. 64 и 128

Какие значения будут находиться в ячейках С2, С3, С4 после выполнения расчётов по заданным формулам?

1. С2=324; С3=12; С4=168; 2. С2=26; С3=18; С4=22; 3. С2=26; С3=12; С4=19;

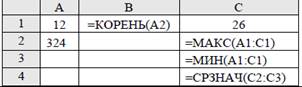
4. С2=26; С3=12; С4=21,333;

5. С2=324; С3=12; С4=21,333

Учащиеся проходят тестирование. Если сумма баллов больше 16, но меньше 19, то ученик получает оценку 4. Выбрать условие, проверяющее получит ли тестируемый оценку 4. Сумма балов хранится в клетке с адресом С10.

1.ИЛИ (С10>16;C10 16;C10 19);

4. И(C10 19); 5. ИЛИ(C10=15;C10=19).

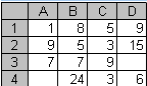
Дан фрагмент электронной таблицы. Определить, какое из утверждений истинно для этого фрагмента таблицы?

1. В ячейку D4 введена формула =(А1+В2+С3)/3; 2. В ячейку D1 введена формула =МАКС(A1:C1); 3.В ячейку В4 введена формула =СУММ(B1:B3)*5; 4.В ячейку С4 введена формула =МИН(A2;A3;C2) 5. В ячейку D2 введена формула =СУММ(A2:C2).

Окно текстового редактора содержит 25 строк по 60 символов в строке. Размер окна графического редактора, работающего в 8-цветном режиме, 80 x 25 пикселей. Страница текста, занимающая весь экран текстового редактора, предается за 10 сек. по каналу электронной почты. Картинка, занимающая все рабочее поле графического редактора, передается за 5 сек. Определить скоростные характеристики модемов, используемых для пересылки текста и графической информации.

1. 1200 бод и 1200 бод; 2. 1200 бод и 2400 бод; 3. 2400 бод и 1200 бод

4. 1200 бод и 3200 бод; 5. 7200 бит/мин и 2400 бод

Диагностическая работа

По ИНФОРМАТИКЕ в 8 классе.

Источник

Проект на тему: «Применение двоичной системы счисления в современности.»

Муниципальное общеобразовательное бюджетное учреждение

«Средняя общеобразовательная школа № 90»

«Применение двоичной системы счисления в современности.»

Выполнил: ученик 8а класса

Глава I что, понимается под словом «число»?

Глава II Позиционные системы счисления

Двоичная система счисления

Системы счисления и их практическое применение

Арифметические операции позиционных СС

Опрос учеников «Умеешь выполнять арифметические операции в двоичной, восьмеричной, шестнадцатеричных СС

В журнале «Юный ученый» Прочитал. высказывание Пьер-Симона Лаплас (1749–1827): Мысль выражать все числа немногими знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна, Десятичная система счисления, которой мы пользуемся, кажется нам единственно удобной и пригодной для вычислений. Но так ли это? Эту проблему я решил выяснить. Задал себе вопрос, какие системы счисления существуют, и какое применение находят различные системы счисления в практической деятельности человека.

Тема « Применение двоичной системы счисления в современности »

Объект исследования: Двоичная система счисления.

Предмет исследования: Применение двоичной системы счисления

Проблема исследования: проблема применения арифметических операций систем счисления у подростков и найти ответ на вопрос «Является ли проблемой арифметические операции в позиционных систем счисления?»

Гипотеза: можно предположить, что Интернет-зависимость проявляется в том, что люди утрачивают способность контролировать свое время в сети, предпочитая виртуальную жизнь реальной .

Узнать о позиционных системах счисления;

Узнать правила перевода позиционных системе счисления;

Провести социальный опрос учащихся «Знаешь в какой профессии используют двоичную систему»

предложить решение этой проблемы.

Анализ учебной литературы;

Методы практического исследования;

Поставил цель исследования. узнать, для чего нужна двоичная система счисления.

Для достижения поставленной цели сформулировали следующие

изучить литературу о позиционных системах счисления,

выяснить вопрос почему в ЭВМ информация представляется в двоичной системе счисления и чем она удобна,

Где еще применяется позиционные системы счисления.

Глава I что понимается под словом «число»?

В книге Иосиф Лазарев «Духовная нумерология. Язык чисел», прочитал. Язык чисел – самый древний из всех существующих языков. Мало того, числа древнее самого мира! Чтобы Бог мог создавать наш мир в первый день, второй, третий и т. д., сначала должны были появиться числа. Существует множество пособий по изучению разных языков. Но пособия по изучению языка чисел до сих пор не существовало. Ведь невозможно считать ныне известные нумерологические изыски учебниками по изучению языка чисел. Сплошь и рядом какие-то надуманные методы, расчёты, многосложная терминология, от которой Ум либо окончательно теряет способность отличать главное от второстепенного, либо вообще приходит в отчаянье, словно студент, заваливший очередной экзамен. Все будто забыли о том, что нумерология – это наука о смысле чисел, а не «трудная игра в цифры». Действительно забыли или никогда не знали? Так или иначе, данная книга представляет собой пособие именно по изучению языка чисел.

Глава II Позиционные системы счисления
2.1 В журнале «Международный школьный научный вестник.» прочитал Система счисления – это способ представления чисел и соответствующие ему правила действий над числами. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Двоичная система счисления

Главный редактор журнала «Международный школьный научный вестник.» кандидат медицинских наук Струкова Наталия Юрьевна журнала объяснила в статье по системам счисления пояснила : Примером позиционной системы счисления может служить система, в среде которой выполняются все операции по всему миру. Возникновение десятичной системы – это одно из самых важных событий в математике. Неудивительно, что история десятичной системы счисления занимает умы многих ученых. Существует несколько версий возникновения системы. Существует версия, что она зародилась в Китае. Есть также предположение, что ее изобрел Аль-Хорезми (узбекский математик). Но более распространенная версия состоит в том, что история возникновения десятичной системы началась в Индии. Сначала в этой системе счисления было всего девять цифр, ноль появился гораздо позднее.

Основоположником двоичной системы является немецкий философ Лейбниц Готфрид Вильгельм. Двоичная система проста, так как для представления информации в ней используются всего два состояния или две цифры. Такое представление информации принято называть двоичным кодированием. Представление информации в двоичной системе использовалось человеком с давних времен. Так, жители островов Полинезии передавали необходимую информацию при помощи барабанов: чередование звонких и глухих ударов (на подобии азбуки Морзе). С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц: 0 – отсутствие электрического сигнала, 1 – наличие электрического сигнала. Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

— для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток и нет тока, намагничен и не намагничен и т.п.), а не, например, с десятью, как в десятичной;

— представление информации посредством только двух состояний надежно и помехоустойчиво;

— двоичная арифметика намного проще десятичной.

Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи. Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Для программистов удобнее работать с более компактной записью.

В итоге было решено использовать альтернативные и более простые системы счисления: восьмеричную и шестнадцатеричную. Числа 8 и 16 являются степенями двойки (2 в третьей и 2 в четвёртой степени соответственно), поэтому выполнять преобразования из двоичной системы и, наоборот, гораздо легче, чем при десятичной системе счисления, которая не может похвастаться своей причастностью к степеням числа 2.

Системы счисления и их практическое применение

Развитие чисел тесно связано с потребностями общества в измерениях, контроле, особенно в областях аграрной, промышленной и налогообложения. Первые области применения чисел были связаны с созерцанием звезд и земледелием. Изучение звездного неба позволило проложить торговые морские пути, караванные дороги в новые районы и резко увеличить эффект торговли между государствами. Обмен товарами приводил к обмену культурными ценностями, к развитию толерантности как явления, лежащего в основе мирного сосуществования различных рас и народов. Понятие числа всегда сопровождалось и нечисловыми понятиями. Например, один, два, много. Эти нечисловые понятия всегда ограждали числа. Числа придавали законченный вид всем наукам, где они применялись.

Для решения математических и физических задач, в которых трудно обойтись только целыми числами, используется представление чисел в форме с плавающей запятой.

В современных компьютерах, в зависимости от типа операционной системы и конкретных прикладных программ, используются 8-разрядные и 16-разрядные (Windows 95, 98, ХР) коды символов. Использование 8-разрядных кодов позволяет закодировать 256 различных знаков, этого вполне достаточно для представления многих символов, используемых на практике. При такой кодировке для кода символа достаточно выделить в памяти один байт. Так и делают: каждый символ представляют своим кодом, который записывают в один байт памяти. В персональных компьютерах обычно используется система кодировки ASCII (American standard Соде for Information Interchange) — американский стандартный код для обмена информации. В этой системе не предусмотрены коды для русского алфавита, поэтому в нашей стране используются варианты этой системы кодировки, в которые включают буквы русского алфавита. Чаще всего используется вариант, известный под названием «Альтернативная кодировка».

Компьютерные технологии постоянно совершенствуются, и в настоящее время все большее число программ начинает поддерживать шестнадцати битовый стандарт Unicode, который позволяет кодировать практически все языки и диалекты жителей Земли в силу того, что кодировка включает в себя 65 536 различных двоичных кодов.

Кроме того, числа в восьмеричной системе как минимум более приятны глазу и гораздо короче, чем их аналоги в двоичной системе.

Учитывая, что спокойно сосуществуют разные системы счисления, вполне логично предположить, что между ними есть связь. Перевести число из одной системы счисления в другую довольно просто. Чтобы перевести из привычной нам десятичной системы в другую надо всего лишь использовать известное нам с начальной школы деление «уголочком» или столбиком. А так как из десятичной переводят делением, то обратно, что вполне логично, переводят умножением.

Арифметические операции позиционных СС

Таблицы сложения в любой позиционной системе счисления легко составить, используя правило счета:

Если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд.

Таблица сложения в двоичной системе :

Таблица сложения в восьмеричной системе:

1) Сложим числа 15 и 6 в различных системах счисления.

Решение. Переведем числа 15 и 6 в двоичную и восьмеричную системы счисления и выполним сложение, используя таблицы сложения (см. выше).

Ответ: 15 + 6 = 2110 = 101012 = 258

Решение: переведем число 5616 в восьмеричную систему счисления, используя поразрядный способ перевода разложением на тэтрады и триады:

Пользуясь правилами сложения в восьмеричной системе счисления, получаем:

Вычитание осуществляется по тем же правилам, что и в десятичной системе счисления.

При вычитании из меньшего числа большего производится заем из старшего разряда.

Вычислим разность X − Y двоичных чисел, если X = 10101002 и Y = 10000102 . Результат представим в двоичном виде.

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Таблица умножения в двоичной системе:

Таблица умножения в восьмеричной системе: A

Умножение многоразрядных чисел в различных позиционных системах счисления происходит по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.

Ответ: 15 ⋅ 12 = 18010 = 101101002 = 2648

Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. Следует только грамотно пользоваться теми цифрами, которые входят в алфавит используемой системы счисления.

При выполнении любых арифметических операций над числами, представленными в разных системах счисления, следует предварительно перевести их в одну и ту же систему.

Опрос учеников «Умеешь выполнять арифметические операции в двоичной, восьмеричной, шестнадцатеричных СС

(СМ. ПРИЛОЖЕНИЕ РИС.1)

Работая над этим проектом, я столкнулись с огромным количеством интересной информации. Я бы хотел бы закончить мое выступление словами немецкого философа Готфрида Вильгельма Лейбница: «Кто хочет ограничиться настоящим, без знания прошлого, тот никогда его не поймет…»

Анкета соц.опроса. (было опрошено 30 человек)

1. Умеешь выполнять арифметические операции в двоичной СС

2. Умеешь выполнять арифметические операции в восьмеричной СС?

3. Умеешь выполнять арифметические операции в шестнадцатеричной СС?

5. 1111111 ₂ сколько это будет в 10 ₁₀

Источник