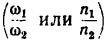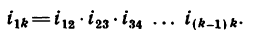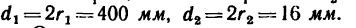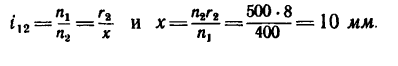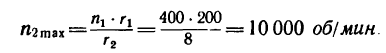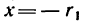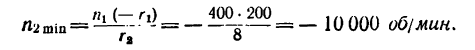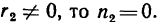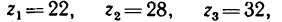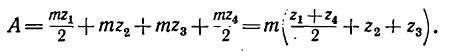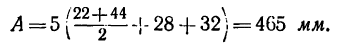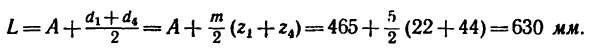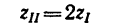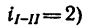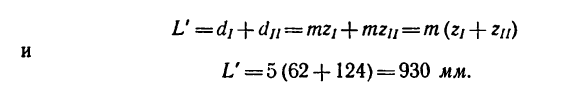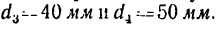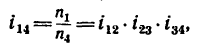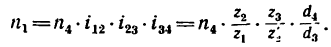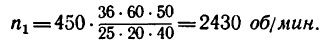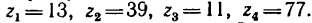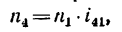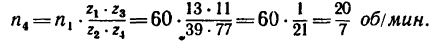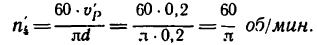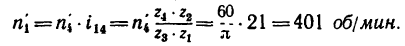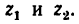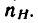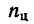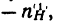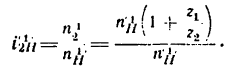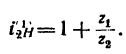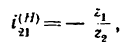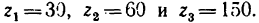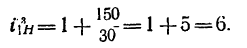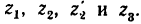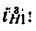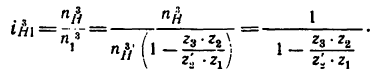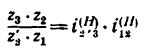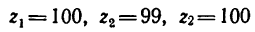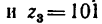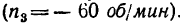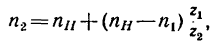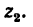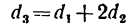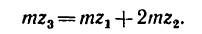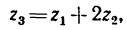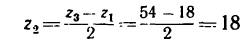передаточное отношение выражается формулой

Передаточное отношение

Одной из важнейших кинематических характеристик в теории механизмов и машин является передаточное отношение. Оно позволяет определить, на какую величину возрастает момент приложенной силы, когда происходит передача вращения от одной детали к другой. На практике для решения различных технических задач механизмы создаются с кинематической схемой, имеющей постоянное или переменное передаточное отношение.

Общее определение

Значение передаточного отношения у кинематических схем рассчитывается по стандартному математическому выражению. Результат получается при проведении математической операции деления значения угловой скорости ведущего вала или шестерёнки, на такой же параметр ведомого вала. Вместо этих значений используют отношение их частот вращения.

Современные кинематические схемы реализованы с использованием следующих механических соединений:

Передача вращения основана на двух физических принципах: с помощью силы трения, с использованием механизмов зацепления. В зависимости от решаемой задачи механизмы изготавливаются с замедлением и ускорением. Первые называются редукторами, вторые — мультипликаторами. Обе разновидности бывают одноступенчатыми, двухступенчатыми, многоступенчатыми.

Пространственное расположение осей определяет следующие виды механизмов:

Все типы механизмов бывают замедляющие и ускоряющие движение. Наиболее частое применение замедляющих конструкций объясняется более высокой скоростью используемых двигателей и необходимостью увеличить мощность выходного элемента кинематической схемы.

В зависимости от соотношения скоростей возникает вопрос: может ли передаточное отношение быть отрицательным? Этот коэффициент является отношением величин имеющих только положительные значения. Он не может быть отрицательным. В зависимости от отношения числителя к знаменателю результат получиться больше единицы или меньше. В первом случает, он справедлив для редукторов, во втором для мультипликаторов.

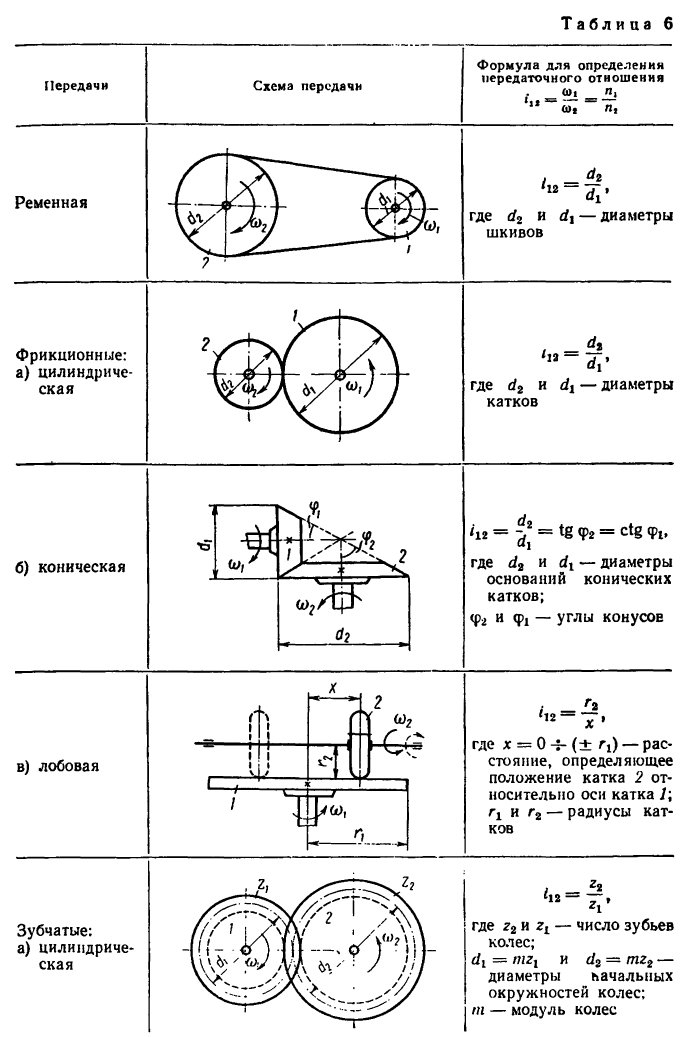
Таблица передаточных отношений является сводным документом. В ней приведены значения основных технических характеристик всех типов кинематических соединений.

В сводной таблице можно найти зависимость значения передаточного числа от допустимой мощности, которая передаётся конкретным видом соединения.

Зубчатая передача

Это механическое соединение двух или более вращающихся валов при помощи специальных колёс, на поверхности которых выточены зубья. Такой тип подразделяется по следующим характеристикам:

Важную роль в понимании работы всего механизма играет передаточное отношение зубчатой передачи. Его вычисляют, используя классическое выражение. Оно находится с подстановкой различных параметров. Например, подсчитывая численность изготовленных зубьев на ведущем и ведомом колесе. Формула позволяет получать результаты с высокой степенью точности:

Где i₁₂ — передаточное отношение от звена 1 к звену 2 (звено 1 — ведущее, звено 2 — ведомое; d₁,d₂ — диаметры звеньев; z₁, z₂ — количество зубьев звеньев (если таковые имеются); M1, M2 — крутящие моменты звеньев; ω₁, ω₂ — угловые скорости звеньев; n₁, n₂ — частоты вращения звеньев.

В большей степени он зависит от количества зубьев расположенных на шестерёнке. Существенным достоинством зубчатого соединения является постоянство расчётного и реального передаточного отношения. Она связано с отсутствием эффекта проскальзывания.

Существенное влияние на величину этого показателя оказывает применяемое количество шестерней и число зубчатых колёс.

Для цилиндрической передачи этот параметр кроме приведенных выше параметров зависит от межосевого расстояния. Цилиндрические зубчатые передачи распространены в различных агрегатах легковых и грузовых автомобилей, тракторов, сельскохозяйственной техники. Их активно используют в трансмиссии.

Зубчатая передача обладает самым большим коэффициентом передачи мощности. Она способна отдавать мощность до 4500 кВт с передаточным числом достигающим 6,3.

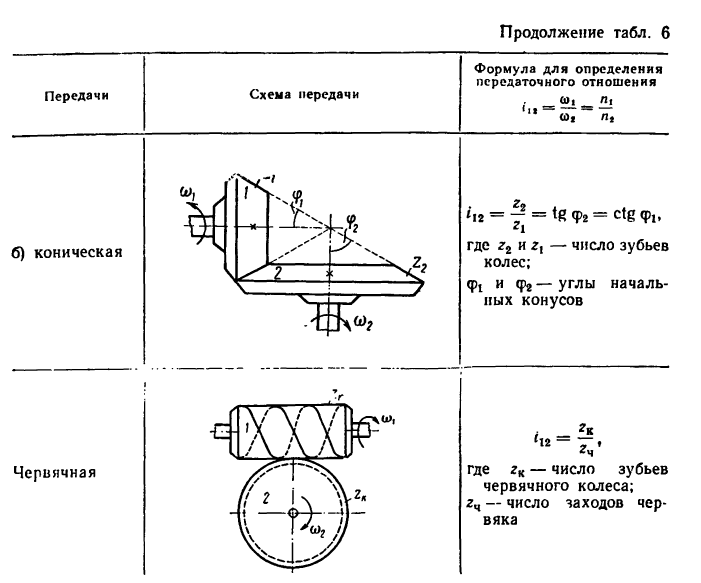
Распространение получили зубчатые конструкции конического типа. Они обладают ортогональным сочленением. Расчёт конической передачи предполагает учёт таких параметров как: делительные диаметры, углы конусов, количество зубьев.

Для получения поступательного движения применяется реечное соединение. Конструктивно она состоит из шестерёнки, рейки с нанесёнными зубьями. Для реечной передачи учитывают диаметр окружности и количество зубьев на колесе, число зубьев расположенных на рейке.

Планетарная передача

Широко применяется так называемая планетарная кинематическая схема. Она представляет собой механизм, предназначенный для передачи, преобразования вращательного движения. С этой целью используются зубчатые колеса, расположенные на перемещающейся оси. Конструктивными элементами являются: центральные зубчатые колеса, закреплённые на неподвижных осях, боковые зубчатые колеса (расположены на перемещающихся осях). Для обеспечения наилучшего эффекта планетарные механизмы изготовляются на параллельных осях.

Максимальное значение передаточного числа достигает 9 единиц.

Коэффициент полезного действия достаточно высокий. Его значение приближается к 0,98. Наиболее распространёнными являются конструкции, в которых применяются нескольких сателлитов. Их располагают с угловыми шагами равной величины.

Такие конструкции выполняются с постоянным или переменным передаточным отношением. Некоторые из них имеют возможность регулировки этого параметра. Они разработаны обратимыми и необратимыми. В обратимых образцах предусмотрено движение в прямом и обратном направлении. В необратимых конструкциях такое движение невозможно. Изменение передаточного отношения бывает ступенчатым или бесступенчатым. Ярким представителем первого агрегата является механическая коробка передач автомобиля. Второй вариант применяется в вариаторах.

Рассмотренные передаточные отношения передач рассчитываются на этапе проектирования агрегата при выборе кинематической схемы. С их помощью производится выбор типа соединения, определяется эффективность. Оценивается надёжность всего механизма.

Цепная передача

Хорошо известна цепная передача. Она относится к гибким конструкциям. Передаточное отношение цепной передачи рассчитывается расчёту зубчатых систем. Ведущая и ведомая звёздочка рассматриваются как зубчатые колеса. Значение этого параметра достигает 15.

Особенностью такой конструкции считается требование иметь определённое провисание цепи. Настройка этого параметра проводится с помощью специального регулирующего винта.

Достоинства подобного соединения сводятся к следующему:

К недостаткам можно отнести быстрый износ соединительных элементов цепи. Это требует периодической смазки. Вторым недостатком считается высокий уровень шума.

Кроме передаточного числа для них рассчитывается величина статистической разрушающей силы. Этот параметр зависит от требуемого коэффициента безопасности. Его задают в интервале от 6 до 10. Он обеспечивает качественную работу всего механизма, высокую надёжность соединения и долговечность.

Червячная передача

Необходимость изменения вращательного движения под углом требует создания специального вида систем. К таким конструкциям относится червячная передача. Основной элемент такой передачи может быть цилиндрической формы, глобоидным, эвольвентным, архимедовым винтом. Это зависит от поверхности, на которой расположена резьба, и профиля резьбы.

В качестве параметров, используемых для расчёта передаточного числа подставляемых в выражение, используют существующее количество заходов червячного механизма. Обычно оно варьируется от одного до четырёх. Таблица передаточных отношений для червячной схемы позволяет рассчитать необходимое количество элементов зацепления. Приведенные в этой таблице данные, помогают правильно выбрать соединения для конкретного механизма.

Основными недостатками передачи являются:

Ременная передача

Данная конструкция является часто встречающейся. Её тип определяется расположением вала и направлением движения ремня. Их классифицируют следующим образом:

Для повышения надёжности применяют спаренное соединение. Реализация подобных конструкций производится с помощью ремней различного сечения. Наиболее популярными являются три типа: прямоугольные, в форме трапеции, круглого сечения.

Значение передаточного отношения рассчитывается подстановкой в классическую формулу скоростей вращения ведущего и ведомого валов. Иногда в расчёте используют число оборотов каждого из валов. В качестве альтернативного варианта при расчёте этого параметра используются величины диаметров (радиусов) шкивов.

Источник

8.4: Передаточное отношение

Представьте себе велосипед: велосипедист обладает ограниченной мощностью, и хочет обеспечить максимальное использование этой мощности в любой момент времени.

Путем изменения механического преимущества изменяется скорость движения. Мощность представляет собой количество проделанной работы в единицу времени. Чем больше количество работы. тем ниже скорость ее выполнения.

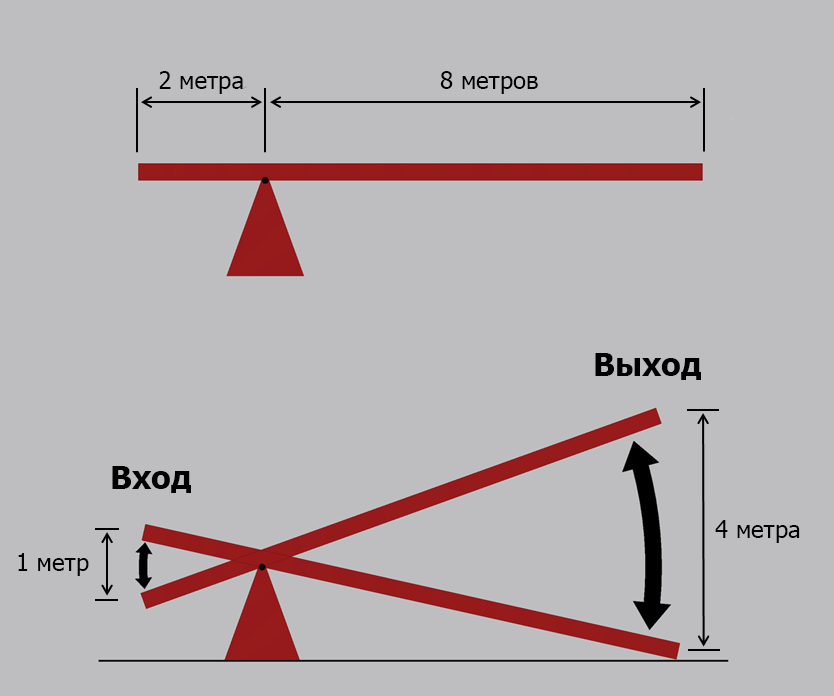
В примере 8.1 показано, что если на стороне входа рычаг сместится на 1 метр, на стороне выхода рычаг сместится на 4 метра. Разница пропорциональна соотношению между длинами рычагов.

Длина на выходе / Длина на входе = 8 / 2 = 4

Интересно то, что оба расстояния преодолеваются за одно и то же время. Давайте представим, что смещение рычага на входе на 1 метр происходит за 1 секунду, так что скорость движения на входе составляет 1 метр в секунду. В то же время, на выходе смещение на 4 метра также происходит за 1 секунду, так что скорость движения здесь составляет 8 метров в секунду. Скорость на выходе БОЛЬШЕ скорости на входе за счет соотношения между длинами рычагов.

В примере 8.2 представлена та же система, что и в примере 8.1, но теперь на вход действует сила, равная 4 ньютонам. Какова равнодействующая сила на выходе?

Прежде всего, необходимо рассчитать приложенный момент в центре вращения, вызванный входной силой, с помощью формул из Блока 7:

Крутящий момент = Сила х Расстояние от центра гравитации = 4 Н х 2 м = 8 Н-м

Далее, необходимо рассчитать равнодействующую силу на выходе:

Сила = Крутящий момент / Расстояние = 8 Н-м / 8 м = 1 ньютон

Глядя на эти два примера, мы видим, что если система смещается на 1 метр под действием входной силы, равной 4 ньютона, то на выходе она сместится на 4 метра под действием силы, равной 1 ньютон. При меньшей силе рычаг смещается быстрее!

Мы можем видеть, как механическое преимущество (выраженное в форме рычагов) может быть использовано для управления входной силой в целях получения требуемого выхода. Передачи работают по тому же принципу.

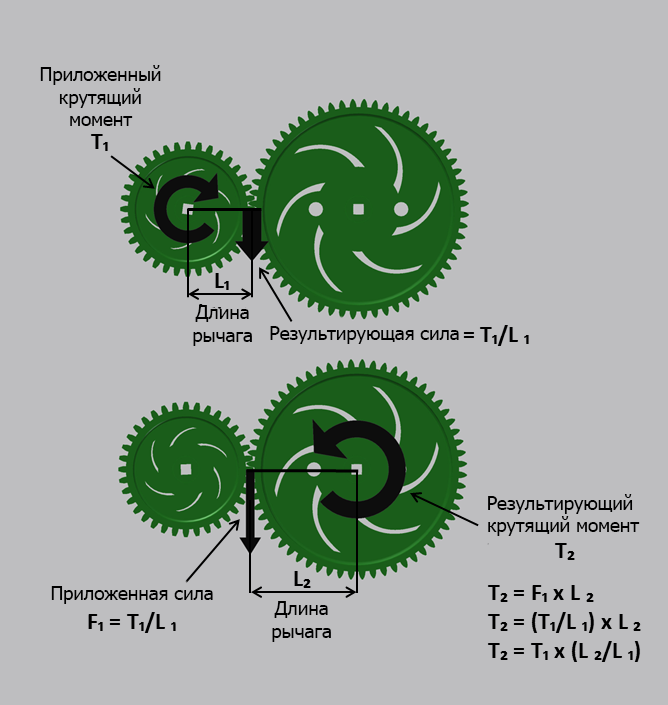
Цилиндрическая прямозубая шестерня по сути представляет собой серию рычагов. Чем больше диаметр шестерни, тем длиннее рычаг.

Как видно из примера 8.3, результатом крутящего момента, приложенного к первой шестерне, является линейная сила, возникающая на кончиках ее зубьев. Эта же сила воздействует на кончики зубьев шестерни, с которой зацепляется первая шестерня, заставляя вторую вращаться по действием крутящего момента. Диаметры шестерен становятся длиной рычагов, при этом изменение крутящего момента равносильно соотношению диаметров. Если малые шестерни приводят в движение больше шестерни, крутящий момент увеличивается. Если большие шестерни приводят в движение малые шестерни, крутящий момент уменьшается.

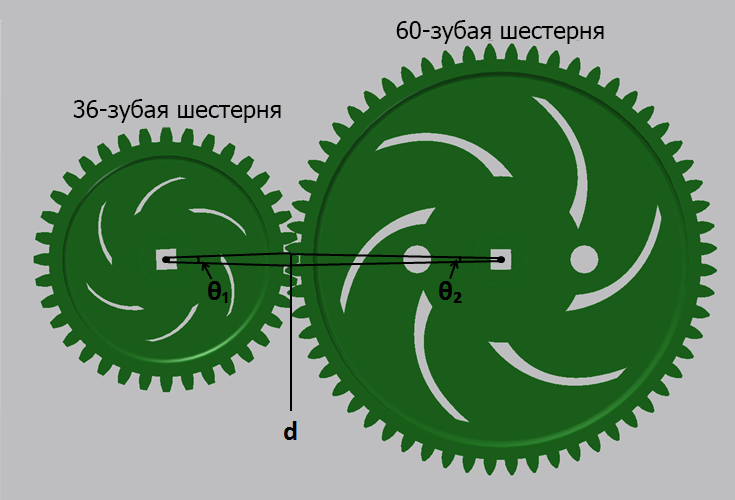
В примере 8.4, если входная 36-зубая шестерня поворачивается на расстояние одного зуба (d = ширина 1 зуба), это означает, что она поворачивается на 1/36-ю своего полного оборота (а1 = 360 / 36 = 10 градусов). Поворачиваясь, она приводит в движение 60-зубую шестерню, заставляя последнюю смещаться также на 1 зуб. Тем не менее, для 60-зубой шестерни это означает смещение всего лишь на 1/60-ю полного оборота (а2 = 360 / 60 = 6 градусов).

Когда малая шестерня проходит определенное расстояние в заданный интервал времени, большая шестерня при этом проходить меньшее расстояние. Это означает, что большая шестерня вращается медленнее малой. Этот принцип работает в обоих направлениях. Если малые шестерни приводят в движение больше шестерни, скорость понижается. Если большие шестерни приводят в движение малые шестерни, скорость повышается.

Как обсуждалось выше, количество зубьев шестерни прямо пропорционально ее диаметру, поэтому для расчета передаточного отношения вместо диаметра можно просто считать зубья.

Передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), поэтому представленная выше пара шестерен может быть описана как 12:60 (или 36 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = зубья ведомой шестерни / зубья ведущей шестерни = 60/36 = 1,67

Как обсуждалось выше, передаточное отношение выражается как (зубья ведущей шестерни) : (зубья ведомой шестерни), так что пара шестерен, представленная выше, может быть выражена как 12:60 (или 12 к 60).

Передаточное число рассчитывается по формуле (зубья ведомой шестерни) / (зубья ведущей шестерни)

Поэтому передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 60/12 = 5

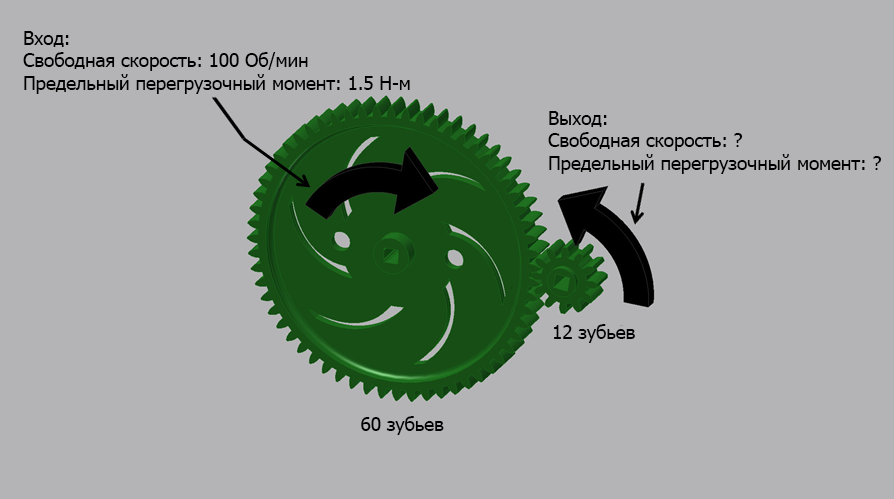
Глядя на пример, представленный выше.

Предельный перегрузочный момент второго вала может быть рассчитан по формуле:

Выходной момент = Входной момент х Передаточное число

Выходной момент = 1,5 Н-м х 5 = 7,5 Н-м

Свободная скорость второго вала может быть рассчитана по формуле:

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 5 = 20 об/мин

Второй вал, таким образом, вращается со свободной скоростью 20 об/мин, при этом предельный перегрузочный момент равен 7,5 Н-м. При понижении скорости крутящий момент увеличивается.

Для второго примера расчеты могут быть произведены тем же способом.

Передаточное число = Зубья ведомой шестерни / Зубья ведущей шестерни = 12/60 = 0,2

Выходной момент = Входной момент х Передаточное число = 1,5 Н-м х 0,2 = 0,3 Н-м

Выходная скорость = Входная скорость / Передаточное число = 100 об/мин / 0,2 = 500 об/мин

Второй вал, таким образом, вращается со свободной скоростью 500 об/мин, при этом предельный перегрузочный момент равен 0,3 Н-м. При повышении скорости крутящий момент уменьшается.

Источник

Определение передаточных отношений различных передач в теоретической механике

Определение передаточных отношений различных передач:

Передаточное отношение — основная кинематическая характеристика любой передачи.

Передаточные отношения определяются при помощи тех или иных геометрических элементов звеньев передачи. Найденное его значение выражает отношение угловых скоростей

Даны формулы, при помощи которых определяются передаточные отношения различных простейших передач, составленных из пары звеньев.

Передаточное отношение сложной передачи — передачи, составленной из нескольких простейших передач, равно произведению передаточных отношений простейших передач:

Передаточное отношение между двумя элементами передачи считается положительным, если оба элемента вращаются в одну сторону, например пара зубчатых колес с внутренним зацеплением.

Передаточное отношение между двумя элементами считается отрицательным, если оба элемента вращаются в противоположные стороны, например пара зубчатых цилиндрических колес с внешним зацеплением.

Задача №1

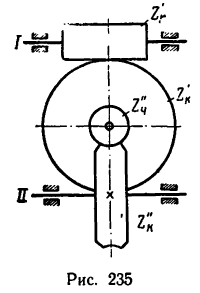
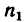
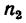
На каком расстоянии х необходимо установить каток 2 лобовой фрикционной передачи (см. эскиз к лобовой передаче в табл. 6), чтобы при угловой скорости = 400 об/мин катка 1 каток 2 вращался со скоростью = 500 об/мин? Диаметры катков

Определить также, какие наименьшую и наибольшую угловые скорости может получить вал катка 2 при различных положениях последнего.

1. Необходимое значение х (расстояние от катка 2 до оси катка I) найдем непосредственно из формулы передаточного отношения любой передачи:

2. Если начать передвигать каток 2 ближе к краю катка 1 (увеличить х), то точки на ободе катка 2 будут вступать в контакт с точками на торцовом поверхности катка 1, имеющими возрастающую скорость (по зависимостии в данном случае и благодаря силе трения станут приобретать такую же большую скорость.

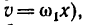
Если в выражение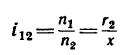
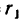
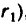
вместо х подставить наибольшее, теоретически возможное значение х — (практически xmas несколько меньше то

3. Если каток 2 установить у противоположного края катка 1, то угловая скорость у катка 2 также получится 10000 об/мин, но он будет вращаться в обратную сторону.

Таким образом, при

Благодаря способности изменять направление вращения вала, на котором укреплен каток 2, лобовую фрикционную передачу называют фрикционным вариатором (передача, способная варьировать направлением вращения).

4. При х = 0 (положение катка 2 совпадает с осью катка 1)

Точки на ободе катка 2 касаются практически неподвижных точек на торце катка 1 и поэтому не двигаются.

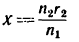
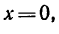
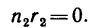
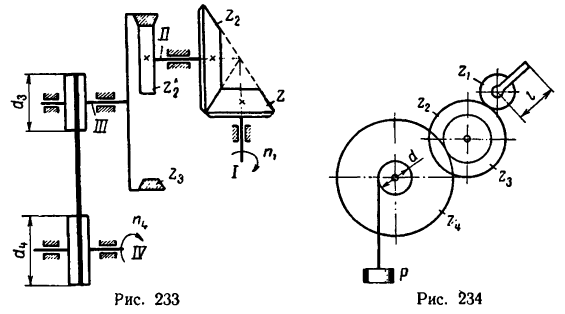
Иначе говоря, если в выражении принять то

Но так как

Задача №2

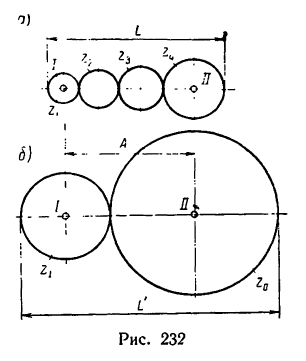
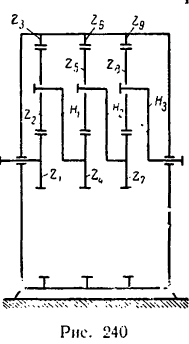
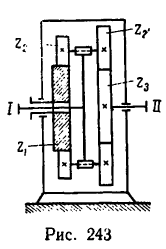
Передача вращательного движения между валами I и II осуществляется при помощи четырех зубчатых колес, два из которых помещены на промежуточных валах (рис. 232, а). Числа зубьев колес:

Модуль зубчатых колес m = 5 мм. Определить передаточное отношение межосевое расстояние А и габариты передачи L. Как изменятся габариты, если передачу осуществить при помощи лишь двух колес того же модуля?

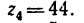
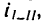
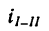
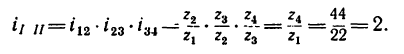
1. Передаточное отношениев данном случае равно произведению трех передаточных отношений между соседними колесами:

Как видно, зубчатые колеса, находящиеся на промежуточных осях, не влияют на величину передаточного отношения; поэтому их иногда называют «паразитными».

2. Находим межосевое расстояние А (см. рис. 232, а):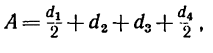

где 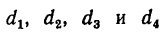— диаметры начальных окружностей зубчатых колес.

Подставляем вместо значений диаметров их выражения через модуль m и соответствующие числа зубьев:

3. Находим габариты передачи L (см. рис. 232, а):

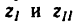
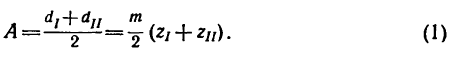
4. Если осуществить передачу при помощи двух колес с числами зубьев того же модуля, оставляя при этом межосевое расстояние передачи неизменным, то оно выразится так (рис. 232, б):

Здесь имеются два неизвестных 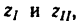но учтя, что передаточное отношение остается неизменным, получаем второе уравнение:

(как уже известно,

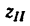
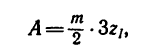
Подставим найденное значение в уравнение (1)

откуда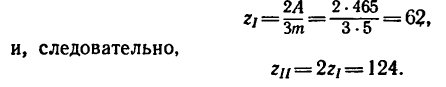

Теперь, зная число зубьев, легко определить габариты двухколесного варианта передачи:

Как видно, габариты увеличиваются на 300 мм, т. е почти в 1,5 раза (на 47,5%).

Отсюда следует сделать вывод, что при значительных межосевых расстояниях, которые по конструктивным причинам нельзя уменьшить, целесообразнее (для уменьшения габаритов) применять рядовое соединение нескольких зубчатых колес.

Задача №3

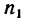
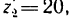
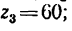
Какую угловую скорость л, нужно сообщить валучтобы при помощи передачи, показанной на рис. 233, вал IV вращался со скоростью —450 об/мин? Числа зубьев колес: коническихцилиндрическогос внутренним зацеплениемдиаметры шкивов

1. Передаточное отношение от вала I к валу IV равно в данном случае произведению трех передаточных отношений:

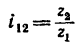
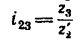
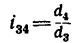
где — передаточное отношение конической зубчатой пары: г,

передаточное отношение цилиндрической пары с внутренним зацеплением;

— передаточное отношение ременной передачи.

После подстановки в эту формулу числовых значений получаем, что угловая скорость первого вала

Задача №4

Изображенный на рис. 234 механизм лебедки при вращении рукоятки, имеющей длину I, в вертикальном на-

правлении перемещает груз Р. Диаметр барабана d = 200 мм, число зубьев зубчатых колес механизма:

Определить: 1) с какой скоростью поднимается груз Р, если рукоятка / вращается с угловой скоростью я, =60 об/мин.

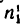
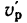
2) угловую скорость рукоятки, если груз должен подниматься со скоростью = 0,2 м/сек.

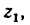
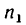
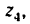
1. Если рукоятка l, жестко соединенная с колесом делает об/мин, то колесо а также жестко соединенный с ним бара бан получают в минуту число оборотов, равное

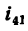
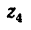
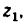
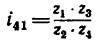
где— передаточное отношение от колеса к колесу причем и, следовательно,

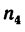
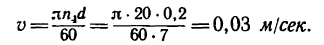
2. Так как барабан, вращаясь, делает об/мин, то окружная скорость точек на поверхности барабана
Скорость подъема груза Р равна окружной скорости и, следовательно,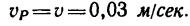

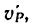
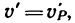
3. Если нужно поднимать груз со скоростью то и барабан должен вращаться так, чтобы его точки двигались с окружной скоростью при этом число оборотов в минуту барабана

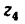
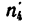
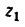
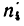
4. Если же барабан и вместе с ним колесо имеют об/мин, то колесо с рукояткой делают об/мин, причем

Такая угловая скорость рукоятки при ручном приводе, конечно, неосуществима.

Следующие две задачи рекомендуется решить самостоятельно.

Определение передаточных отношении простейших планетарных и дифференциальных передач

Планетарными называются передачи, в которых оси одного или нескольких колес закреплены в подвижном звене—водиле.

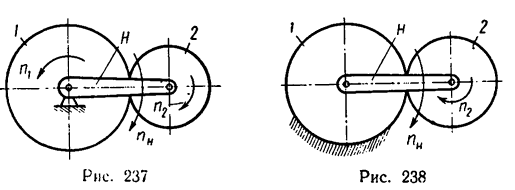
На рис. 237 показана схема передачи, состоящей из нейтрального колеса 1, сателлита 2 и водила H.

В общем случае центральное колесо и водило могут получать вращение от двух источников независимо друг от друга Такая

передача имеет две степени свободы и называется дифференциальной.

Если закрепить центральное колесо, то получается передача с одной степенью свободы — движение можно передавать либо от водила к сателлиту, либо от сателлита к водилу-• такая передача называется простой планетарной (рис. 238).

Чтобы в процессе решения задач глубже проанализировать кинематику планетарных передач, целесообразно не пользоваться готовыми выведенными в учебниках формулами, а применять метод сложения двух движений.

Сателлиты планетарных передач совершают сложное вращательное движение. Движение сателлитов относительно Земли (относительно неподвижной системы координат) складывается из вращения их вместе с водилом — переносного движения и вращения их вокруг осей, закрепленных в водиле, — относительного движения.

Метод сложения двух движений можно распространить и на центральные колеса. Так, например, закрепленное центральное жолесо простой планетарной передачи можно считать вращающимся вместе с воднлом и одновременно поворачивающимся на их общей оси в обратную сторону с такой же скоростью, что и водило.

Поэтому метод, который подробно изложен в решениях задач, включает следующие четыре этапа:

Введем такие обозначения:

-угловые скорости, выраженные в об/мин (рад/сек), зубчатых колес (центральных или сателлитов), дифференциальных передач, индексы соответствуют нумерации колес; — угловая скорость водила в дифференциальной передаче;

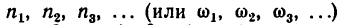
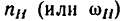
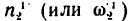
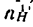
угловые скорости колес или водила в простой планетарной передаче (с закрепленным колесом) обозначим теми же буквами, но с верхними индексами в скобках, соответствующих закрепленному колесу, например— угловая скорость второго колеса при закрепленном первом;— угловая скорость водила при закрепленном первом и т. д.

Аналогично обозначим и передаточные отношения:

При решении задач с планетарными передачами необходимо очень внимательно следить за правильностью определения знаков передаточных отношений между отдельными элементами передачи.

Задача №5

Определить передаточное отношение от сателлита 2 к водилу Н для простой планетарной передачи, показанной на рис. 238, если числа зубьев колес

1. Осуществим первое движение. Закрепим колеса 1 и 2 на водиле и сообщим водилу вместе с колесами вращательное движение с угловой скоростью 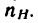Следовательно, в этом движении колеса 1 и 2 также получают угловую скорость

2. Осуществим второе движение. Освободим колеса от водила. Закрепим водило, т. е. превратим простую планетарную передачу в обычную зубчатую передачу, состоящую в данном случае из пары зубчатых колес.

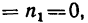
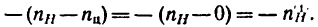
3. Угловая скорость центрального колеса в механизме так как колесо 1 закреплено. Поэтому во втором движении колесу 1 сообщаем скорость

В результате вращения колеса1 колесо 2 приобретет угловую скорость

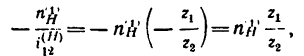
так как передаточное отношение от колеса 1, вращающегося со скоростью

ко второму колесу при закрепленном водиле отрицательное и равно

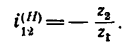
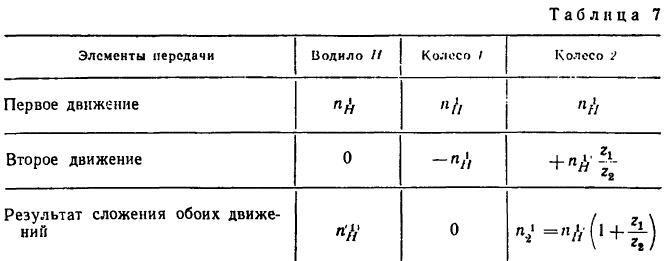
Приведенные результаты заносим в табл. 7, в нижней графе которой затем осуществляем третий этап — сложение обоих значений.

4. Находим передаточное отношение отсателлита 2 к водилу:

Таким образом,

Так как в данном случае передаточное отношение от колеса 2 к колесу 1 при закрепленном водиле имеет отрицательное значение

(a)

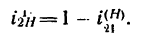
Но при помощи передачи, изображенной на рис. 238, неудобно передавать вращательное движение, так как необходимо дополнительное приспособление, чтобы сообщить угловую скорость сателлиту.

Аналогичная, но несколько видоизмененная простая планетарная передача рассматривается в следующей задаче.

Задача №6

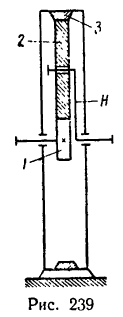
Определить передаточное отношение от колеса 2 к водилу Н простой планетарной передачи с закрепленным колесом внутреннего зацепления (рис. 239), если

1. Так же как и в предыдущей задаче, осуществим сначала первое движение, и тогда все элементы механизма (водило H, колеса 1,. 2 и 3) получат угловую скорость

2. Превратим планетарную передачу в обычную, закрепив водило. Освободим колеса и осуществим

4. Найдем передаточное отношение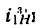

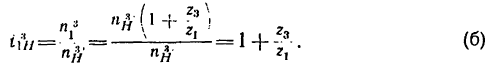
Подставим в (б) числовые значения чисел зубьев:

Таким образом, если к передаче подвести угловую скорость слева (к колесу 1), то справа (у водила Н) угловая скорость уменьшится в шесть раз.

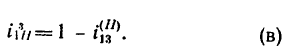
Сравнивая выражение (в) с выражением (а) из предыдущей задачи, замечаем, что они аналогичны.

Как видно, эти передачи не дают большого кинематического эффекта по сравнению с обычными передачами с неподвижными осями: передаточные отношения отличаются только на единицу.

Чтобы увеличить передаточное отношение, передачи, рассмотренные в задаче 202-40, соединяют последовательно.

Задача №7

Определить передаточное отношение 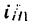для простой планетарной передачи, показанной на рис. 241, если числа зубьев колес

1. Осуществим первое движение (см. табл. 9).

2. Осуществим второе движение при закрепленном водиле, сообщив вращение колесу 3 (см. табл. 9).
3 Записав угловые скорости каждого элемента в первом и втором движении, сложим их (табл. 9).

4. Находим передаточное отношение

Особенно большим получается передаточное отношение, если

близко к единице. Так, например, при

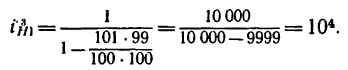
Следовательно, простая планетарная передача, состоящая всего из четырех колес, уменьшает угловую скорость в 10 тысяч раз.

Такие передачи создают большой кинематический эффект, но они имеют и крупный недостаток — крайне низкий коэффициент полезного действия (около 0,5%).

В следующей задаче рассматривается дифференциальная передача.

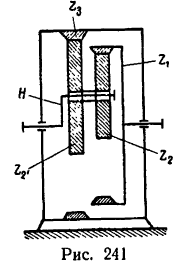
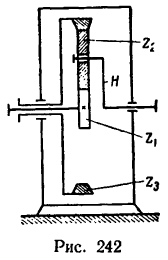
Задача №8

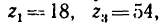
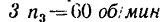
Определить угловую скорость водила Н и колеса 2 дифференциального зубчатого механизма (рис. 242), если число зубьев колес угловая скорость колеса = 120об/мин, угловая скорость колеса при направлении вращения в обратную сторону относительно колеса 1

1 Осуществим первое движение. Закрепив жестко все колеса на водиле, сообщим последнему угловую скорость 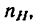тогда все три колеса получат ту же самую угловую скорость.

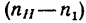
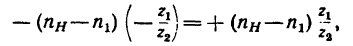
2. Освободив колеса от водила и закрепив его, сообщаем колесу 1 угловую скорость —об/мин. Тогда колесо 2 получит скорость

а колесо 3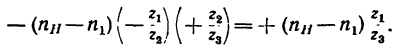

3. Сведем все результаты в табл. 10.

4. Число оборотов в минуту водила найдем из равенства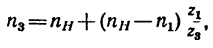

откуда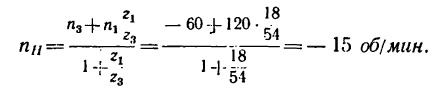

Водило И вращается с угловой скоростью 15 об/мин в ту же сторону, что и колесо 3.

5. Число оборотов в минуту колеса 2 определяем из равенства

но предварительно необходимо определить число зубьев

Из рис. 242 ясно, что

Так как модули всех колес равны между собой, то

откуда

и теперь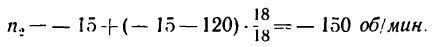
Таким образом, бегающее колесо (сателлит) вращается вокруг своей оси со скоростью 150 об/мин в ту же сторону, что и водило, и колесо 3.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник