параметры описывающие форму оригинала называют параметрами

Параметры описывающие форму оригинала называют параметрами

DELETED запись закреплена

Контрольные вопросы и задания
1. Покажите, что познавательная и преобразовательная деятель ности субъекта невозможны без моделирования.

Начнем с преобразовательной. Что бы человек ни делал, изменяя реальность, еще до начала самой работы он должен определить цель, образ желаемого будущего, т.е. модель того, чего пока
нет, но что хотелось бы осуществить, что должно появиться в конце работы. Это первый аргумент о необходимости моделирования. Но это еще не все: для достижения конечного результата необходимо выполнить определенную последовательность промежуточных действий, а для того, чтобы их правильно выполнить, нужно еще до начала работы описать эту последовательность, т.е. создать модель (план, алгоритм) хода работы. Таким образом, преобразовательная (трудовая, управленческая) деятельность невозможна без моделирования.
Теперь о познавательной деятельности. Конечный результат познания — полученная информация о внешней среде — должен быть зафиксирован, описан, представлен в виде определенной модели. Знания вообще существуют только в форме моделей, т.е. модель есть форма существования знаний. Конечной целью познания является построение моделей интересующей нас части мира. Но не только поэтому познание невозможно без моделирования. Важно также, что и сам процесс получения информации извне происходит с помощью специальных моделей. Это только кажется, что стоит открыть глаза и информация сама хлынет через них. Во всех языках различаются понятия «смотреть» и «видеть». Можно смотреть и не увидеть, можно видеть то, чего на самом деле нет. Врач, осматривающий пациента, обращает внимание на такие внешние признаки, которые ничего не говорят неспециалисту. С помощью гипноза или использования эффектов обмана зрения можно заставить человека увидеть несуществующее. Все это происходит благодаря тому, что информация световых сигналов обрабатывается нашими моделями, прежде чем достичь состояния, осознаваемого как зрительный образ. Это относится не только к зрению, но и ко всем остальным чувствам, являющимся каналами связи субъекта со средой. Необходимо напомнить, что субъект одновременно является объектом. Объект «напрямую» взаимодействует со средой, а субъект — только через модели. Например, потрогав горячую плиту, вы обожжетесь как объект. Но если подменить ваши модели гипнозом или наркотиком, вы не будете ничего чувствовать. Еще более нагляден известный психологический опыт, когда у человека, убежденного, что утюг горячий, возникает ожоговый волдырь после прикосновения к нему, хотя на самом деле утюг холодный.
Итак, любая деятельность субъекта, любое его взаимодействие с внешним миром происходят посредством моделей, хотя как объект он непосредственно связан с окружающей средой (рис. 2).

2. Опишите алгоритм анализа и перечислите, какие модели он по рождает.

Процедура анализа состоит в последовательном выполнении следующих трех операций:
1) сложное целое расчленить на более мелкие части, предположительно более простые;
2) дать понятное объяснение полученным фрагментам;
3) объединить объяснение частей в объяснение целого.
Если какая-то часть системы остается все еще непонятной, операция декомпозиции повторяется и мы вновь делаем попытку объяснить новые, еще более мелкие фрагменты

Первым продуктом анализа является, как это видно из схемы, перечень элементов системы, т.е. модель состава системы.

Вторым продуктом анализа является модель структуры системы.

Третий продукт анализа — модель черного ящика для каждого элемента системы.

Итак, в результате анализа мы получаем информацию об устройстве и работе системы. Вся полученная информация «упакована» в виде всех трех типов моделей: состава, структуры, черного ящика.

3. Опишите алгоритм синтеза и укажите, какие модели он порож дает. Какая из них непосредственно описывает исследуемый объект (явление)?

Ответы на вопросы такого рода дает синтез.
Синтетический метод состоит в последовательном выполнении трех операций:
1) выделение большей системы (метасистемы), в которую интересующая нас система входит как часть;
2) рассмотрение состава и структуры метасистемы (ее анализ);
3) объяснение роли, которую играет наша система в метасистеме, через ее связи с другими подсистемами метасистемы (рис. 4).
Конечным продуктом синтеза является знание связей нашей системы с другими частями метасистемы, т.е. модель черного ящика. Но чтобы ее построить, нам пришлось попутно создать модели состава и структуры метасистемы как побочные продукты. И снова мы видим, что все полученные нами знания «упакованы» в три известных формы моделей: черного ящика, состава и структуры. Ясно, что качество синтеза напрямую зависит от качества модели метасистемы,
о чем следует особо позаботиться.

4. Что такое абстрактная модель? Кроме языковых, какие еще при меры абстрактных моделей вы можете привести?

5. Чем вызвано многообразие языков?

6. Какова простейшая абстрактная модель разнообразия окружаю щей нас реальности?

Классификация — простейшая абстрактная модель разнообразия реальности
Пожалуй, главное назначение языка — описывать, отображать бесконечно разнообразный мир. В мире нет абсолютно одинаковых объектов. Даже если считать, например, электроны тождественными по своим электрическим и механическим свойствам (хотя имеются основания утверждать, что это не совсем так: закон их распределения, выведенный из предположения об их идентичности, в эксперименте не совсем точно выполняется) — они отличаются хотя бы координатами. Как же описывать бесконечно разнообразный мир конечными фразами? Выход один — делать это огрубленно, приблизительно, упрощенно.
Первый шаг упрощения основан на том, что все объекты различны, но одни отличаются друг от друга «слабо», «мало», «незначительно», другие — «сильно», «существенно» (обратите внимание на оценочность этих терминов). Идея теперь состоит в том, чтобы объединить все мало различающиеся объекты в одну группу, оставив вне ее все сильно различающиеся.
Второй шаг упрощения состоит в том, чтобы отказаться от учета различий внутри группы, пренебречь малыми отличиями, считать членов группы одинаковыми. Такую группу принято называть классом.
Оставшиеся вне класса объекты тоже разнообразны, и хотя «сильно» отличаются от тех, которые вошли в класс, по некоторым другим признакам снова оказываются между собой «похожими» либо
«различными». Это дает возможность выделить новые классы похожих внутри них и отличающихся от других классов.
В итоге бесконечно разнообразный мир описывается конечным множеством отличающихся друг от друга классов.
Для выражения различий между классами им присваиваются различные имена (названия, обозначения, символы, номера и т.п.). Эти имена и есть слова некоторого языка. Деревья (все деревья), животные (тоже все), люди, здания, насекомые, реки и т.д. — примеры имен классов. Классифицировать можно не только объекты, но и свойства (цвета, звуки, силы, размеры и т.д.), и процессы (ходить, бегать, тянуть, есть, пить и т.д.). Таким образом, слова языка есть названия некоторых классов. Классификация есть простейшая абстрактная модель разнообразия действительности.
Распознавание, идентификация объекта в данном случае состоит в выяснении того, к какому классу он принадлежит (какое имя он должен носить).
При построении моделей субъект имеет простор для неформальных, творческих действий.
Во-первых, необходимо выбрать характеристику, параметр, меру различия между объектами. Множественность характеристик является одной из причин множественности классификаций. Особый (и нетривиальный) вопрос — классификация не по одному, а по нескольким признакам.
Во-вторых, от конкретизации оценочных понятий «слабых» и «сильных» различий зависят число различаемых классов и задание границ между ними.
Важно помнить, что любая классификация есть только модель разнообразия реальности, что реальность более сложна, что всегда найдется объект, который нельзя однозначно отнести к тому или иному классу.

7. Чем отличаются искусственная и естественная классификации?

Искусственная и естественная классификации
Различают два вида классификаций: искусственную и естественную.

При искусственной классификации разделение на классы производится «так, как надо», т.е. исходя из поставленной цели — на столько классов и с такими границами, как это диктуется целью. Например (это научные данные), крестьянские семьи в 20-е гг. XX в. в Сибири отличались по зажиточности q согласно «колоколообразному» распределению (рис. 8) — таково было их разнообразие. Для некоторых целей было введено разделение крестьян на три класса:
бедняки, середняки, кулаки, что упрощенно описывало их разнообразие. Однажды на основе этой модели большевики поставили задачу «ликвидировать кулачество как класс» и реализовали эту цель.
Характерно, что граница между классами была определена нечетко, что только усилило произвол. Не зря искусственную классификацию называют еще произвольной.

8. Что называется реальной моделью? Приведите три типа реаль ных моделей (классификацию по происхождению подобия модели оригиналу).
Реальные модели
Второй класс моделей образуют реальные предметы, используемые в качестве моделей. Аналитический прием классификации по происхождению подобия между моделью и оригиналом приводит к трем типам реальных моделей.

Первый тип назовем моделями прямого подобия. Прямое подобие между моделью и оригиналом устанавливается вследствие их непосредственного взаимодействия (следы, отпечаток пальца, печать и т.д.) либо вследствие цепочки таких взаимодействий (фотография, макет здания и т.п.).

Второй тип — модели косвенного подобия, или аналогии. Похожесть, аналогичность двух явлений объясняется совпадением закономерностей, которым они подчиняются. Абстрактные модели (теории) двух явлений могут «перекрываться», а это приводит к похожести данных явлений. Поэтому наблюдая одно из них, можно высказать суждение о другом (см. рис. 12: O — «объект», M — «модель»). Примером служит электромеханическая аналогия: закон Ньютона F = m·a и закон Ома U=R.I структурно идентичны. Это дает возможность отображать механические системы электрическими, с которыми проще, удобнее работать. В тело многих зданий и сооружений (мостов, башен) закладываются пьезодатчики, соединенные с электрической моделью сооружения. Это позволяет судить о его состоянии и принимать решение об обслуживании. Другие примеры аналогий — подчиненность закону Кирхгофа токов в электросетях, потоков воды в трубопроводах, информации в сетях связи, транспорта на улицах города. На электрической модели можно отрабатывать оптимальные структуры и управление для соответствующих сетей. Моделями косвенного подобия являются: аналоговые ЭВМ, следственный эксперимент в криминалистике, исторические параллели, жизни разлученных однояйцовых близнецов, подопытные животные в медицине и т.д.
Однако следует осторожно пользоваться аналогиями, поскольку, кроме совпадающих закономерностей, у разных явлений есть и несовпадающие. Поэтому не все заключения о модели можно переносить на оригинал, не все особенности оригинала содержатся в модели — аналоге. Иногда вводится понятие «сила аналогии», связанное со степенью «перекрытия» сравниваемых теорий.

Третий тип реальных моделей основан на подобии, которое не является ни прямым, ни косвенным. Например, буквы — модели звуков; деньги — модели стоимости; различные знаки, сигналы, символы, карты, чертежи содержат соответствующую информацию. Соответствие такой модели и оригинала устанавливается в результате соглашения между ее пользователями, носит культуральный, условный, информационный характер. Назовем такие модели моделями условного подобия. Они успешно работают, но лишь до тех пор, пока известны и соблюдаются договоренности, соглашения о их значении (денежная реформа, мертвые языки, секретные знаки и т.п.).

9. Чем отличается использование познавательных и прагматичес ких моделей?

10. Почему в любой модели есть, кроме истинного, и (обязательно и неизбежно) неистинное содержание?

Продолжая рассмотрение отношений между моделью и оригиналом, остановимся на содержании информации в модели. Оригинал и модель — разные вещи. В оригинале есть много такого, чего нет в модели, по двум причинам: во-первых, не все из того, что известно об оригинале, понадобится включить в модель, предназначенную для достижения конкретной цели (зона А на рис. 13 изображает известное, но ненужное, в том числе ошибочно сочтенное ненужным и не включенное в модель); во-вторых, в оригинале есть всегда нечто непознанное, поэтому не могущее быть включенным в модель (зона В на рис. 13). Зона 2 на рисунке изображает информацию об оригинале, включенную в модель. Это истинная информация, то общее, что имеется у модели и оригинала, благодаря чему модель может служить его (частным, специальным) заменителем, представителем. Обратим внимание на зону 3. Она отображает тот факт, что у модели всегда есть собственные свойства, не имеющие никакого отношения к оригиналу, т.е. ложное содержание. Важно подчеркнуть, что это относится к любой модели, как бы ни старался создатель модели включать в нее только истину.

Рис. 13
Например, аналитическая функция времени как модель сигнала отображает тот факт, что сигнал — это некоторый временной процесс. Но эта модель не отражает того, что повторный сигнал уже не несет той информации, что в первый раз. Эта модель не обладает свойством реальных сигналов одновременно занимать конечный интервал времени и конечную полосу частот. Во многих (а если присмотреться — во всех) теориях особенность модели содержать ложную информацию проявляется в виде так называемых парадоксов. Например, в теориях электростатики и гравитации парадоксы бесконечности возникают при нулевых расстояниях.
Прагматические модели обслуживают процессы преобразования реальности в соответствии с целями субъекта. Они отображают пока несуществующее, но желаемое (проекты, планы, программы, алгоритмы, нормы права и т.д.), и имеют нормативный, директивный характер. Это придает им статус «единственно верных», что ярко выражено в религиях, морали, стандартах, технических чертежах, технологиях и т.д. В отличие от познавательных моделей, «подгоняемых» к реальности, в преобразовательной деятельности реальность «подгоняется» под прагматическую модель (рис. 14).

Рис. 14
Закончим рассмотрение отношений между оригиналом и моделью подчеркиванием неточности, приблизительности модели. Даже те аспекты оригинала, которые намеренно отображаются,
описываются с некоторой точностью, приближенно. Иногда приблизительность носит вынужденный характер (нехватка знаний), а иногда вводится сознательно, ради упрощения работы с моделью (например, линеаризация нелинейных отношений между переменными).
11. Какое качество модели называется адекватностью?

12. Что является окружающей средой для модели?

13. Проверьте, запомнили ли вы определения приведенных ниже терминов. Их знание позволит вам пользоваться профессиональным языком системного анализа.
Модель. Анализ. Синтез.
Модель абстрактная. Модель языковая. Модель реальная.
Классификация (искусственная и естественная).
Модели познавательные.
Модели прагматические.
Адекватность модели
Культура (субъекта, организации, нации – любой социаль ной системы).

Задание 1:
Рассмотрите следующие организации:
• университет;
• магазин;

Источник

Определение параметров формы и положения кривых 2-го порядка

Дата публикации: 22.02.2017 2017-02-22

Статья просмотрена: 865 раз

Библиографическое описание:

Мурадов, Ш. К. Определение параметров формы и положения кривых 2-го порядка / Ш. К. Мурадов, М. К. Халимов, З. Э. Мирзалиев, Г. С. Рамазанова. — Текст : непосредственный // Молодой ученый. — 2017. — № 7 (141). — С. 454-457. — URL: https://moluch.ru/archive/141/39580/ (дата обращения: 12.11.2021).

В настоящей статье рассматриваются определения формы и положения кривых 2-го порядка на плоскости и в пространстве, которые применяются для задания этих кривых и для определения положения плоскостей пересекающих поверхностей 2-го порядка по заданному коническому сечению.

Ключевые слова: прикладная геометрия, инженерная графика, графические дисциплины, кривые 2-го порядка, эллипс, гипербола, парабола, окружность, параметры, положения, формы, параметрическая мощность, центр

Многие годы в Ташкентском государственном педагогическом университете Республики Узбекистан подготавливаются магистры по специальности — 5А110802 — Инженерная графика и теория дизайна. В связи с этим в ТГПУ имени Низами как головной педагогический университет систематически совершенствуются типовые учебные и тематические планы по дисциплине «Прикладная геометрия» с новыми требованиями. При этом особенно уделяются внимание методам исследования кривых линии и поверхностей, которые часто встречаются на различных отраслях производства, как в машиностроении, так и в сооружениях строительства. Как известно, пространство заполнено множеством геометрических фигур для выделения из них определенных фигур требуется некоторые дополнительные условия. Например, определение параметров положения и формы геометрических фигур отвечающим наперед заданным условиям. Образование и построение кривых линии 2-го порядка часто встречаются в учебном процессе для построения линии пересечения кривых поверхностей 2-го порядка с плоскостью и между собой. Поэтому вопрос определения параметров положения и формы кривых линии 2-го порядка имеют особое место для преподавания графических дисциплин.

Параметры, определяющие положения кривых 2-го порядка называем параметрами положения кривых 2-го порядка. Параметры, определяющие вид (форму) кривых 2-го порядка, называются параметрами формы этих кривых.

В настоящей статье рассматривается один из способов определения параметров положения и формы кривых линии 2-го порядка, как на плоскости, так и в пространстве.

2.1. Параметры положение произвольной параболы на плоскости можно определить заданием её вершины (или фокуса) и направлением оси параболы (рис. 3). Задание вершины параболы (точка) на плоскости определяется двумя параметрами, заданием направления оси параболы определяет еще один параметр. Следовательно, число параметров положения произвольной параболы на плоскости равно трем. Совокупность парабол на плоскости четырех параметрическое множество, мощность которого равна ∞ 4 (один — параметр формы. Три — параметры положения).

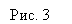
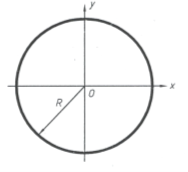
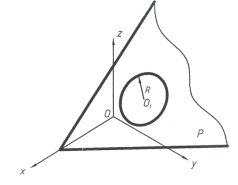
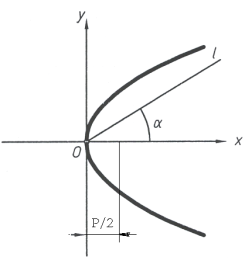
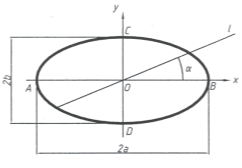
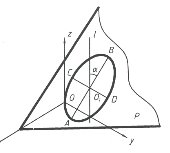
Известно, что из кривых второго порядка эллипс и гиперболы относятся к группе центральных кривых. Они имеют центр (точка) и главные оси, которые определят формы этих кривых. Поэтому определение параметров формы и положения эллипса и гиперболы будим рассматривать аналогично.

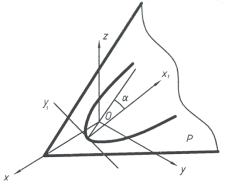
Выше приведенные соображения можно использовать для задания кривых 2-го порядка и для определения положения плоскостей пересекающих поверхности 2-го порядка по заданному коническому сечению.

Необходимо отметить, что изучая способы образования и задания некоторых других кривых более высокого порядка, можно определить число параметров формы и положение этих кривых.

Выше приведенные сведения для определения количество параметров формы и положения кривых 2-го порядка как на плоскости и в пространстве можно определить по таблице № 1.

Источник

Параметры и характеристики

Количественно любая система описывается совокупностью величин, которые могут быть разбиты на два класса:

• параметры, описывающие первичные свойства системы и являющиеся исходными данными при решении задач анализа;

• характеристики, описывающие вторичные свойства системы и определяемые в процессе решения задач анализа как функция параметров, то есть эти величины являются вторичными по отношению к параметрам.

Множество параметров технических систем можно разделить на:

• внутренние, описывающие структурно-функциональную организацию системы, к которым относятся:

— структурные параметры, описывающие состав и структуру системы;

— функциональные параметры, описывающие функциональную организацию (режим функционирования) системы.

• внешние, описывающие взаимодействие системы с внешней по отношению к ней средой, к которым относятся:

— нагрузочные параметры, описывающие входное воздействие на систему, например частоту и объем используемых ресурсов системы;

— параметры внешней (окружающей) среды, описывающие обычно неуправляемое воздействие внешней среды на систему, например помехи и т.п.

Параметры могут быть:

• детерминированными или случайными;

• управляемыми или неуправляемыми.

Характеристики системы делятся на:

• глобальные, описывающие эффективность системы в целом;

• локальные, описывающие качество функционирования отдельных элементов или частей (подсистем) системы.

К глобальным характеристикам технических систем относятся:

• мощностные (характеристики производительности), описывающие скоростные качества системы, измеряемые, например, количеством задач, выполняемых вычислительной системой за единицу времени;

• временные (характеристики оперативности), описывающие временные аспекты функционирования системы, например время решения задач в вычислительной системе;

• надежностные (характеристики надежности), описывающие надежность функционирования системы;

• экономические (стоимостные) в виде стоимостных показателей, например, стоимость технических и программных средств вычислительной

системы, затраты на эксплуатацию системы и т.п.;

• прочие: масса-габаритные, энергопотребления, тепловые и т.п.

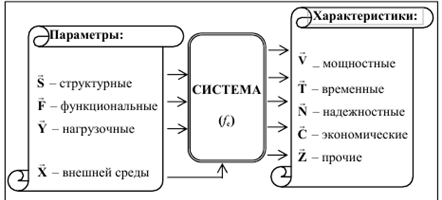
Таким образом, параметры системы можно интерпретировать как некоторые входные величины, а характеристики – выходные величины, зависящие от параметров и определяемые в процессе анализа системы

Рис.2. Параметры и характеристики системы

Тогда закон функционирования системы можно представить в следующем виде:

,

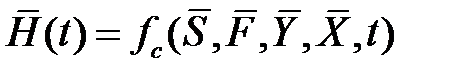
где f_с – функция, функционал, логические условия, алгоритм, таблица или словесное описание, определяющее правило (закон) преобразования входных величин (параметров) в выходные величины (характеристики);H(t) –вектор характеристик, зависящий от текущего момента времени t

.

Источник

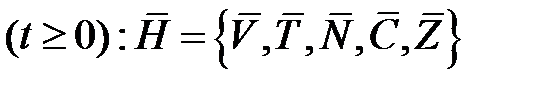
Параметр (техника)

Технический пара́метр — физическая величина, характеризующая какое-нибудь свойство технического устройства, системы, явления или процесса. Число, характеризующее этот параметр (величину), является его значением.

Параметр — это обобщенное название определенного физического, геометрического или иного свойства устройства (процесса). Это могут быть, например, размер, скорость, напряжение и т. д. Изучением видов параметров, измерений, методов и средств обеспечения их единства и способов достижения требуемой точности занимается метрология.

Содержание

Виды технических параметров

Параметры подразделяются на входные, внутренние и выходные.

Входные (внешние) параметры отражают внешние требования к техническому устройству (процессу), их значения или характер изменения с той или иной точностью известны. Часть этих параметров, существенно влияющих на состояние и характеристики устройства (процесса), называют управляющими.

Часть входных параметров, которые характеризуют выполняемую устройством (процессом) функцию, относят к функциональным параметрам. Эти параметры в процессе проектирования известны.

Внутренние параметры характеризуют состояние и свойства самого устройства (процесса). Их значения определяются или уточняются в процессе проектирования. Они необходимы для обоснования принимаемых решений, характеристики свойств устройства и других целей.

Часть входных параметров и рассчитанных внутренних параметров устройства (процесса) может использоваться в качестве исходных данных для другого, взаимосвязанного устройства (процесса) или его модели. Такие параметры называются выходными параметрами для рассмотренного устройства (процесса) и входными — для вновь рассматриваемого.

Например, для устройства «лифт» входными параметрами будут, например, масса груза (функциональный параметр) и высота его подъёма, срок службы (они задаются, приходят извне), а внутренними, например, диаметр и материал троса, размеры кабины лифта (они определяются, характеризуют устройство и вначале неизвестны). Для устройства «шахта лифта» ранее найденные размеры кабины лифта будут входными параметрами и, следовательно, — выходными параметрами для устройства «лифт».

Некоторые параметры могут выступать в виде обобщённых параметров, объединяющих в себе ряд свойств. Эти параметры применяют, когда излишняя конкретизация при решении задачи не требуется, либо вызывает потребность в дополнительных специальных знаниях. Однако при таком параметре должна быть ссылка на документ, однозначно раскрывающий его содержание.

Например, марка (название) материала: сталь 45 ГОСТ 1050-88 «Прокат сортовой, калиброванный, со специальной отделкой поверхности из углеродистой качественной конструкционной стали. Общие технические условия». Она содержит данные о составе, условиях изготовления и иных свойствах материала и является обобщённым параметром, скажем, для проектировщика, но не для материаловеда или металлурга.

В зависимости от того, что характеризуют параметры — реальное устройство (процесс) или его модель, параметры подразделяют на нормированные и действительные.

Нормированный параметр

Нормированный параметр (или, более правильно, нормированное значение параметра) — это теоретическая величина, значение которой устанавливается нормативно-техническими документами и характеризует признаки модели соответствующего технического устройства. Выражается предельными допустимыми значениями параметра. Изделие, параметры которого будут находиться внутри интервала, образованного этими предельно-допустимыми значениями, считается работоспособным и может использоваться по назначению.

Например, длина стержня, указанная на чертеже, составляет 98…104 мм. Это — нормированное значение параметра, установленное чертежом, а 98 и 104 — предельно-допустимые его значения (наименьшее и наибольшее предельно-допустимые значения параметра).

Если одно из предельных значений равно нулю или бесконечности, то оно не указывается, а подразумевается. Например, твёрдость поверхности детали не менее НВ180, что означает 180…∞. Или, например, поднимаемый груз — 200 кг, что соответствует 0…200.

Для марки материала, например, стали, предельно-допустимые значения содержатся в соответствующем ей ГОСТе.

Величина интервала, ограниченного предельными значениями параметров, называется допуском параметра. Он обозначается буквой T (в предыдущем примере Т = 104–98 = 6 мм). Сама же область допустимых значений параметров называется полем допуска.

Действительный параметр

Действительный параметр (или действительное значение параметра) характеризует признаки конкретного реального изделия. Его определяют путем испытаний [1] или измерительного эксперимента с точностью, достаточной для контроля этого параметра.

Обычно каждое замеренное действительное значение уникально, так как его величина зависит от внешних условий, условий изготовления, способа и точности измерения и многих других факторов. С целью повышения достоверности знания значения параметра проводят ряд измерений, результаты которых будут иметь разброс внутри какого-то интервала. По этой причине действительное значение параметра задают диапазоном. Совпадение действительных значений одних и тех же параметров изделий из их партии возможно только в пределах точности измерения.

Например, измерениями была установлена длина стержня 97…98 мм. Это — действительное значение параметра, истинное значение которого лежит внутри диапазона, заданного суммарной погрешностью измерения. Повышение точности измерений сузит данный диапазон, например, до 97,6…98,1 мм.

Точность оценивается погрешностью измерения, которая представляет собой разность между действительным и истинным значениями параметра. За истинное значение параметра принимается идеальное значение, к которому стремится действительное значение параметра при повышении точности измерения. Истинное значение не может быть определено экспериментально, поскольку все средства измерения имеют некоторую погрешность измерения. Вместо истинного значения для оценки погрешности измерения берут действительное значение параметра, определенное другим средством измерения, погрешность которого на порядок меньше допустимого значения для данной цели.

Погрешность измерения включает в себя составляющие, причинами возникновения которых являются средства измерения, метод измерения и оператор (субъект).

Номинальный параметр

Для удобства записи параметров используют номинальный [2] параметр (номинальное значение параметра), то есть такое его значение, которое служит началом отсчета действительных и предельно допустимых отклонений. Субъективно назначается человеком либо является результатом операций с такими же номинальными параметрами.

Например, длину стержня, указанную на чертеже, можно записать как 101±3 мм. Здесь 101 — номинальное значение, ±3 — отклонения, задающие предельные значения параметра (98…104). В приведенном примере номинальное значение выбрано из середины интервала и, как следствие, отклонения будут симметричными. Если в качестве номинального значения принять «круглую» величину 100, то форма записи данного нормированного параметра примет, например, следующий вид , где +4 — величина верхнего предельного отклонения (100+4), −2 — нижнего (100+(-2)).

Номинальным параметром можно считать марку материала, приведённую без ссылки на соответствующий ГОСТ, например, сталь 45.

Часто оперируют только с номинальными значениями параметров, например, указывают длину стержня как 100 мм. Решать уравнения с параметрами, заданными в таком виде, удобнее, хотя теряется ощущение точности не только исходных данных, но и результата вычислений.

Однако изделие считается годным, если действительные значения его параметров попадают в интервал, задаваемый предельными значениями нормируемого параметра. Если указано только номинальное значение нормируемого параметра, то формально значение интервала равно нулю и попасть в такой интервал практически невозможно и, следовательно, каждое изделие по этому параметру будет бракованным. Поэтому в документации (особенно предназначенной для других пользователей — заказчика, исполнителя, покупателя, других специалистов) принято приводить нормированные значения параметров, а не указывать только их номинальные значения.

Для устранения излишнего многообразия номинальных значений параметров их рекомендуют нормировать, то есть приводить в соответствие (например, округлять расчетные значения) с предпочтительными числами.

Оценка значения технического параметра

Значения параметров могут оцениваются следующим образом:

Источник