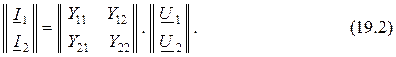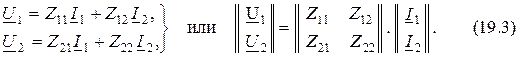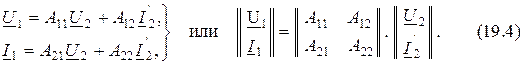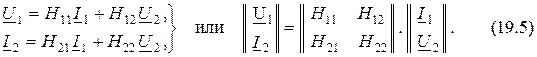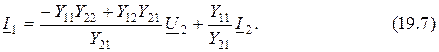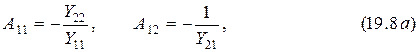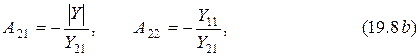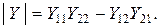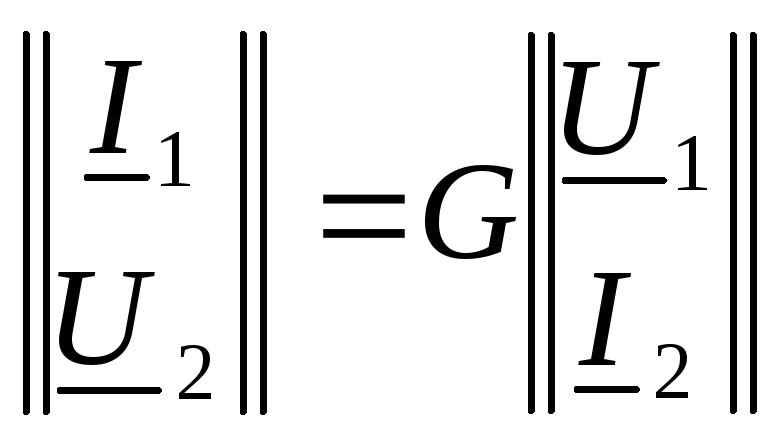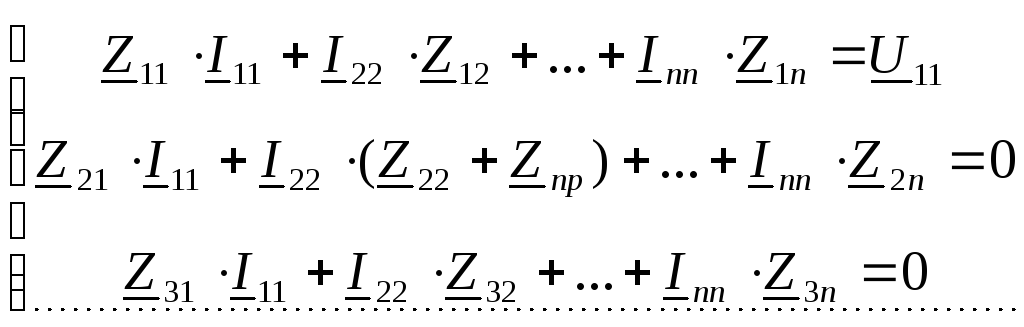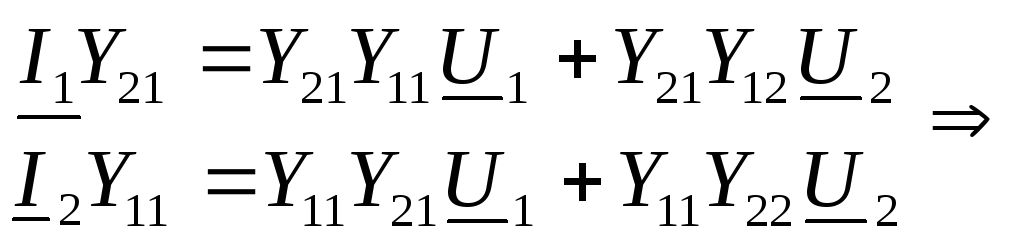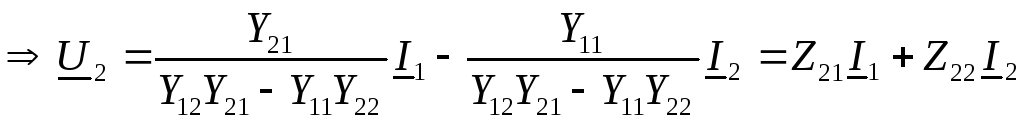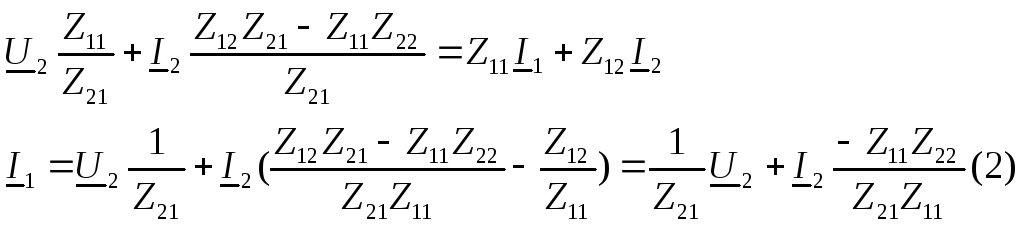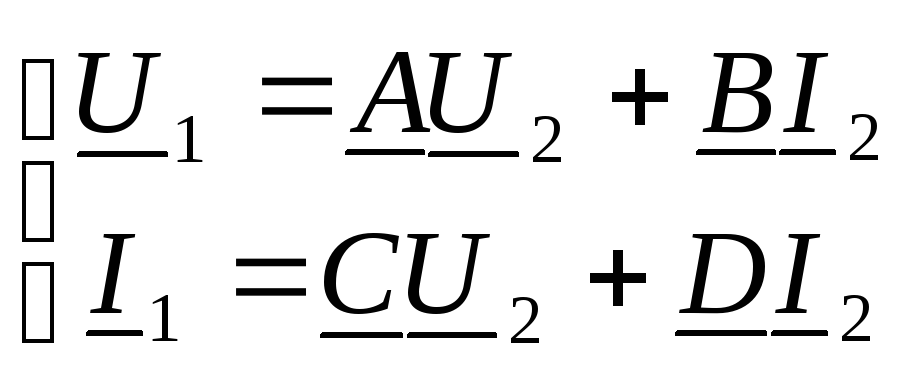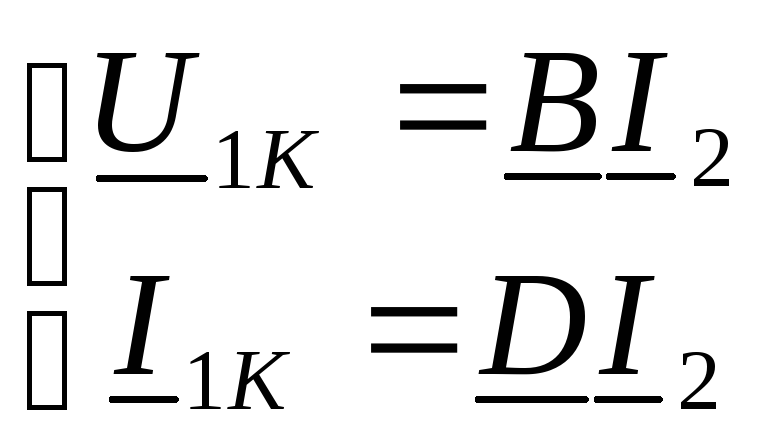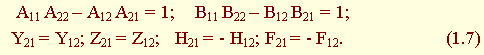параметры четырехполюсника в форме а

08.07.202209.07.2022 admin 0 Comments

Системы уравнений четырёхполюсников

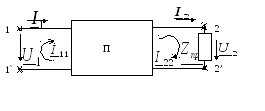
Рис. 19.1. Четырёхполюсник – общее обозначение

Схемы замещения четырёхполюсников

Коэффициенты уравнений четырёхполюсников

Системы уравнений четырёхполюсников

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ЧЕТЫРЁХПОЛЮСНИКОВ

ЛЕКЦИЯ 19

План лекции:

19.1. Основные определения и классификация четырёхполюсников

Электрическую цепь или её часть, рассматриваемые относительно двух пар выводов, называют четырёхполюсником (рис. 19.1).

Входную (первичную) пару выводов четырёхполюсника обозначают цифрами 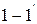, выходную (вторичную) – . В качестве положительных принимают направления напряжений от верхних выводов к нижним, а токов – втекающими. В отдельных случаях положительными считают вытекающие токи. Вариант с положительными токами и называют прямой передачей, и – обратной, втекающими токами и – комбинированной. Сочетание токов и специального названия не имеет и применяется редко.

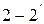
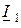
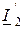
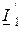
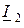
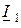
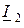
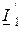
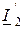
В случае гармонических сигналов теория четырёхполюсников позволяет производить анализ и синтез цепей различных как по структуре и сложности, так и по принципу работы, не рассчитывая токи и напряжения всех реальных элементов внутри четырёхполюсников, что весьма упрощает и ускоряет получение результата. Например, сложную электрическую цепь можно представить в виде совокупности соединённых друг с другом исходных четырёхполюсников. Теория позволяет найти параметры эквивалентного обобщающего четырёхполюсника и рассчитать его входные и выходные сопротивления по известным параметрам исходного четырёхполюсника.

Различают линейные и нелинейные четырёхполюсники.

Четырёхполюсник называют линейным, если в его состав входят элементы только с линейными вольтамперными характеристиками. Четырёхполюсник называют нелинейным, если он содержит хотя бы один нелинейный элемент.

По наличию или отсутствию внутренних источников энергии четырёхполюсники делят на активные (автономные и неавтономные) и пассивные.

Активными автономныминазывают четырёхполюсники, содержащие независимые некомпенсированные источники эдс или тока. Независимыми называют источники, которые создают в ветвях четырёхполюсника токи и напряжения при отсутствии внешнего сигнала. Источник называют некомпенсированным, если между выводами четырёхполюсника существуют напряжения при отсутствии внешних цепей.

Активными неавтономными называют четырёхполюсники, содержащие зависимые источники эдс или тока как в сочетании с независимыми компенсированными источниками, так и без них. Генераторы эдс и тока, действие которых проявляется только при наличии внешних источников сигнала, называют зависимыми или неавтономными. К активным неавтономным относят, например, четырёхполюсники, содержащие транзисторы.

Четырёхполюсники называют пассивными, если они не содержат источников электрической энергии или являются линейными и содержат независимые компенсированные источники. При отсутствии внешних сигналов у пассивных четырёхполюсников напряжения между двумя любыми выводами равны нулю.

Четырёхполюсники делят на обратимые и необратимые.

Четырёхполюсник называют обратимымили взаимным, если для него выполняется принцип взаимности: отношение напряжения на входе к току на выходе не зависит от того, какая из двух пар выводов является входной и какая выходной.

Четырёхполюсники могут быть симметричными и несимметричными.

Четырёхполюсник называют симметричным, если перемена местами его входных и выходных зажимов не изменяет токов и напряжений во внешних цепях. Симметричные четырёхполюсники всегда обратимы. Электрическая симметрия не требует геометрической (топологической) симметрии его схемы. Однако если обратимый четырёхполюсник имеет топологическую симметрию, то одновременно обязательно существует электрическая симметрия.

Пассивные линейные четырёхполюсники всегда являются обратимыми.

Активные четырёхполюсники могут быть как обратимыми, так и необратимыми, причём активные несимметричные четырёхполюсники являются необратимыми.

Характеристики четырёхполюсника полностью описываются входными и выходными токами и напряжениями. Выбирая две любые из этих величин в качестве независимых, две оставшиеся можно выразить через них в виде системы из двух линейных алгебраических уравнений. Систему уравнений четырёхполюсника можно записать в виде одной из шести форм, что определяется выбранным сочетанием независимых величин.

1. Форма Y-параметров или, более кратко, форма .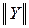

Здесь независимыми считают напряжения 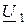и , а зависимыми – токи и :

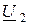
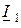
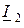
или в матричной записи

2. Форма Z-параметров или :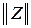

3. Форма A-параметров или :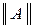

4. Форма H-параметров или :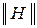

Если в качестве независимых выбраны 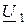и , то система уравнений будет записана в параметрах, если независимыми являются и , то – в параметрах.

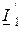
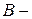
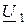
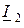
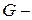
Коэффициенты уравнений четырёхполюсника являются его первичными параметрами.

Выбор системы уравнений определяется в основном удобством экспериментального нахождения параметров. А именно, в качестве независимых токов и напряжений принимают те, которые для данного четырёхполюсника наиболее удобно изменять в процессе измерений, что однозначно определяет тип параметров и форму системы уравнений.

Чаще других применяют 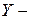, , и параметры. Например, свойства транзисторов в справочниках описывают через параметры, так как наиболее удобно изменять ток базы и напряжение между коллектором и эмиттером .

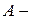
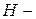
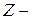
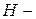
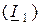
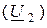
Коэффициенты одной системы уравнений могут быть выражены через коэффициенты любой другой.

Пусть, например, известны 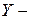параметры четырёхполюсника, а требуется найти его параметры.

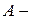
Для решения задачи преобразуем второе уравнение системы (19.1) к виду (19.4)

Подставим это уравнение в первое выражение из (19.1) и после преобразования получим

Сравнивая уравнения (19.6) и (19.7) с системой уравнений (19.4) и учитывая, что 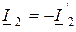, получаем

где

Поэтому достаточно знать параметры четырёхполюсника в какой-либо одной форме записи, чтобы получить их в любой другой. В литературе [1] и [3] имеются таблицы, облегчающие переход от одного вида параметров к другому.

Источник

po_temam / Четырехполюсники

Общая теория четырехполюсников.

Четырехполюсником называют часть электрической цепи, имеющей две пары зажимов, которые могут быть входными или выходными. К входным зажимам присоединяют источник питания, а к выходным зажимам – приемники энергии.

Теория четырехполюсников дает возможность единым методом анализировать электрические схемы большого объема.

Пассивный четырехполюсник – не содержащий источников энергии (ЛЭП, усилители).

Активный четырехполюсник – содержащий источники энергии.

Автономный четырехполюсник – у которого действие внутренних независимых источников энергии не компенсируется.

Линейные и нелинейные четырехполюсники.

Четырехполюсник является нелинейным, если в четырехполюснике имеется хотя бы один нелинейный элемент.

Симметричный и несимметричный четырехполюсник.

Симметричный четырехполюсник – это четырехполюсник, в котором перемена местами его входных и выходных зажимов не изменяет его входных и выходных токов и напряжений.

Уравнение линейного, пассивного четырехполюсника.

или в матричной форме

=А,

где и — матрицы-столбцы напряжения и тока на первичных и вторичных выводах соответственно

А=— квадратная матрица коэффициентов.

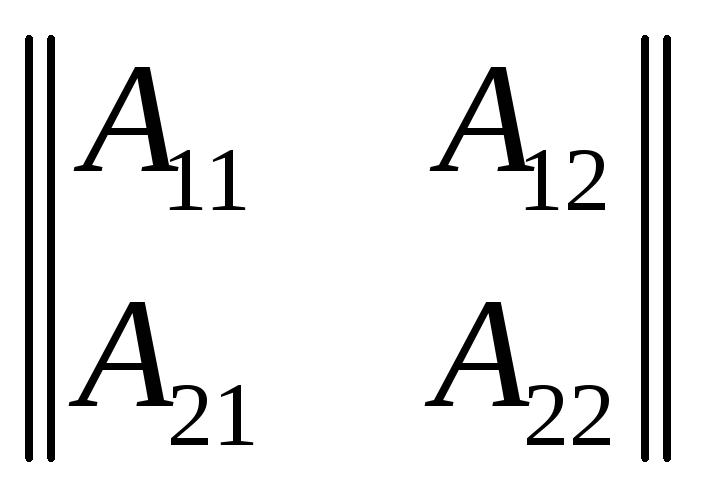
Всего можно записать 6 различных по форме, но по существу эквивалентных пар уравнений.

Y = или

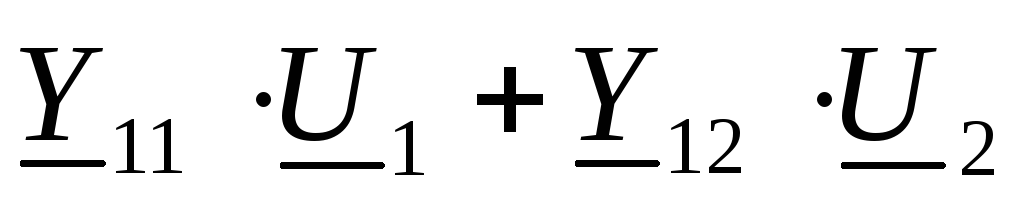
Z или

H или

G или

B или

Эквивалентные четырехполюсники – четырехполюсники у которых при взаимной замене входные и выходные токи и напряжения не изменяются.

Линейный, пассивный четырехполюсник в установившемся синусоидальном режиме.

∆₁₁/∆; ∆=; ∆₁₁=;

∆₁₁/∆-∆₁₂/∆; =∆₂₁/∆-∆₂₂/∆;

;

; Z₁₂=-Z₂₁;Y₁₂=-Y₂₁ ;

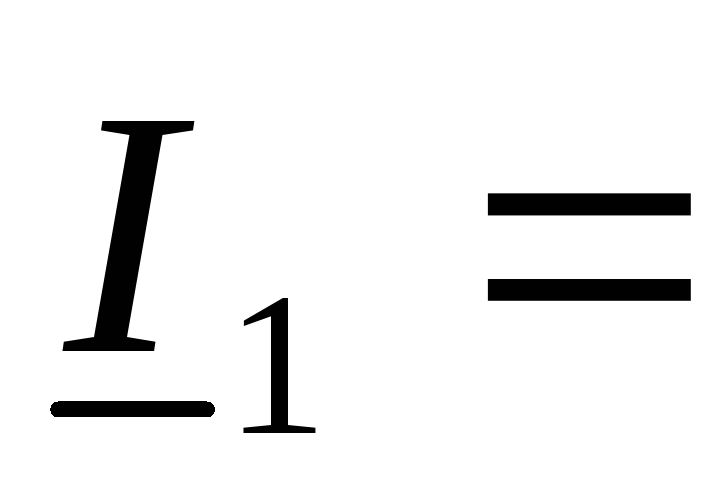
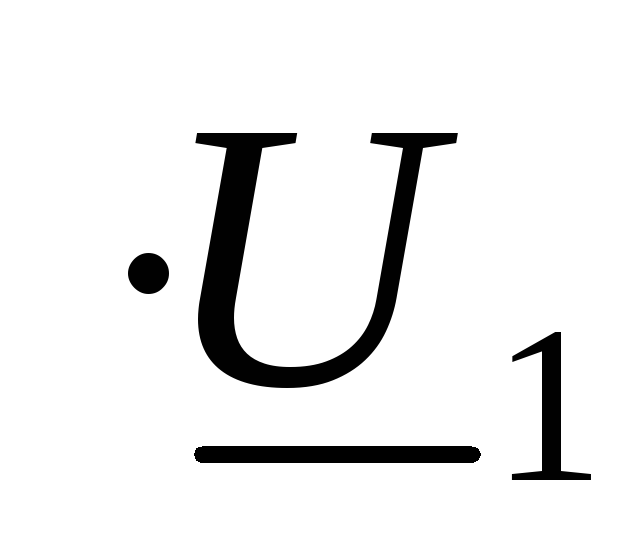
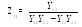
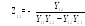
Перейдем к системе А параметров

Подставляем полученный результат в (*):

Используя выражения (1) и (2) запишем систему:

,где

Таким образом, пассивный четырехполюсник характеризуется тремя независимыми параметрами, а четвертый определяется из этих независимых.

Экспериментальное определение параметров четырехполюсников.

Измерение параметров при Z_пр=∞ I₂=0 – опыт холостого хода(ХХ)

Измерение параметров при Z_пр=0 U₂=0 – опыт короткого замыкания(КЗ)

Особо важно при измерении параметров мощных устройств, так как мощность в опытах ХХ и КЗ меньше, чем в номинальном режиме.

Тогда для опыта холостого хода имеем:

И для опыта короткого замыкания:

Из полученных выражений можно найти :

Эквивалентные схемы четырехполюсников.

Источник

Уравнения четырехполюсника с А – параметрами

ЧЕТЫРЕХПОЛЮСНИКИ

Общие положения

Четырехполюсником называют электрическую схему, имеющую два входных и два выходных зажима (полюса). Трансформатор, электрический фильтр, усилитель, линию электропередачи, линию связи и другие устройства можно рассматривать как четырехполюсник, который является промежуточным звеном меду источником и приемником электрической энергии.

Четырехполюсник принято изображать в виде прямоугольника с входными (1-1′) и выходными (2-2′) зажимами (рис.1.1).

Рис. 1.1. Направления напряжений и токов при прямой и обратной передаче

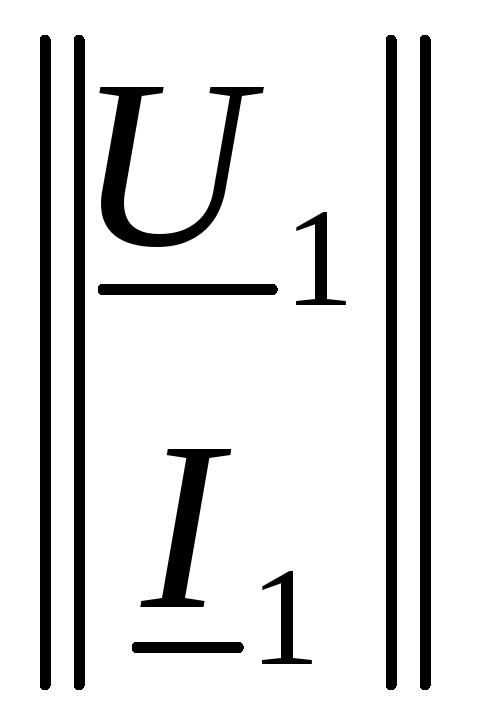
К входным зажимам подключается источник электрической энергии, к выходным – нагрузка. Напряжение и ток на входе обозначают 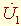, , на выходе , .

Принятые на рис. 1.1 положительные направления токов , соответствуют прямойпередаче энергии (от входных зажимов к выходным), направления токов , – обратной передаче, когда источник подключен к зажимам (2-2′), а нагрузка к зажимам (1-1′).

Понятием «четырехполюсник» пользуются тогда, когда интересуются токами и напряжениями только на его входных и выходных зажимах.

Четырехполюсники делятся на активные и пассивные, линейные и нелинейные, симметричные и несимметричные.

Активные четырехполюсники содержат внутри источники электрической энергии. Если эти источники независимые, то на одной или обеих парах его разомкнутых зажимах появляется напряжение.

Четырехполюсник называется пассивным, если он не содержит источников электрической энергии, или же имеющиеся внутри схемы источники компенсируют друг друга так, что на разомкнутых зажимах напряжения отсутствуют.

Линейные и нелинейные четырехполюсники содержат соответственно линейные и нелинейные элементы.

Симметричные четырехполюсники имеют одинаковые параметры со стороны входных и выходных зажимов.

Сложная электрическая цепь, например, канал передачи сигнала, представляет собой совокупность четырехполюсников, соединенных по определенной схеме.

Системы уравнений пассивных четырехполюсников

Уравнения четырехполюсника устанавливают связь между токами и напряжениями на его зажимах. Возможны шесть форм записи основных уравнений четырехполюсника:

1. Форма [А], где [А] – матрица коэффициентов, входящих в уравнения:

Уравнения (1.1) соответствуют выбору направления токов прямой передачи (рис. 1.1).

2. Форма [В]:

Уравнения (1.2) соответствуют выбору направления токов обратной передачи (рис. 1.2), что равносильно замене входных зажимов входными.

Остальные четыре формы уравнений четырехполюсника используют положительные направления токов прямой и обратной передач сигнала:

3. Форма [Y]:

4. Форма [Z]:

5. Форма [H]:

6. Форма [F]:

Коэффициенты уравнений в общем случае комплексные величины и зависят от частоты. Из четырех коэффициентов каждой системы уравнений (1.1) – (1.6) только три независимые, при этом выполняются соотношения:

Коэффициенты уравнений четырехполюсника называются соответственно А, В, Y, Z, H, F – параметрами четырехполюсника. Они определяются только схемой самого четырехполюсника и имеют физический смысл входной или передаточной функции.

В симметричном четырехполюснике кроме соотношений (1.7) имеют место равенства:

Поэтому симметричный четырехполюсник характеризуется лишь двумя независимыми параметрами.

Из перечисленных выше шести форм уравнений рассмотрим более подробно форму [А].

Уравнения четырехполюсника с А – параметрами

В курсе ТОЭ часто коэффициенты матрицы [А] обозначаются буквами А, В, С, D и уравнения записывают в виде:

где коэффициенты А и D – безразмерные, коэффициенты В имеет размерность сопротивления (Ом), а коэффициент С – размерность проводимости (См). Эти коэффициенты представляют собой:

– отношение напряжений при разомкнутых выходных зажимах;