отношение длины к окружности к длине диаметра
Длина окружности
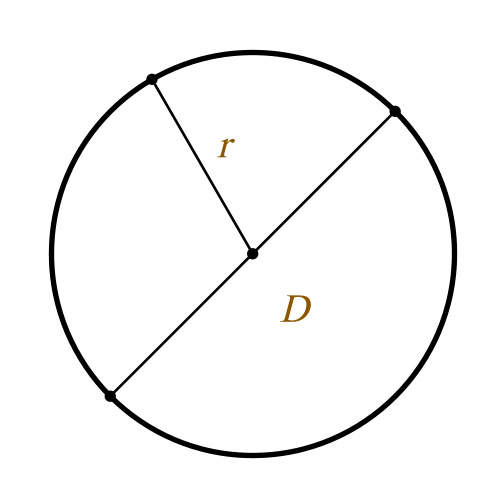
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
r – радиус окружности
D – диаметр окружности
L – длина окружности
Пример нахождения длинны окружности
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Формула для вычисления дины окружности имеет вид:
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Отношение длины окружности к диаметру
Рассматривая процесс нахождения длины окружности, можно заметить, что число, на которое нужно умножить диаметр, чтобы получить длину окружности, не зависит от величины самого диаметра, так что если мы нашли, что длина какой-нибудь окружности равна её диаметру, умноженному на некоторое число, то и длина всякой другой окружности будет равна её диаметру, умноженному на то же самое число.
Обозначим через Рn переменный периметр правильного многоугольника, вписанного в первую окружность, и через рn переменный периметр правильного многоугольника с тем же числом сторон, вписанного во вторую окружность.
На основании формулы Pn = 2Rn • sin 180° /n, мы можем написать:
Переменный периметр Рn имеет пределом длину С первой окружности. Переменный периметр рn имеет пределом длину c второй окружности. А потому из равенства \(\frac
Таким образом, мы можем сказать, что отношение длины окружности к её диаметру есть число постоянное для всех окружностей.
Это постоянное число принято обозначать греческой буквой π. Обозначение это введено, по всей вероятности, в XVII столетии. Буква π (пи) есть начальная буква греческого слова περιφερεια (окружность).
Мы можем, таким образом, для длины С окружности написать такую формулу:
С = 2R • π, или С = 2πR.
Доказано, что число π является числом иррациональным, и, значит, оно не может быть выражено точно никаким рациональным числом. Но его приближённые значения можно находить различными способами с какой угодно точностью. Приняв периметр вписанного 96-угольника за приближённую длину окружности, мы получим для π приближённое значение 3,14 с недостатком и с точностью до 0, 01. Эта точность для практических целей часто бывает достаточна. Для более точных вычислений можно брать
При решении геометрических задач часто встречается число, обратное числу π, т. е. равное дроби 1 /π. Полезно запомнить несколько цифр этого числа:
Длина дуги, содержащей n градусов.
Длина окружности есть 2πR, значит, длина дуги в 1° равна 2πR /360 = πR /180; следовательно, длина s дуги, содержащей n°, выразится так:
Если дуга выражена в минутах (’) или в секундах («), то длина её определяется соответственно формулами:
Задача. Вычислить с точностью до 1 мм радиус такой окружности, дуга которой, содержащая 81°21’ 36″, равна 0,452 м.
Обратив 81°21’ 36″ в секунды, получим число 292 896. Из уравнения
R = 0,452•180•60•60 /292896π = 1 /π = 0,318 (м)
Задача. Определить число градусов дуги, длина которой равна радиусу.
Заменив в формуле, определяющей длину дуги в n°, величину s на R, получим уравнение:
n° = 180° /π = 180° • 1 /π = 180° • 0,3183098 = 57°295764 = 57°17’ 44″,8.
Заметим, что дуга, равная радиусу, называется радианом.
1(радиан) \(\approx\) 57°17’ 45″
Радианы специального обозначения не имеют. Угол равный α радианов обозначается просто α.
Переход от одного измерения к другому производится по формулам:
Длина окружности
Возьмем циркуль. Установим ножку циркуля с иглой в точку « O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Диаметр окружности обозначается буквой « D ». На рисунке выше — это отрезок « BC ».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение « D = 2R ».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
π ≈ 3,14…
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2 π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Определите диаметр окружности, если её длина равна 56,52 дм. ( π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки « A » и « B ». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга « AB » и черная дуга « AB ». Точки « A » и « B » называют концами дуг.
Соединим точки « A » и « B » отрезком. Полученный отрезок называют хордой.
Точки « A » и « B » делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга « AB ».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.
Как найти диаметр окружности
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как апельсин 🍊 и тарелка.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Записывайтесь на курсы по математике для учеников с 1 по 11 классы.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
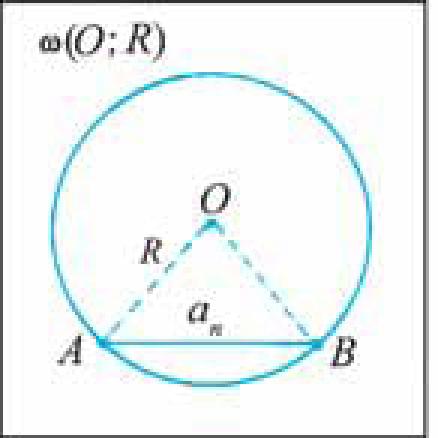
2. Теорема об отношении длины окружности к ее диаметру.
Докажем теорему, которая характеризует отношение длины окружности к ее диаметру.
Скачено с Образовательного портала www.adu.by
Глава 3
Дано: со (О; 7?), ю! (0[; 7?!) — окружности, С, С1 — длины окружностей. Доказать: С С[ 2R 2R
Скачено с Образовательного портала www.adu.by
Теперь воспользуемся формулой, по которой находится сторона правильного п-угольника через радиус описанной окружности. Учитывая эту формулу (§ 1, п. 4, гл. 3), можем записать равенства
3) Это равенство верно при любом значении п. Будем неограниченно увеличивать число п, тогда периметр Рп первого многоугольника стремится к длине С первой окружности, а периметр Р‘п второго
многоугольника стремится к длине Сх другой окружности, т. е.
Отсюда следует, что
Значит, отношение длины окружности к ее диаметру одно и то же для всех окружностей.
Число, равное отношению длины окружности к ее диаметру, обозначается строчной греческой буквой % (читается «пи»). Доказано, что число п — иррациональное, т. е. выражается бесконечной непериодической десятичной дробью. Приближенное значение числа п с точностью до восьми знаков после запятой такое:
% & 3,14159265. При решении задач в школьной практике пользуются приближенным значением числа п с точностью до сотых: п » 3,14.
формулы длины окружности воспользуемся равенством
Теперь выведем формулу для вычисления длины / дуги, градусная мера которой равна а. Пусть данная дуга является дугой окружности радиуса R. Так как длина всей окружности равна 2%R, то длина дуги в
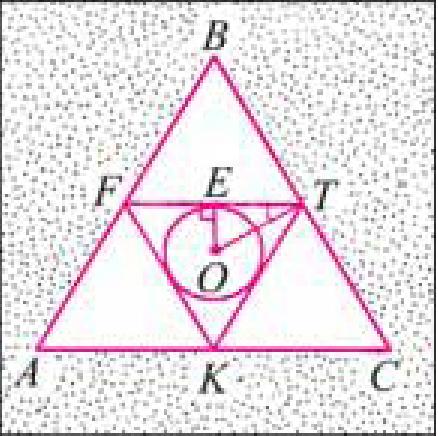
Задача 1. Точки F, ТиК — середины сторон равностороннего треугольника ABC. Найдите длину окружности, вписанной в треугольник FTK, если сторона треугольника ABC равна а.