отношение делимости на множестве целых чисел и его свойства

Отношение делимости и его свойства

Пусть даны натуральные числа a и b. Говорят, что число a делится на число b, если существует такое натуральное число q, что a = bq.

В этом случае число b называют делителем числа а, а число а – кратным числа b.

Например, 24 делится на 8, так как существует такое q = 3, что 24 = 8*3. Можно сказать иначе: 8 – это делитель числа 24, а 24 есть кратное числа 8.

В случае, когда а делится на b, пишут: . Эту запись часто читают и так: «а кратно b».

Заметим, что понятие «делитель данного число» следует отличать от понятия «делитель», обозначающего то число, на которое делят. Например, если 18 делят на 5, то число 5 – делитель, но 5 не является делителем числа 18. Если 18 делят на 6, то в случае понятия «делитель» и «делитель данного числа» совпадают.

Из определения отношения делимости и равенства а = 1*а, справедливого для любого натурального а, вытекает, 1 является делителем любого натурального числа.

Выясним, сколько вообще делителем может быть у натурального числа. Сначала рассмотрим следующую теорему.

Теорема. Делитель b данного числа а не превышает этого числа. Если , то .

Доказательство. Так как , то существует такое , что a = bq, значит, a – b = bq – b = b*(q – 1). Поскольку , то . Тогда и, следовательно, .

Из данной теоремы следует, что множество делителей данного числа конечно. Назовем, например, все делители числа 36. Они образуют конечное множество <1, 2, 3, 4, 6, 9, 12, 18, 36>.

Свойства делимости

Нам известно, что отношение делимости на множестве N обладает рядом свойств, в частности, оно рефлексивно, антисимметрично и транзитивно. Теперь, имея определение отношения делимости, мы можем доказать эти и другие его свойства.

Теорема. Отношение делимости рефлексивно, т.е. любое нату­ральное число делится само на себя.

Доказательство. Для любого натурального а справедливо ра­венство . Так как 1 е N, то, по определению отношения дели­мости, .

Теорема. Отношение делимости антисимметрично, т.е. если и , то .

Доказательство. Предположим противное, т. е. что . Но тог­да , согласно теореме, рассмотренной выше.

По условию и . Тогда, по той же теореме,.

Неравенства и будут справедливы лишь тогда, когда , что противоречит условию теоремы. Следовательно, наше предпо­ложение неверное и теорема доказана.

Теорема. Отношение делимости транзитивно, т.е. если и , то .

Доказательство. Так как, то существует такое натуральное число q, что а = bq, а так как , то существует такое натуральное число p, что . Но тогда имеем: . Число pq – натуральное. Значит, по определению отношения делимости,.

Например, не производя вычислений, можно сказать, что сумма 175 + 360 + 915 делится на 5, так как на 5 делится каждое слагаемое этой суммы.

Теорема (признак делимости разности). Если числа а1 и а2 делятся на b и , то их разность делится на b.

Доказательство этой теоремы аналогично доказательству призна­ка делимости суммы.

Теорема (признак делимости произведения). Если число а де­лится на b, то произведение вида ах, где xÎ N, делится на b.

Доказательство. Так как , то существует такое натураль­ное число q, что . Умножим обе части этого равенства на нату­ральное число х. Тогда ах = (bq)x, откуда на основании свойства ассоциативности умножения (bq)x = b(qx) и, значит, ах = b(qx), где qx – натуральное число. Согласно определению отношения делимости, , что и требовалось доказать.

Из доказанной теоремы следует, что если один из множителей произведения делится на натуральное число b, то и все произведение делится на b.

Источник

Отношение делимости и его свойства

Делимость натуральных чисел

Нам известно, что отношение делимости обладает рядом свойств, в частности, оно рефлексивно, антисимметрично и транзитивно. Теперь, имея определение отношения делимости, мы можем доказать эти и другие его свойства.

Теорема2. Отношение делимости рефлексивно, т.е. любое натуральное число делится само на себя.

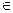
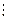
Доказательство. Для любого натурального а справедливо равенство а = а·1. Так как 1 N, то, по определению отношения делимости, а а.

Теорема 3. Отношение делимости антисимметрично, т.е.

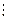
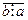
если a b и а≠b, то .

Доказательство. Предположим противное, т.е. что b 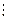а. Но тогда а ≤ b, согласно теореме, рассмотренной выше.

По условию a 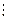b и а≠b. Тогда, по той же теореме, b≤а.

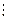
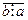
Неравенства а ≤b и b ≤а будут справедливы лишь тогда, когда а=b, что противоречит условию теоремы. Следовательно, наше предположение неверное и поэтому если a b и а≠b, то .

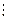
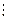
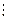
Теорема 4. Отношение делимости транзитивно, т.е. если a b и b с, то а с.

Например, не производя вычислений, можно сказать, что сумма 175 + 360 + 915 делится на 5, так как на 5 делится каждое слагаемое этой суммы.

Доказательство этой теоремы аналогично доказательству признака делимости суммы.

Теорема 7 (признак делимости произведения). Если число а делится на b, то произведение вида ах, где х 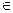N, делится на b.

Из доказанной теоремы следует, что если один из множителей произведения делится на натуральное число b, то и все произведение делится на b.

Рассмотрим еще три теоремы, связанные с делимостью суммы и произведения, которые часто используются при решении задач на делимость.

Теорема 8. Если в сумме одно слагаемое не делится на число b, а все остальные слагаемые делятся на число b, то вся сумма на число b не делится.

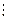
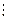
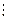
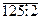
Например, сумма 34 + 125 + 376 + 1024 на 2 не делится, так как 34 2, 376 2,124 2, но .

Теорема 9. Если в произведении ab множитель а делится на натуральное число m, а множитель b делится на натуральное число n, то ab делится на mn.

Справедливость этого утверждения вытекает из теоремы о делимости произведения.

Доказательство. Так как ас делится на bс, то существует такое натуральное число q, что ас = (bc)q, откуда ас = (bq)c и, следовательно, а =bq, т.е. а 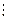b.

Признаки делимости

Рассмотренные в п. 88 свойства отношения делимости позволяют доказать известные признаки делимости чисел, записанных в десятичной системе счисления, на 2, 3,4, 5, 9.

Признаки делимости позволяют установить по записи числа делится ли оно на другое, не выполняя деления.

Теорема 11 (признак делимости на 2). Для того чтобы число х делилось на 2, необходимо и достаточно, чтобы его десятичная запись оканчивалась одной из цифр 0, 2, 4, 6, 8.

Докажем обратное: если число х делится на 2, то его десятичная запись оканчивается одной из цифр 0, 2,4, 6, 8.

Теорема 12 (признак делимости на 5). Для того чтобы число х делилось на 5, необходимо и достаточно, чтобы его десятичная запись оканчивалась цифрой 0 или 5.

Доказательство этого признака аналогично доказательству признака делимости на 2.

Теорема 13 (признак делимости на 4). Для того чтобы число х делилось на 4, необходимо и достаточно, чтобы на 4 делилось двузначное число, образованное последними двумя цифрами десятичной записи числа х.

Докажем обратное, т.е. если число х делится на 4, то двузначное число, образованное последними цифрами его десятичной записи, тоже делится на 4.

Например, число 157872 делится на 4, так как последние две цифры в его записи образуют число 72, которое делится на 4. Число 987641 не делится на 4, так как последние две цифры в его записи образуют число 41, которое не делится на 4.

Теорема 14 (признак делимости на 9). Для того чтобы число х делилось на 9, необходимо и достаточно, чтобы сумма цифр его десятичной записи делилось на 9.

В последней сумме каждое слагаемое делится на 9:

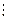
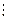
а₁·(10-1) 9, так как (10-1) 9,

Следовательно, х 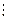9.

Докажем обратное, т.е. если х 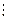9, то сумма цифр его десятичной записи делится на 9.

Например, число 34578 делится на 9, так как сумма его цифр, равная 27, делится на 9. Число 130542 не делится 9, так как сумма его цифр, равная 15, не делится на 9.

Теорема 15 (признак делимости на 3). Для того чтобы число х делилось на 3, необходимо и достаточно, чтобы сумма цифр его десятичной записи делилось на 3.

Доказательство этого утверждения аналогично доказательству признака делимости на 9.

Источник

Определение отношения делимости на множестве целых неотрицательных чисел. Свойства отношения делимости. Делимость суммы, разности, произведения целых неотрицательных чисел

Пусть даны натуральные числа а и b. Говорят, что а делится на число b, если существует такое натуральное число q, что а = bq. b – делитель числа а; а – кратное числа b.

1 – делитель любого натурального числа

Делитель b данного числа а не превышает этого числа.

Простым числом называется такое натуральное число, больше 1, которое имеет только два делителя – единицу и само это число.

Составным числом называется такое натуральное число, которое имеет более двух делителей.

Число 1 не является ни простым, ни составным числом в связи с тем, что оно имеет только 1 делитель.

тельное число, то равенство а = с*р означает, что а:с. Теорема доказана.

Признак делимости суммы. Если каждое слагаемое делится на натуральное число n, то и их сумма делится на это число.

Признак делимости разности. Если числа а и b делятся на n и а ≥ b, то а – b делится на n.

Признак делимости произведения. Если один из множителей произведения делится на натуральное число n, то и все произведение делится на n.

Признаки делимости на 2, 5, 10.

Признак делимости на 2. Для того чтобы число х делилось на 2, необходимо и достаточно чтобы его десятичная запись оканчивалась одной из цифр 0, 2, 4, 6, 8.

Признак делимости на 5. Для того чтобы число х делилось на 5, необходимо и достаточно, чтобы его десятичная запись оканчивалась цифрой 0 или 5.

Признак делимости на 10. Для того чтобы число х делилось на 10, необходимо и достаточно, чтобы его десятичная запись оканчивалась цифрой 0.

Дата добавления: 2015-04-18 ; просмотров: 163 ; Нарушение авторских прав

Источник

Отношение делимости и его свойства

Лекция 44. Делимость целых неотрицательных чисел

ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ

1. Отношение делимости на множестве неотрицательных чисел.

2. Свойства отношения делимости.

3. Делимость суммы, разности и произведения целых неотрицательных чисел.

Из определения отношения делимости и равенства а = 1·а, справедливого для любого натурального а, вытекает, что 1 является делителем любого натурального числа.

Выясним, сколько вообще делителей может быть у натурального числа а. Сначала рассмотрим следующую теорему.

Теорема1. Делитель b данного числа а не превышает этого числа, т.е. если

Из данной теоремы следует, что множество делителей данного числа конечно. Назовем, например, все делители числа 36. образуют конечное множество <1,2,3,4,6,9,12,18,36>.

В зависимости от числа делителей среди натуральных чисел различают простые и составные числа.

Например, число 13- простое, поскольку, у него только два делителя: 1 и 13.

Определение. Составным числом называется такое нату­ральное число, которое имеет более двух делителей.

Так число 4 составное, у него три делителя: 1,2 и 4.

Число 1 не является ни простым, ни составным числом в связи с тем, что оно имеет только один делитель.

Нам известно, что отношение делимости обладает рядом свойств, в частности, оно рефлексивно, антисимметрично и транзитивно. Теперь, имея определение отношения делимо­сти, мы можем доказать эти и другие его свойства.

Теорема 2. Отношение делимости рефлексивно, т.е. любое натуральное число делится само на себя.

Доказательство. Для любого натурального а справед­ливо равенство а = а·1. Так как 1 Є N, то, по определению отношения делимости, а : _. а.

то b ⁞͞ a.

Доказательство. Предположим противное, т.е. что b⁞a. Но тогда а ≤ b, согласно теореме, рассмотренной выше.

По условию и а ⁞. b и а ≠ b. Тогда, по той же теореме, b ≤ а.

Неравенства а ≤ b и b ≤ а будут справедливы лишь тогда, когда а = b, что противоречит условию теоремы. Следова­тельно, наше предположение неверное и теорема доказана.

Теорема 4. Отношение делимости транзитивно, т.е. если а⁞ b и b⁞ с, то а⁞ с.

а⁞ с.

Например, не производя вычислений, можно сказать, что 175 + 360 + 915 делится на 5, так как на 5 делится каждое слагаемое этой суммы.

Доказательство этой теоремы аналогично доказательству признака делимости суммы.

Теорема 7 (признак делимости произведения). Если число а делится на b, то произведениe вида ах, где х Є N, делитcя на b.

Из доказанной теоремы следует, что если один из множителей произведения делится на натуральное число b, то и все произведение делится на b. Например, произведение 24·976·305 делится на 12, так как на 12 делится множитель 24.

Рассмотрим еще три теоремы, связанные с делимостью суммы и произведения, которые часто используются при решении задач на делимость.

Теорема 8. Если в сумме одно слагаемое не делится на число b, а все остальные слагаемые делятся на число b, то вся cумма на число b не делится.

Теорема 9. Если в произведении ab множитель a делится на натуральное число т, а множитель b делится на натуральное число n,то ab делится на mn.

Справедливость этого утверждения вытекает из теоремы о делимости произведения.

1.Объясните, почему число 15 является делителем числа 60 и не является делителем числа 70.

2.Постройте граф отношения «быть делителем данного числа», заданного на множестве Х = <2, 6,. 12, 18, 24>. Как от­ражены на этом графе свойства данного отношения?

4. Запишите множество делителей числа.

5.На множестве X = <1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11; 12>задано отношение «иметь одно и то же число делителей». Является ли оно отношением эквивалентности?

6.Постройте умозаключение, доказывающее, что:

а) число 19 является простым;

б) число 22 является составным.

7.Докажите или опровергните следующие утверждения:

а) Если сумма двух слагаемых делится на некоторое число, то и каждое слагаемое делится на это число.

б) Если одно из слагаемых суммы не делится на некоторое число, то и сумма не делится на это число.

в) Если ни одно слагаемое не делится на некоторое число, то и сумма не делится на это число.

г) Если одно из слагаемых суммы делится на некоторое число, а другое не делится на это число, то и сумма не делится на это число.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Делимость суммы, разности, произведения целых неотрицательных чисел

Лекция 4. Делимость на множестве целых неотрицательных чисел

1. Понятие отношения делимости, его свойства.

2. Признаки делимости суммы, разности, произведения.

3. Признаки делимости на 2, 3, 4, 5, 9 (два доказать).

В начальном курсе математики делимость натуральных чисел, как правило, не изучается, но многие факты из этого раздела математики неявно используются.

Отношение делимости и его свойства

Рассмотрим отношение делимости на множестве целых неотрицательных чисел.

Обознаение: а b и говорят а кратно b, а b называют делителем числа а.

Замечание. Из определения 1 и равенства а=1а, следует, что 1 является делителем любого целого неотрицательного числа.

Свойства отношения делимости:

Отношение делимости рефлексивно, антисимметрично, транзитивно.

Теорема 1. Отношение делимости рефлексивно, т.е. любое натуральное число делится само на себя .

Для справедливо равенство а=а•1. Т.к. 1 , то по опр. 1 .

Теорема 2. Отношение делимости антисимметрично, т. е.

.

Доказательство (методом от противного): Предположим, что 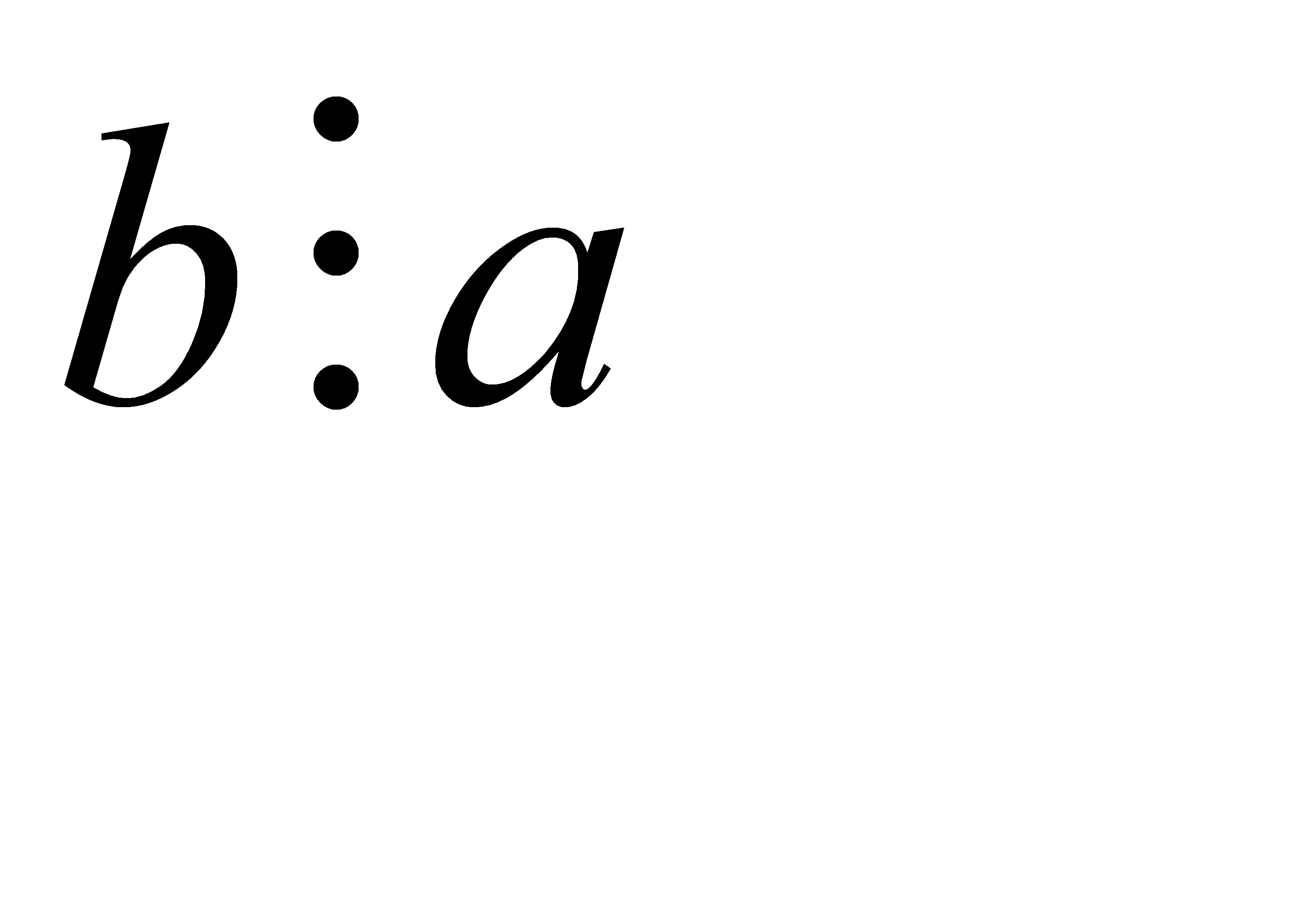. Тогда очевидно, что b≥a. Но по условию и значит а≥b. Выполнение этих неравенств возможно только при а=b, что противоречит условию. Следовательно, наше предположение неверно и справедливость свойства установлена.

Теорема 3. Отношение делимости транзитивно, то есть

.

Т.к. , то по опр.1 . Аналогично, т.к. b с, то .

Тогда a=bq=(cp)q=c(pq). Число рq- натуральное. Это означает по опр.1, что а с.

Таким образом, отношение делимости на множестве N, обладая свойствами рефлексивности, антисимметричности и транзитивности, является отношением нестрогого порядка.

Делимость суммы, разности, произведения целых неотрицательных чисел

Теорема 4 (признак делимости суммы):Если каждое слагаемое суммы делится на натуральное число b, то и вся сумма делится на это число, то есть

если .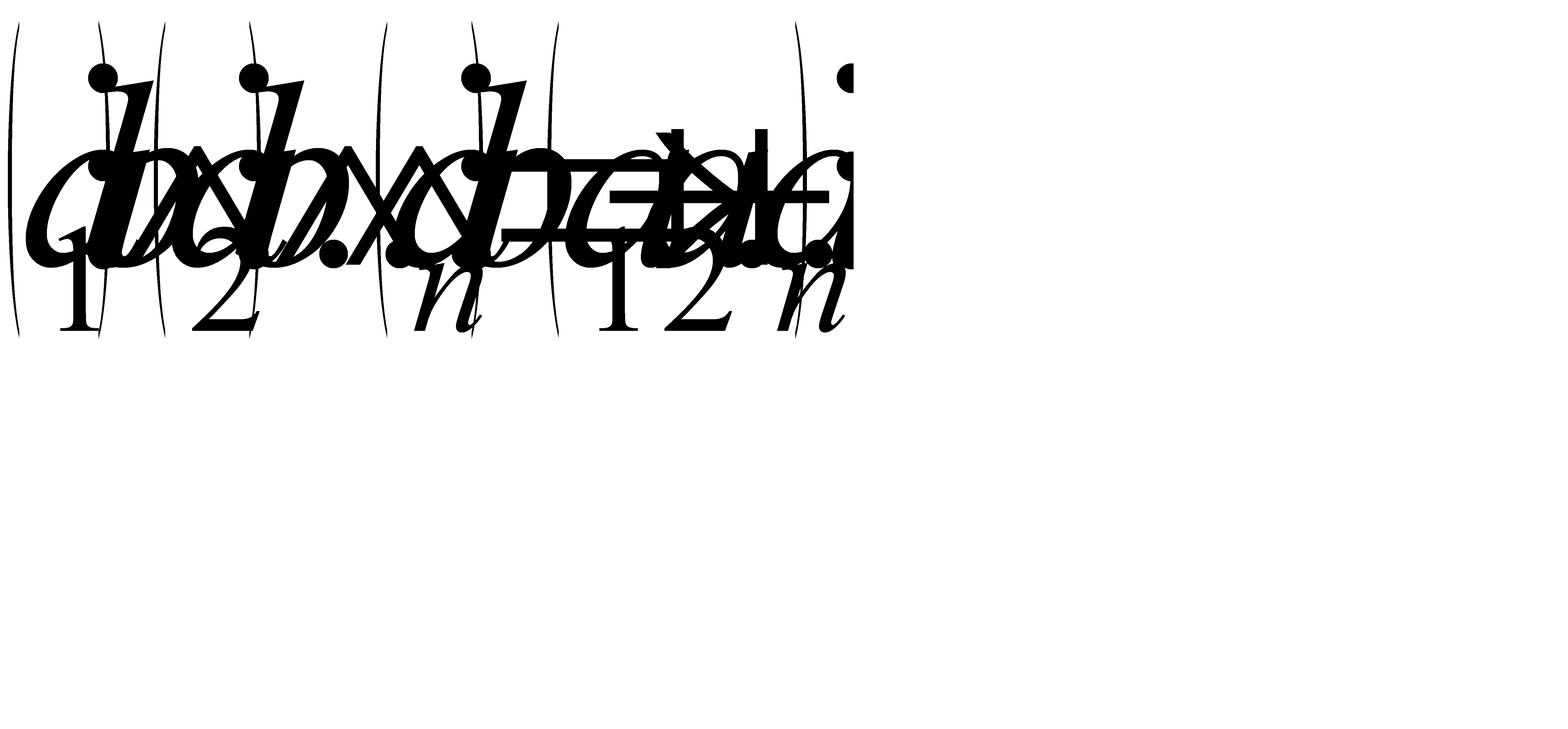

Доказательство: Пусть . Тогда существуют q₁,q₂,…q_n N такие, что выполняются равенства: а₁=bq₁, а₂=bq₂, …, а_1n=bq_n. Из этих равенств следует, что а₁+а₂+…а_n=bq₁+bq₂+…+bq_n=b(q₁+q₂+…+q_n), где q₁+q₂+…+q_n=q N₀. По определению отношения делимости это означает, что .

Теорема 5 (признак делимости разности): Если каждое из чисел а и b делится на с и а≥b, то разность а-b делится на с, т. е. если .

Доказательство: Пусть . Тогда существуют q₁,q₂ N такие, что а=cq₁, b=cq₂. Поскольку а≥b, то q₁>q₂. Таким образом, имеем а-b=cq₁-cq₂=c(q₁-q₂)=cq, где q₁-q₂=q N. Следовательно, .

Теорема 6 (признак делимости произведения): Если хотя бы один из множителей произведения делится на натуральное число b, то и все произведение делится на это число, то есть .

Доказательство: Пусть а_k b, тогда существует q N такое, что а_k=bq. Отсюда, используя коммутативный и ассоциативный законы умножения, можем записать . Поскольку произведение целых неотрицательных чисел является целым неотрицательным числом, то последнее равенство означает, что .

Теорема 7: Если в произведении ab множитель а делится на натуральное число m, а множитель b делится на натуральное число n, то произведение ab делится на произведение nm, то есть .

Доказательство: Пусть a m и b n, тогда существуют q₁,q₂ N такие что, a=mq₁, b=nq₂. Отсюда на основании комм. и ассоц. законов умножения имеем ab=(mq₁)(nq₂)=(mn)(q₁q₂)=(mn)q, где q₁q₂=q N_. следовательно, ab mn.

Теорема 8: Если в сумме одно слагаемое не делится на натуральное число b, а все остальные слагаемые делятся на это число, то и вся сумма на число b не делится.

Доказательство: Пусть S=a₁+a₂+…+a_n+c, где а₁ b, a₂ b, …, a_n b, но . Докажем, что . Предположим противное, то есть S b. Тогда с=S-(a₁+a₂+…+a_n), где S b, и (a₁+a₂+…+a_n) b. По теореме о делимости разности это означает, что с b. Полученное противоречие и доказывает теорему.

Признаки делимости

Теорема 9 (признак делимости на 2) Для того чтобы число х делилось на 2, необходимо и достаточно, чтобы его десятичная запись оканчивалась одной из цифр 0,2,4,6,8.

Доказательство. Пусть число х записано в десятичной системе счисления, т.е.

Докажем обратное: если число х делится на 2, то его десятичная запись оканчивается одной из цифр 0,2,4,6,8.

Теорема 10 (признак делимости на 5). Для того чтобы число х делилось на 5, необходимо и достаточно, чтобы его десятичная запись оканчивалась цифрой 0 или 5.

Доказательство этого признака аналогично доказательству признака делимости на 2.

Теорема 11 (признак делимости на 4). Для того чтобы число х делилось на 4, необходимо и достаточно, чтобы на 4 делилось двузначное число, образованное последними двумя цифрами десятичной записи числа х.

Доказательство. Пусть число х записано в десятичной системе счисления, т.е.

Докажем обратное, т.е. если число х делится на 4, тo двузначное число, образованное последними цифрами его десятичной записи, тоже делится на 4.

Теорема12 (признак делимости на 9)Для того чтобы число х делилось на 9, необходимо и достаточно, чтобы сум­ма цифр его десятичной записи делилось на 9.

В последней сумме каждое слагаемое делится на 9:

Теорема15 (признак делимости на 3):Для того чтобы число х делилось на 3, необходимо и достаточно, чтобы сум­ма цифр его десятичной записи делилась на 3.

Доказательство этого утверждения аналогично доказа­тельству признака делимости на 9.

Источник