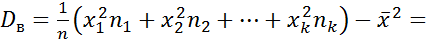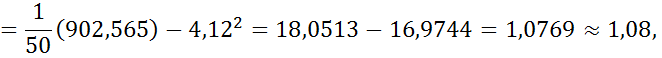отношение частоты варианты к объему выборки называется
Отношение частоты варианты к объему выборки называется
1. Задачи математической статистики.
4. Статистическое распределение выборки.
5. Эмпирическая функция распределения.
6. Полигон и гистограмма.
7. Числовые характеристики вариационного ряда.
8. Статистические оценки параметров распределения.
9. Интервальные оценки параметров распределения.
1. Задачи и методы математической статистики
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным- контролируемый размер детали.
Иногда проводят сплошное исследование, т.е. обследуют каждый объект относительно нужного признака. На практике сплошное обследование применяется редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов (выборочную совокупность) и подвергают их изучению.
Основная задача математической статистики заключается в исследовании всей совокупности по выборочным данным в зависимости от поставленной цели, т.е. изучение вероятностных свойств совокупности: закона распределения, числовых характеристик и т.д. для принятия управленческих решений в условиях неопределенности.
Генеральная совокупность – это совокупность объектов, из которой производится выборка.
Выборочная совокупность (выборка) – это совокупность случайно отобранных объектов.
Если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n = 100.
При составлении выборки можно поступить двумя способами: после того, как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки делятся на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Выборка должна правильно представлять пропорции генеральной совокупности. Выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществлять случайно.
Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается; в предельном случае, когда рассматривается бесконечная генеральная совокупность, а выборка имеет конечный объем, это различие исчезает.
В американском журнале «Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов относительно исхода предстоящих выборов президента США в 1936 году. Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве источника для генеральной совокупности исследуемых американцев были взяты справочники телефонных абонентов. Из них случайным образом были выбраны 4 миллиона адресов., по которым редакция журнала разослала открытки с просьбой высказать свое отношение к кандидатам на пост президента. Обработав результаты опроса, журнал опубликовал социологический прогноз о том, что на предстоящих выборах с большим перевесом победит Ландон. И … ошибся: победу одержал Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная часть населения, которые поддерживали взгляды Ландона.
На практике применяются различные способы отбора, которые можно разделить на 2 вида:
1. Отбор не требует расчленения генеральной совокупности на части (а) простой случайный бесповторный; б) простой случайный повторный).
2. Отбор, при котором генеральная совокупность разбивается на части. (а) типичный отбор; б) механический отбор; в) серийный отбор).
Простым случайным называют такой отбор, при котором объекты извлекаются по одному из всей генеральной совокупности (случайно).
Типичным называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типичной» части. Например, если деталь изготавливают на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда обследуемый признак заметно колеблется в различных «типичных» частях генеральной совокупности.
Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Например, если нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой отбор может не обеспечивать репрезентативность выборки (если отбирают каждый 20-ый обтачиваемый валик, причем сразу же после отбора производится замена резца, то отобранными окажутся все валики, обточенные затупленными резцами).
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергают сплошному обследованию. Например, если изделия изготавливаются большой группой станков-автоматов, то подвергают сплошному обследованию продукцию только нескольких станков.
На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы.
4. Статистическое распределение выборки
Если количество вариант велико или выборка производится из непрерывной генеральной совокупности, то вариационный ряд составляется не по отдельным точечным значениям, а по интервалам значений генеральной совокупности. Такой вариационный ряд называется интервальным. Длины интервалов при этом должны быть равны.
Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (суммы частот, попавших в этот интервал значений)
Точечный вариационный ряд частот может быть представлен таблицей:
Отношения частот к объему выборки
Тема. Элементы математической статистики
Введение
Понятие математической статистики.
Генеральная совокупность и выборка.
Вариационный и статистический ряды.
Интервальный статистический ряд.
Статистические характеристики выборки.
Вопрос 1. Понятие математической статистики
Слово «статистика» происходит от латинского слова «status» (состояние, государство) и означает определенное положение вещей.
Термин «статистика» впервые ввел немецкий ученый Г.Ахенвалль в 1749 г., в своей книге «О государствоведении».
Но непосредственно статистический учёт вёлся намного раньше:
— проводились переписи населения в Древнем Китае,
— осуществлялось сравнение военного потенциала государств,
— вёлся учёт имущества граждан в Древнем Риме, и др.
Для проведения «статистического учета» нужен был «фундамент», то есть математический аппарат и математическая методология. В результате возникла и развивалась наука «Математическая статистика».
Математическая статистика возникла в XVII в. и развивалась вместе с теорией вероятностей.
Основоположниками науки являются Я. Бернулли, К.Гаусс, П. Лаплас.
В XIX в. большой вклад внесли российские математики П.Чебышев, А. Марков, А. Ляпунов.
В XX в. важные результаты были получены советскими математиками В.И. Романовским, Е.Е. Слуцким, А.Н. Колмогоровым, Н.В. Смирновым, английскими учеными Э. Пирсоном, У.Го́ссе (Стьюдентом), Р. Фишером, Г. Крамером, американскими учеными Ю. Нейманом, А. Вальдом, Р. Мизесом и другими учеными.
Математическая статистика – раздел математики, разрабатывающий:
— методы регистрации данных произведенных наблюдений,
— методы описания данных произведенных наблюдений;
— методы анализа данных наблюдений и экспериментов – с целью построения вероятностно-статистических моделей случайных явлений.
Математическая статистика – это синтез Теории вероятности и Статистики.
Предметом математической статистики является изучение случайных величин (или случайных событий) по результатам наблюдений (статистическим данным).
Целью математической статистики является описание, объяснение и прогнозирование явлений действительности на основе проведенного анализа.
Задачей математической статистики является создание методов сбора и методов обработки статистических данных для получения научных и практических выводов.
Рассмотрим схему исследований при решении задач математической статистики.
Эти исследования делятся на два этапа:
1) На первом этапе, который называют описательной статистикой (descriptive statistics), когда путем наблюдений и экспериментов осуществляется:
— регистрация статистических данных,
— упорядочивание полученных данных,
— представление полученных данных в компактной, наглядной или функциональной форме,
— вычисление различных количественных параметров (показателей, например, средняя величина, мода, медиана, частота, частость и др.), характеризующих статистические данные.
2) На втором этапе на основе вычислений, проведенных на предшествующем этапе, предоставляются обоснованные выводы о свойствах исследуемого случайного явления, с помощью использования методов оценивания и проверки гипотез.
Современная математическая статистика разрабатывает способы определения числа необходимых наблюдений, испытаний до начала исследования (планирование эксперимента), а в ходе исследования (последовательный анализ) может принимать решения в условиях неопределенности.
Вопрос 2. Генеральная совокупность и выборка
Математическая статистика может исследовать любой абстрактный эксперимент, в результате проведения которого наблюдает или измеряет отдельные значения х изучаемой случайной величины Х:
это могут быть, например:
— параметры детали при массовом производстве,
— цена на жилье в отдельных районах или регионах,
— любой общий количественный признак определенного множества объектов.
Генеральной совокупностью называется множество возможных значений изучаемой случайной величины Х с законом распределения F ( X ).
Возможные значения генеральной совокупности Х называются ее элементами.
Закон распределения F ( X ) называется генеральным законом распределения.
Числовые характеристики Х называются генеральными числовыми характеристиками.
Генеральная совокупность может быть:
— конечной (множество значений случайной величины Х –конечно),
1) Х – число детей, родившихся в городе за определенный промежуток времени.
Генеральная совокупность в данном примере – конечное множество неотрицательных чисел <0,1,2,…>с некоторым законом распределения.
2) Х – величина отклонения детали от заданного размера при массовом производстве
Генеральная совокупность в данном примере – это бесконечное множество всех действительных чисел с некоторым законом распределения.
Иногда из всей генеральной совокупности случайно отбирают ограниченное число объектов и подвергают их изучению, по свойствам которой судят о свойствах генеральной совокупности.
В результате возникает понятие выборки:
Выборочной совокупностью или выборкой называется совокупность случайно отобранных элементов из генеральной совокупности.
Объемом выборки называется число ее элементов.
Выборку нельзя составить как попало.
Выборка должна быть репрезентативной (представительной) и однородной.
Репрезентативность обеспечивается простым случайным выбором:
1) Выбор является случайным.
2) Каждый элемент генеральной совокупности может быть выбран.
3) Каждый элемент выбирается независимо от остальных.
4) Все элементы попадают в выборку в результате равных условий попадания.
Однородность означает, что условия проведения экспериментов для получения выборки не должны меняться.
Но на практике простой случайный выбор не всегда осуществим (он является эталонным), а применяются различные виды выбора:
механический выбор (отбор) (измерения проводят через равные промежутки времени, контролируется каждая m деталь, выбирается каждый s человек по списку);
серийный выбор (отбор) (контролируется не одна таблетка, а вся упаковка, не один человек группы, а вся группа);
типический выбор (отбор) (урожайность участка, социологический опрос, зарплата в отрасли);
выбор с помощью случайных независимых измерений (температура среды, загрязненность воды, величина тока) и другие.
Все виды выборов (отборов) могут комбинироваться между собой.
В математической статистике применяется только простой случайный выбор.
После того как сделана выборка, все ее элементы обследуют по отношению к генеральной совокупности и в результате получают наблюдаемые данные. Далее они упорядочиваются, представляются в компактной, наглядной или функциональной форме. Вычисляются различные средние величины, характеризующие всю Генеральную совокупность в целом.
Вопрос 3. Вариационный и статистические ряды
Обычно выборка представляет собой множество чисел, расположенных в беспорядке.
Для дальнейшего изучения выборку подвергают обработке.
Наблюдаемые значения выборки называются вариантами.
Последовательность всех вариант, записанных в возрастающем порядке, называется вариационным рядом.
Пример 1.
Взята выборка (в алфавитном порядке) наименьших цен в тысячах рублях за 1 м 2 на новое жилье в городах России на май 2016 г. (http://www.rosrealt.ru/):
Построим вариационный ряд.
Элемент выборки 211.5 является аномальным, что объясняется исключительным положением города. Этот элемент следует исключить из выборки.
Тогда вариационный ряд (по определению – в возрастающем порядке) примет вид:
31, 36.5, 45, 47, 48, 52, 56.5, 59, 60.5, 64, 65, 70, 83.5, 94.
Пусть из генеральной совокупности извлечена выборка:
Отношения частот к объему выборки
Статистическим рядом называется вариационный ряд с указанием соответствующих частот или относительных частот.
В общем случае статистический ряд представляют в виде таблицы (варианта – частоты):
| Варианты xi | х1 | х2 | … | х k |
| Частоты ni | n 1 | n 2 | … | nk |
или (варианта – относительные частоты):
| Варианты xi | х1 | х2 | … | х k |
Относительные частоты 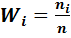 | 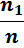 |  | … | 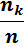 |
Пример 2.
Преобразуем выборку из примера 1 в статистический ряд частот:
| xi | 31 | 36.5 | 45 | 47 | 48 | 52 | 56.5 | 59 | 60.5 | 64 | 65 | 70 | 83.5 | 94 |
| ni | 1 | 1 | 1 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Преобразуем выборку из примера 1 в статистический ряд относительных частот:
| xi | 31 | 36.5 | 45 | 47 | 48 | 52 | 56.5 | 59 | 60.5 | 64 | 65 | 70 | 83.5 | 94 |
| Wi | 1/18 | 1/18 | 1/18 | 3/18 | 2/18 | 2/18 | 1/18 | 1/18 | 1/18 | 1/18 | 1/18 | 1/18 | 1/18 | 1/18 |
Статистический ряд также можно изобразить графически в виде полигона частот или полигона относительных частот, что позволяет получить наглядное представление о закономерности варьирования наблюдаемых значений случайной величины.
Для этого в прямоугольной системе координат наносятся точки с координатами (xi, ni) или (xi, 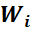
Полученную ломанную линию называют полигоном.
Для примера 2 полигон частот можно представить в виде рисунка 1.
Рисунок 1
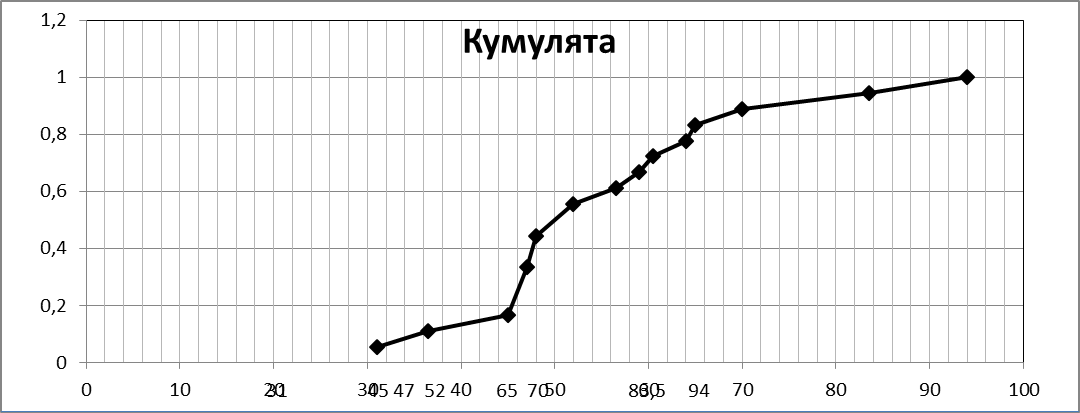
Статистический ряд графически можно изобразить в виде кумулятивной кривой (кривой сумм — кумуляты).
При построении кумуляты дискретного вариационного ряда:
— на оси абсцисс откладывают варианты xi,
— по оси ординат соответствующие им накопленные частоты 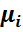
Соединяя точки с координатами (xi 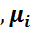
Для получения накопительных частот и дальнейшего построения точек (xi 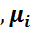
| Варианты xi | х1 | х2 | … | х k |
Относительные частоты 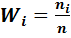 |  | 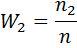 | … | 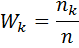 |
Накопительные относительные частоты  = = 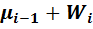 | 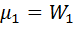 | 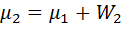 | … | 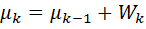 |
График кумуляты дает представление о графике функции распределения F ( X ) генеральной совокупности.
Пример 3.
Для статистического ряда примера 2 составим расчетную таблицу для накопительных частот и построим кумуляту (Рисунок 2).
| xi | 31 | 36.5 | 45 | 47 | 48 | 52 | 56.5 | 59 | 60.5 | 64 | 65 | 70 | 83.5 | 94 |
| Wi | 1/18 | 1/18 | 1/18 | 3/18 | 2/18 | 2/18 | 1/18 | 1/18 | 1/18 | 1/18 | 1/18 | 1/18 | 1/18 | 1/18 |
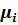 | 1/18 | 2/18 | 3/18 | 6/18 | 8/18 | 10/18 | 11/18 | 12/18 | 13/18 | 14/18 | 15/18 | 16/18 | 17/18 | 18/18= 1 |
Рисунок 2
Вопрос 4. Интервальный статистический ряд
Если выборка получена из непрерывной генеральной совокупности, объем наблюдаемых значений случайной величины большой, то вариационный и статистические ряды будут трудно обозримыми множествами и в этом случае, строят интервальный статистический ряд.
Для построения такого ряда весь интервал варьирования (колеблемости) наблюдаемых значений случайной величины разбивают на ряд частичных интервалов и подсчитывают частоту попадания значений величины в каждый частичный интервал.
Если количество наблюдений n достаточно большое, то есть, ( 
1. Вычисляется размах варьирования R признака Х, как разность между наибольшим 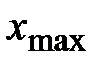
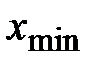
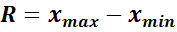
2. Размах R варьирования признака Х делится на k разных частей и таким образом определяется число интервалов в таблице.
Величину k выбирают, пользуясь следующими правилами:
1) 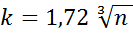
7) k = 1 +3,3 lg n (формула Старджесса).
Длина h каждого частичного интервала определяется по формуле: 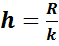
Величину h обычно округляют до некоторого значения d.
если результаты 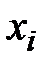
если 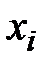
3. Затем подсчитывается частота ni, с которой попадают значения 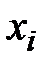
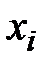
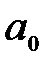
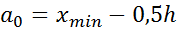
конец 

4. Промежуточные интервалы получают прибавляя к концу предыдущего интервала длину частичного интервала h:

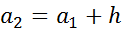
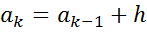
5. Сформированный интервальный вариационный ряд записывают в виде таблицы:
Варианты-интервалы 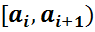 | 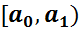 | 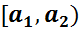 | . |  |
| Частоты ni | n1 | n2 | . | nk |
6. Интервальный вариационный ряд изображают геометрически в виде гистограммы частот ni или гистограммы относительных частот 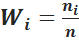
Гистограммой называется ступенчатая фигура, для построения которой по оси Ox откладывают отрезки, изображающие частичные интервалы ( 
Построение интервального статистического ряда рассмотрим на примере.
Пример 4. В результате независимых измерений получены данные:
| 2,1 | 2,3 | 4,2 | 3,7 | 5,5 | 5,3 | 3,4 | 4,7 | 4,4 | 2,6 |
| 4,3 | 4,3 | 5,6 | 4,5 | 4,8 | 5,2 | 4,8 | 4,3 | 3,4 | 4,3 |
| 4,5 | 2,2 | 3,4 | 4,5 | 4,5 | 3,4 | 3,6 | 4,1 | 3,2 | 2,8 |
| 4,3 | 3,5 | 5,3 | 4,6 | 3,9 | 3,5 | 5,7 | 5,1 | 4,2 | 5,8 |
| 2,7 | 4,2 | 4,8 | 3,6 | 3,8 | 5,9 | 3,7 | 2,4 | 4,1 | 5,1 |
1) Объем выборки n=50. Для построения интервального ряда возьмем k=6.
2) Просматривая приведенные результаты наблюдений, находим наименьшее значение выборки 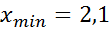
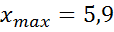
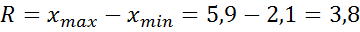
3) Длина частичного интервала 
4) Вычислим 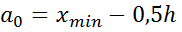
[1,8; 2,5), [2,5; 3,2), [3,2; 3,9), [3,9; 4,6), [4,6; 5,3), [5,3; 6,0].
4) Просматривая результаты наблюдений, определим количество значений признака в каждом полученном интервале. Это можно выполнить в виде таблицы.
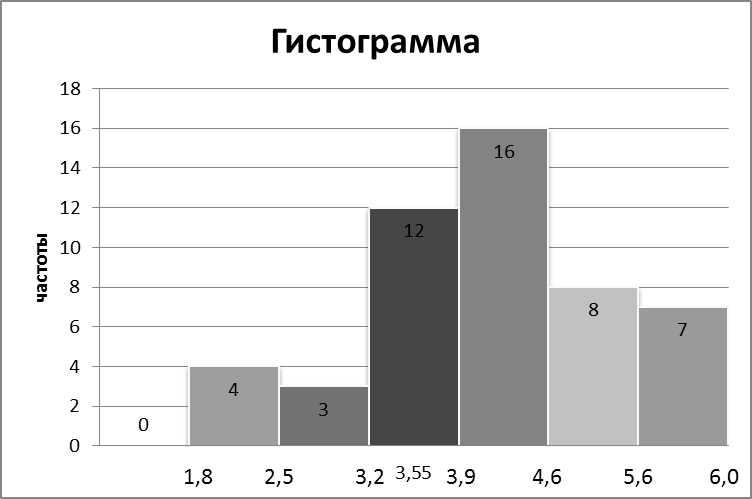
| № п/п i | Интервалы  | Рабочее поле | Частота ni | Относительная частота 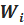 |
| 1 | [1,8; 2,5) | 1111 | 4 | 0,08 |
| 2 | [2,5; 3,2) | 111 | 3 | 0,06 |
| 3 | [3,2; 3,9) | 12 | 0,24 | |
| 4 | [3,9; 4,6) | 16 | 0,32 | |
| 5 | [4,6; 5,3) | 8 | 0,16 | |
| 6 | [5,3; 6,0] | 7 | 0,14 | |
| Сумма | 50 | 1 |
При вычислении относительных частот округление результатов следует проводить таким образом, чтобы общая сумма относительных частот была равна 1.
Построим гистограмму частот интервального статистического ряда.
Вопрос 5. Статистические характеристики выборки
Для дальнейшего изучения изменения значений случайной величины служат числовые характеристики выборки.
Эти характеристики вычисляются по статистическим данным, т.е. данным, полученным в результате наблюдений, поэтому их называют статистическими.
Среди статистических характеристик выделяют:
— характеристики положения выборки (медиана, мода, средняя величина),
— характеристики рассеяния элементов выборки относительно средних величин (дисперсия, среднее квадратическое отклонение).
Пусть выборка объема n представлена в виде статического ряда
| Варианты xi | х1 | х2 | … | х k |
| Частоты ni | n 1 | n 2 | … | nk |
Модой Мо называют варианту, которая имеет наибольшую частоту.
Например, для данного статистического ряда Мо=14
| xi | 4 | 8 | 14 | 19 |
| ni | 3 | 4 | 6 | 5 |
Медианой Meназывают варианту, которая делит статистический ряд на равные части.
При нечетном объеме выборки 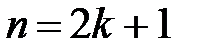
Например, для статистического ряда
| xi | 3 | 5 | 8 | 12 | 15 |
| п i | 6 | 2 | 4 | 5 | 8 |
При четном объеме выборки 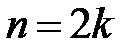
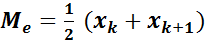
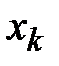
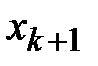
Например, для выборки
| xi | 2 | 5 | 7 | 10 | 12 | 14 |
| ni | 3 | 4 | 8 | 2 | 3 | 6 |
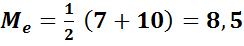
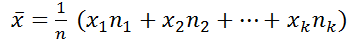
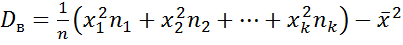

При малом объеме выборки (п≤30) пользуются исправленной выборочной дисперсией 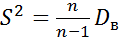
Выборочное среднее квадратическое отклонение
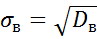

Все статистические характеристики статистического ряда вычисляются по выше приведенным формулам.
Для вычисления статистических характеристик выборки можно использовать готовые компьютерные программы (например, Microsoft Office Excel).
Пример 5. Определим статистические характеристики для выборки из примера 4.
Представим интервальный статистический ряд в виде дискретного ряда, заменив каждый интервал на соответствующую середину.
| № п/п i | Интервалы 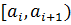 | Середины интервалов xi | Частота ni | Относительная частота 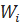 |
| 1 | [1,8; 2,5) | 2,15 | 4 | 0,08 |
| 2 | [2,5; 3,2) | 2,85 | 3 | 0,06 |
| 3 | [3,2; 3,9) | 3,55 | 12 | 0,24 |
| 4 | [3,9; 4,6) | 4,25 | 16 | 0,32 |
| 5 | [4,6; 5,3) | 4,95 | 8 | 0,16 |
| 6 | [5,3; 6,0] | 5,65 | 7 | 0,14 |
| Сумма | 50 | 1 |
Вычисления можно оформить в виде таблицы.
| i | xi | ni | xi ni | xi ni xi = 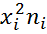 |
| 1 | 2,15 | 4 | 8,6 | 18,49 |
| 2 | 2,85 | 3 | 8,55 | 24,3675 |
| 3 | 3,55 | 12 | 42,6 | 151,23 |
| 4 | 4,25 | 16 | 68 | 289 |
| 5 | 4,95 | 8 | 39,6 | 196,02 |
| 6 | 5,65 | 7 | 39,55 | 223,4575 |
| Сумма | 50 | 206,9 | 902,565 |
Вычислим статистические характеристики для выборки, используя полученные значения:
медиана 
выборочное среднее 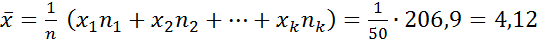
выборочная дисперсия
среднее квадратическое отклонение 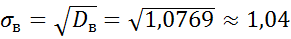
ДОМАШНЕЕ ЗАДАНИЕ
1. Что такое генеральной совокупность, выборка?
2. Сформулируйте определение простого случайного выбора.
3. Дайте определение вариационного ряда.
4. Сформулируйте алгоритм построения статистического ряда.
5. Расскажите о графическом изображении статистического и интервального статистических рядов.
6. Дайте определение кумуляты и расскажите о ее назначении.
7. Дайте определение крайних элементов вариационного ряда, размаха варьирования.
8. По каким формулам находятся выборочные средние статистического распределения?
9. Запишите формулы для вычисления дисперсии для выборки.
10. Запишите формулы для вычисления исправленной дисперсии.
11. Что называется модой, медианой вариационного ряда?
12. Расскажите о нахождении медианы при различном объеме выборки.
13. При изучении некоторой дискретной случайной величины в результате 40 независимых наблюдений получена выборка 10, 13, 10, 9, 9, 12, 12, 6, 7, 9, 7, 8, 8, 9, 13, 14, 9, 11, 9, 8, 10, 10, 11, 11, 11, 12, 8, 7, 9, 10, 14, 13, 8, 8, 9, 10, 11, 11, 12, 12.
Составьте статистический ряд, постройте полигон и кумуляту, вычислите статистические характеристики.
14. Имеются следующие данные о размерах основных фондов (в млн. руб.) 30 предприятий: 4,2; 2,4; 4,9; 6,7; 4,5; 2,7; 3,9; 2,1; 5,8; 4,0; 2,8; 7,3; 4,4; 6,6; 2,0; 6,2; 7,0; 8,1; 0,7; 6,8; 9,4; 7,6; 6,3; 8,8; 6,5; 1,4; 4,6; 2,0; 7,2; 9,1.
Составьте интервальный статистический ряд, постройте полигон и кумуляту, вычислите статистические характеристики.
Дата добавления: 2020-12-22 ; просмотров: 68 ; Мы поможем в написании вашей работы!