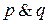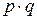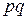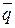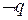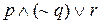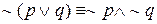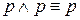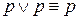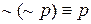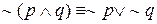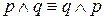Если высказывание o ложно что можно сказать об истинности высказывания i
Если высказывание o ложно что можно сказать об истинности высказывания i
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Если высказывание o ложно что можно сказать об истинности высказывания i
Простые и сложные высказывания, логические переменные и логические константы, логическое отрицание, логическое умножение, логическое сложение, таблицы истинности для логических операций
Для описания рассуждений и правил выполнения действий с информацией используют специальный язык, принятый в математической логике. В основе рассуждений содержатся специальные предложения, называемые высказываниями. В высказываниях всегда что-либо утверждается или отрицается об объектах, их свойствах и отношениях между объектами. Высказыванием является любое суждение, относительно которого можно сказать, истинно оно или ложно. Высказываниями могут быть только повествовательные предложения. Вопросительные или побудительные предложения высказываниями не являются.
Высказывание — суждение, сформулированное в виде повествовательного предложения, о котором можно сказать, истинно оно или ложно.
Например, вопросительные предложения «В каком году было первое летописное упоминание о Москве?» и «Что является внешней памятью компьютера?» или побудительное предложение «Соблюдайте правила техники безопасности в компьютерном классе» высказываниями не являются. Повествовательные предложения «Первое летописное упоминание о Москве было в 1812 г.», «Оперативное запоминающее устройство является внешней памятью компьютера» и «В компьютерном классе не надо соблюдать правила техники безопасности» являются высказываниями, поскольку это суждения, о каждом из которых можно сказать, что оно ложно. Истинными высказываниями будут суждения «Первое летописное упоминание о Москве было в 1147 г.», «Жесткий магнитный диск является внешней памятью компьютера».
Каждому высказыванию соответствует только одно из двух значений: или «истина», или «ложь», которые являются логическими константами. Истинное значение принято обозначать цифрой 1, а ложное значение — цифрой 0. Высказывания можно обозначать с помощью логических переменных, в качестве которых используются заглавные латинские буквы. Логические переменные могут принимать только одно из двух возможных значений: «истина» или «ложь». Например, высказывание «Информация в компьютере кодируется с помощью двух знаков» можно обозначить логической переменной А, а высказывание «Принтер является устройством хранения информации» можно обозначить логической переменной В. Поскольку первое высказывание соответствует действительности, то А = 1. Такая запись означает, что высказывание А истинно. Так как второе высказывание не соответствует действительности, то В = 0. Такая запись означает, что высказывание в ложно.
Высказывания могут быть простыми и сложными. Высказывание называется простым, если никакая его часть не является высказыванием. До сих пор были приведены примеры простых высказываний, которые обозначались логическими перемены ми. Выстраивая цепочку рассуждений, человек с помощью логических операций объединяет простые высказывания в сложнее’ высказывания. Чтобы узнать значение сложного высказывания нет необходимости вдумываться в его содержание. Достаточно знать значение простых высказываний, составляющих сложное высказывание, и правила выполнения логических операций.
Логическая операция — действие, позволяющее составлять сложное высказывание из простых высказываний.
Все рассуждения человека, а также работа современных технических устройств основываются на типовых действиях с информацией — трех логических операциях: логическом отрицании (инверсии), логическом умножении (конъюнкции) и логическом сложении (дизъюнкции).
Логическое отрицание простого высказывания получают добавлением слов «Неверно, что» в начале простого высказывания.
■ ПРИМЕР 1. Имеется простое высказывание «Крокодилы умеют летать». Результатом логического отрицания будет высказывание «Неверно, что крокодилы умеют летать». Значение исходного высказывания — «ложь», а значение нового — «истина».
■ ПРИМЕР 2. Имеется простое высказывание «Файл должен иметь имя». Результатом логического отрицания будет высказывание «Неверно, что файл должен иметь имя». Значение исходного высказывания — «истина», а значение нового высказывания — «ложь».
Можно заметить, что логическое отрицание высказывания истинно, когда исходное высказывание ложно, и наоборот, логическое отрицание высказывания ложно, когда исходное высказывание истинно.
Логическое отрицание (инверсия) — логическая операция, ставящая в соответствие простому высказыванию новое высказывание, значение которого противоположно значению исходного высказывания.
Обозначим простое высказывание логической переменной А. Тогда логическое отрицание этого высказывания будем обозначать НЕ А. Запишем все возможные значения логической переменной А и соответствующие результаты логического отрицания НЕ А в виде таблицы, которая называется таблицей истинности для логического отрицания (табл. 40).
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО ОТРИЦАНИЯ
Если/1 = 0, то НЕ А = 1 (см. пример 1).
Если А = 1, то НЕ А = 0 (см. пример 2)
Можно заметить, что в таблице истинности для логического отрицания ноль меняется на единицу, а единица меняется на ноль.
Логическое умножение двух простых высказываний получают объединением этих высказываний с помощью союза и. Разберем на примерах 3—6, что будет являться результатом логического умножения.
■ ПРИМЕР 3. Имеются два простых высказывания. Одно высказывание — «Карлсон живет в подвале». Другое высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале, и Карлсон лечится мороженым». Можно сформулировать новое высказывание более кратко: «Карлсон живет в подвале и лечится мороженым». Оба исходных высказывания ложны. Значение нового сложного высказывания также «ложь».
■ ПРИМЕР 4. Имеются два простых высказывания. Первое высказывание — «Карлсон живет в подвале». Второе высказывание — «Карлсон лечится вареньем».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет в подвале и лечится вареньем». Первое исходное высказывание ложно, а второе истинно. Значение нового сложного высказывания — «ложь».
■ ПРИМЕР 5. Имеются два простых высказывания. Первое высказывание — «Карлсон живет на крыше». Второе высказывание — «Карлсон лечится мороженым».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится мороженым». Первое исходное высказывание истин но, а второе ложно. Значение нового сложного высказывания «ложь».
Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится вареньем». Оба исходных высказывания истинны. Зпачение нового сложного высказывания также «истина».
Можно заметить, что логическое умножение двух высказываний истинно только в одном случае — когда оба исходных высказывания истинн ы.
Логическое умножение (конъюнкция) — логическая операция, ставящая в соответствие двум простым высказываниям новое высказывание, значение которого истинно тогда и только тогда, когда оба исходных высказывания истинны.
ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО УМНОЖЕНИЯ
Логика высказываний



Введение в математическую логику
Логика, созданная как наука Аристотелем (384–322 г. до н.э.), на протяжении столетий использовалась для развития многих областей знания, включая теологию, философию, математику.
Она – тот фундамент, на котором построено все здание математики. По сути, логика — это наука о рассуждениях, которая позволяет определить истинность или ложность того или иного математического утверждения, исходя из совокупности первичных предположений, называемых аксиомами. Логика применяется также в информатике для построения компьютерных программ и доказательства их корректности. Понятия, методы и средства логики лежат в основе современных информационных технологий. Одна из основных целей этой работы — изложить основы математической логики, показать, как она используется в информатике, и разработать методы анализа и доказательства математических утверждений.
Понятие высказывания
Высказывание — это утверждение или повествовательное предложение, о котором можно сказать, что оно истинно или ложно. Иными словами, утверждение об истинности или ложности высказывания должно иметь смысл. Истинность или ложность, приписываемые некоторому утверждению, называются его значением истинности, или истинностным значением.
Например, высказывания Дважды два четыре и Город Челябинск находится в азиатской части России истинные, а высказывания Три больше пяти и Река Дон в настоящее время впадает в Каспийское море ложны, так как не соответствуют действительности. Истинные высказывания принято обозначать T (true) или И (истина), а ложные, соответственно, F (false) или Л (ложь). В информатике истинность принято обозначать 1 (двоичная единица), а ложность – 0 (двоичный ноль).
Вот примеры предложений, не являющихся высказываниями:
Прочтите эту главу до следующего занятия (приказ или восклицание),
Это утверждение ложно (внутренне противоречивое утверждение),
Площадь отрезка меньше длины куба (нельзя сказать истинно это предложение или ложно, т.к. не имеет смысла).
Мы будем обозначать высказывания буквами латинского алфавита р, q, r, Например, р может обозначать утверждение Завтра будет дождь, а q — утверждение Квадрат целого числа есть число положительное.
Логические связки
Пусть р и q обозначают высказывания
р: Джейн водит автомобиль,
q: У Боба русые волосы.
Джейн водит автомобиль и у Боба русые волосы состоит из двух частей, объединенных связкой и. Это высказывание может быть символически записано в виде
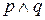
где символ 
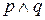
Встречаются также следующие варианты записи конъюнкции:
Точно так же высказывание
Джейн водит автомобиль или у Боба русые волосы.
символически выражается как
где 

Опровержение, или отрицание высказывания p обозначается через
Таким образом, если р есть высказывание Джейн водит автомобиль, то 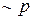
Если r есть высказывание Джо нравится информатика, то Джейн не водит автомобиль и у Боба русые волосы или Джо любит информатику символически запишется как
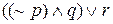
И наоборот, выражение
это символическая форма записи высказывания Джейн водит автомобиль, у Боба волосы не русые и Джо нравится информатика.
Рассмотрим выражение 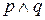
Возможны четыре случая, которые нам необходимо рассмотреть. Высказывание р может быть истинным (Т) или ложным (F) и независимо от того, какое истинностное значение принимает р, высказывание q может также быть истинным (Т) или ложным (F). Таблица истинности перечисляет все возможные комбинации истинности и ложности сложных высказываний.
| Случай | p | q | 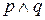 |
| T | T | T | |
| T | F | F | |
| F | T | F | |
| F | F | F |
Итак, конъюнкция 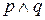
Точно так же рассмотрим высказывание Джейн водит автомобиль или у Боба русые волосы, которое символически выражается как 

| Случай | p | q |  |
| T | T | T | |
| T | F | T | |
| F | T | T | |
| F | F | F |
Дизъюнкция 
Таблица истинности для отрицания 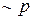
| Случай | p | 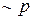 |
| T | F | |
| F | T |
Истинностное значение 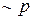
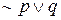


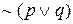
Символы 

является унарной связкой, так как применяется только к одному высказыванию.
Еще одна бинарная связка – это исключающее или, которое обозначается через 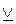
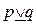
| Случай | p | q |  |
| T | T | F | |
| T | F | T | |
| F | T | T | |
| F | F | F |
Используя слово или, мы можем иметь в виду исключающее или. Например, когда мы говорим, что р — либо истина, либо ложь, то, естественно, предполагаем, что это не выполняется одновременно. В логике исключающее или используется довольно редко, и в дальнейшем мы, как правило, будем обходиться без него.
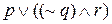
где скобки использованы, чтобы показать, какие именно высказывания являются компонентами каждой связки.
Таблица истинности дает возможность однозначно указать те ситуации, когда высказывание 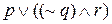
| Случай | p | q | r |  | 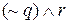 | 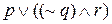 |
| T | T | T | F | F | T | |
| T | T | F | F | F | T | |
| T | F | T | T | T | T | |
| T | F | F | T | F | T | |
| F | T | T | F | F | F | |
| F | T | F | F | F | F | |
| F | F | T | T | T | T | |
| F | F | F | T | F | F |
При нахождении значений истинности для столбца 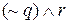



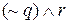

Заметим, что при определении значений истинности для столбца 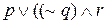
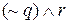

Другой, эквивалентный способ построения таблицы истинности состоит в том, чтобы записывать истинностные значения выражения под связкой. Снова рассмотрим выражение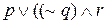
истинностные значения высказывания 
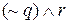

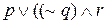

| Случай | p | q | r | p |  | (( | q) |  | r |
| T | T | T | T | T | F | T | F | T | |
| T | T | F | T | T | F | T | F | F | |
| T | F | T | T | T | T | F | T | T | |
| T | F | F | T | T | F | F | F | F | |
| F | T | T | F | F | F | T | F | T | |
| F | T | F | F | F | F | T | F | F | |
| F | F | T | F | T | T | F | T | T | |
| F | F | F | F | F | F | F | F | F |
1.1.3. Условные высказывания
Допустим, некто утверждает, что если случится одно событие, то случится и другое. Предположим, отец говорит сыну: «Если в этом семестре ты сдашь все экзамены на «отлично», я куплю тебе машину«. Заметьте, что высказывание имеет вид: если р, то q, где р — высказывание В этом семестре ты сдашь все экзамены на «отлично», а q — высказывание Я куплю тебе машину. Сложное высказывание мы обозначим символически через 
Самое мягкое, что можно сказать об отце в таком случае, — это то, что он солгал. Следовательно, если р истинно, а q ложно, то 

Поскольку студент не выполнил свою часть соглашения, отец тоже свободен от обязательств. Таким образом, если р и q ложны, то 
Таким образом, таблица истинности для высказывания 
| Случай | p | q |  |
| T | T | T | |
| T | F | F | |
| F | T | T | |
| F | F | T |
Символ 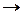
Может показаться, что 
если p, то q или как 
То, что Джейн управляет автомобилем, никак причинно не связано с тем, что Боб русоволосый. Однако нужно помнить, что истинность или ложность бинарного сложного высказывания зависит только от истинности составляющих его частей и не зависит от наличия или отсутствия между ними какой-либо связи.
Рассмотрим следующий пример. Требуется найти таблицу истинности для выражения
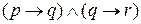
Используя таблицу истинности для 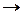

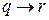
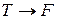
Теперь используем таблицу для 
| Случай | p | q | r | (p | 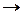 | q) |  | (q | 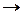 | r) |
| T | T | T | T | T | T | T | T | T | T | |
| T | T | F | T | T | T | F | T | F | F | |
| T | F | T | T | F | F | F | F | T | T | |
| T | F | F | T | F | F | F | F | T | F | |
| F | T | T | F | T | T | T | T | T | T | |
| F | T | F | F | T | T | F | T | T | F | |
| F | F | T | F | T | F | T | F | F | T | |
| F | F | F | F | T | F | T | F | T | F | |
| * |
Высказывание вида 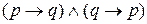
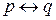
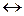
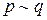
Очевидно, таблица истинности для 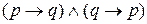
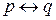
Может возникнуть вопрос о том, как интерпретировать такие выражения, как 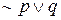
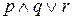
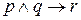
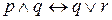
, 

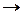
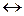

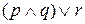
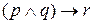
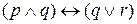
Эквивалентные высказывания
Особый интерес представляют сложные высказывания, имеющие различное строение, но являющиеся истинными в одних и тех же случаях. Такие высказывания называются логически эквивалентными. Эквивалентность двух высказываний легко установить посредством сравнения их таблиц истинности.
Рассмотрим сложные высказывания 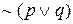

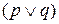
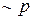


Итак, во всех четырех строках истинностные значения для 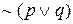

Эквивалентность — очень полезное свойство; используя его, можно строить отрицание высказываний с «или», осуществляя отрицание каждой из его частей и меняя «или» на «и».
С условным высказыванием — импликацией 


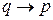
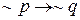

Пусть дано высказывание-импликация Если он играет в футбол, то он популярен. Для этой импликации имеем:
конверсия: Если он популярен, то он играет в футбол
инверсия: Если он не играет в футбол, то он не популярен
контрапозиция: Если он не популярен, то он не играет в футбол
Важно понимать, что высказывания Если он живет в Детройте, то Боб навестит его и Боб навестит его, если он живет в Детройте по сути являются одним и тем же высказыванием. Однако высказывание Если Боб навестит его, то он живет в Детройте не совпадает с предыдущими высказываниями. Не важен порядок, в котором р и q присутствуют в предложении, а важно, какая часть предложения является частью «если», а какая часть является частью «то». Может показаться, что при замене если р, то q на q, если р получается конверсия, но с логической точки зрения последнее высказывание совпадает с исходным.
Эквивалентность и контрапозиция условных высказываний имеют в математике большое значение. Зачастую гораздо легче доказать теорему от противного, чем дать ее прямое доказательство. Используя эквивалентность импликации и ее контрапозиции, нетрудно показать, что конверсия и инверсия импликации имеют одну и ту же таблицу истинности. В то же время импликация и ее конверсия (или инверсия) имеют различные таблицы истинности.
Используя таблицы истинности, можно доказать следующие логические эквивалентности:
а) Законы идемпотентности
б) Закон двойного отрицания
в) Законы де Моргана
г) Свойства коммутативности
д) Свойства ассоциативности