что такое радиан в математике
Радиан
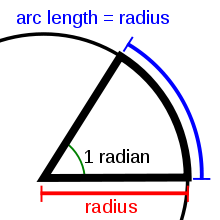
Радиа́н (русское обозначение: рад, международное: rad; от лат. radius — луч, радиус) — основная единица измерения плоских углов в современной математике и физике. Радиан определяется как угловая величина дуги, длина которой равна её радиусу. Таким образом, величина полного угла равна 2 π радиан.
Так как величина угла, выраженная в радианах, равна отношению длины дуги окружности к длине её радиуса, радиан — величина безразмерная. Поэтому обозначение радиана (рад) часто опускается.
Содержание
Связь радиана с другими единицами
Соотношение радиана с другими единицами измерения углов описывается формулой:
Очевидно, 180° = π радиан. Отсюда вытекает тривиальная формула пересчёта из градусов, минут и секунд в радианы и наоборот.
α [рад] = α [°] × ( π / 180); α [°] = α [рад] × (180 / π ),
где α [рад] — угол в радианах, α [°] — угол в градусах
1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″.
Радианная мера в математическом анализе
При рассмотрении тригонометрических функций в математическом анализе всегда считается, что аргумент выражен в радианах, что упрощает запись.
При малых углах синус и тангенс угла, выраженного в радианах, приблизительно равны самому углу, что удобно при приближённых вычислениях:
Косинус малого угла, выраженного в радианах, приближённо равен:
Радиан в физике
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуются с помощью стандартных приставок СИ, однако используются редко. Так, в миллирадианах, микрорадианах и нанорадианах измеряется угловое разрешение в астрономии. В кратных единицах (килорадианах и т. д.) измеряется набег угловой фазы. Сокращённое обозначение (рад, rad) основной и производных единиц не следует путать с устаревшей единицей измерения поглощённой дозы ионизирующего излучения — рад.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 10 1 рад | декарадиан | дарад | darad | 10 −1 рад | децирадиан | драд | drad |
| 10 2 рад | гекторадиан | град | hrad | 10 −2 рад | сантирадиан | срад | crad |
| 10 3 рад | килорадиан | крад | krad | 10 −3 рад | миллирадиан | мрад | mrad |
| 10 6 рад | мегарадиан | Мрад | Mrad | 10 −6 рад | микрорадиан | мкрад | µrad |
| 10 9 рад | гигарадиан | Град | Grad | 10 −9 рад | нанорадиан | нрад | nrad |
| 10 12 рад | терарадиан | Трад | Trad | 10 −12 рад | пикорадиан | прад | prad |
| 10 15 рад | петарадиан | Прад | Prad | 10 −15 рад | фемторадиан | фрад | frad |
| 10 18 рад | эксарадиан | Эрад | Erad | 10 −18 рад | атторадиан | арад | arad |
| 10 21 рад | зеттарадиан | Зрад | Zrad | 10 −21 рад | зепторадиан | зрад | zrad |
| 10 24 рад | йоттарадиан | Ирад | Yrad | 10 −24 рад | йокторадиан | ирад | yrad |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||
Примечания
См. также
Полезное
Смотреть что такое «Радиан» в других словарях:
РАДИАН — РАДИАН, угол, образованный пересечением двух радиусов из центра ОКРУЖНОСТИ, при этом длина дуги, ограниченной этими радиусами, равна длине радиуса. Таким образом радиан единица измерения УГЛА, приблизительно равный 57,296°, а углу 360°… … Научно-технический энциклопедический словарь
РАДИАН — Лапландский бог, берущий, по их верованию, души умерших к себе на небо. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. радиан (лат. radius луч, радиус) мат. единица измерения плоских углов, употребляемая в… … Словарь иностранных слов русского языка
РАДИАН — (от лат. radius луч, радиус) (рад, rad), единица плоского угла; 1 рад равен углу между двумя радиусами окружности, длина дуги между к рыми равна радиусу. 1 рад=57°17 44,8 »3,44•103 угл. минут»2,06•105 угл. секунд»63,7g (см. ГРАД). Физический… … Физическая энциклопедия
радиан — а, м. radian m., нем. Radian <лат. лат. radius луч. Угол, соответствующий дуге, длина которой равна ее радиусу. БАС 1. Лекс. Гранат: радиан; СИС 1937: радиа/н … Исторический словарь галлицизмов русского языка
РАДИАН — РАДИАН, радиана, муж. (от лат. radius луч) (мат.). Единица измерения углов, представляющая собою угол, у которого дуга равна радиусу окружности. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
радиан — сущ., кол во синонимов: 3 • единица (830) • рад (7) • угол (27) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
радиан — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN radian … Справочник технического переводчика
СОДЕРЖАНИЕ
Определение
История
Понятие радиан, в отличие от градуса угла, обычно приписывается Роджеру Котсу в 1714 году. Он описал радиан во всем, кроме названия, и признал его естественность как единицы угловой меры. До того, как термин « радиан» стал широко распространенным, единицу измерения обычно называли круговой мерой угла.
Идея измерения углов по длине дуги уже использовалась другими математиками. Например, аль-Каши (ок. 1400 г.) использовал так называемые части диаметра в качестве единиц, где одна часть диаметра была 1 / 60 радиан. Они также использовали шестидесятеричные единицы диаметра.
Символ единицы
Конверсии
Преобразование радианов в градусы
угол в градусах знак равно угол в радианах ⋅ 180 ∘ π <\ displaystyle <\ text <угол в градусах>> = <\ text <угол в радианах>> \ cdot <\ frac <180 ^ <\ circ>> <\ pi>>>
угол в радианах знак равно угол в градусах ⋅ π 180 ∘ <\ displaystyle <\ text <угол в радианах>> = <\ text <угол в градусах>> \ cdot <\ frac <\ pi><180 ^ <\ circ>>>>
Преобразование радиана в градус
Таким образом, справедливо следующее эквивалентное соотношение:
По определению радиана полный круг представляет:
Объединение обоих вышеуказанных отношений:
2 π рад знак равно 360 ∘ <\ displaystyle 2 \ pi <\ text 

Преобразование радианов в градусы
1.2 рад знак равно 1.2 ⋅ 200 г π ≈ 76,3944 г <\ displaystyle 1.2 <\ text 
Преимущества измерения в радианах
В частности, результаты анализа с участием тригонометрических функций могут быть элегантно сформулированы, когда аргументы функций выражаются в радианах. Например, использование радианов приводит к простой формуле предела
что является основой многих других тождеств в математике, в том числе
Тригонометрические функции также имеют простое и элегантное расширение рядов при использовании радианов. Например, когда x выражается в радианах, ряд Тейлора для sin x принимает следующий вид:
В том же духе математически важные отношения между функциями синуса и косинуса и экспоненциальной функцией (см., Например, формулу Эйлера ) могут быть элегантно сформулированы, когда аргументы функций выражены в радианах (и в противном случае беспорядочно).
Размерный анализ
Хотя полярные и сферические координаты используют радианы для описания координат в двух и трех измерениях, единица измерения получается из координаты радиуса, поэтому мера угла по-прежнему безразмерна.
Использование в физике
Радиан широко используется в физике, когда требуются угловые измерения. Например, угловая скорость обычно измеряется в радианах в секунду (рад / с). Один оборот в секунду равен 2 π радиан в секунду.
Точно так же угловое ускорение часто измеряется в радианах в секунду в секунду (рад / с 2 ).
Кратные SI
Что такое радиан
Радиан, как и градус, является угловой мерой, т. е., величиной, при помощи которой измеряются плоские углы.
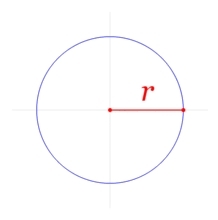
Возьмем окружность, радиусом r:
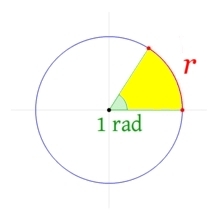
Отложим на окружности дугу, длиной, равной радиусу r, при этом концы дуги соединим с центром окружности:
Это и есть угол в 1 радиан.
1 радиан примерно равен 57°.
Радиан является единицей измерения плоских углов в системах СИ и СГС.
Длина окружности (С) связана с ее радиусом (r) следующим соотношением:
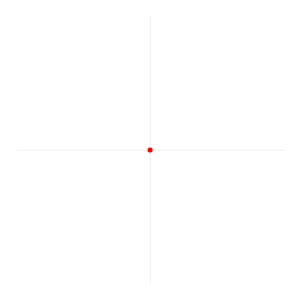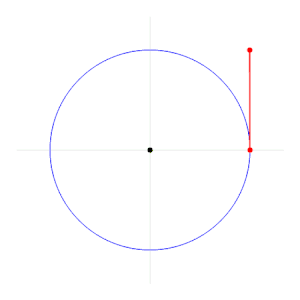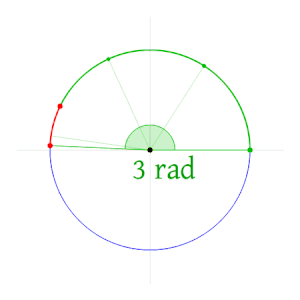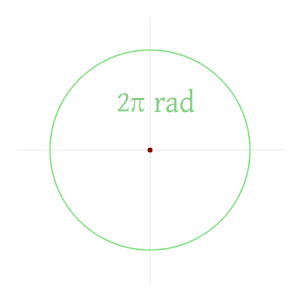
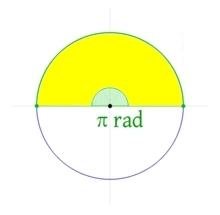
Поэтому, развернутый угол будет опираться на дугу, длина которой будет равна πr, такой угол будет равен π радиан.
Слово «радиан» не принято писать.
Поскольку, на 1° приходится π/180 радиан, то угол в α° будет содержать в α раз больше радиан, чем 1°.
С другой стороны, на 1 радиан приходится (180/π)°, поэтому, на угол β радиан будет приходиться в β раз больше градусов, чем на 1 радиан.
При помощи этих формул легко переводить градусы в радианы и обратно. Например, угол в 60° будет равен:
Угол в 1,5 радиана будет равен:
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:
Код кнопки: 
Политика конфиденциальности Об авторе
Что такое радиан? И почему в круге 360 градусов?
Анна Малкова (автор книги для подготовки к ЕГЭ, ведущая годового Онлайн-курса подготовки к ЕГЭ на 100 баллов, руководитель компании «ЕГЭ-студия» (Курсы ЕГЭ))
Сегодня поговорим об измерении углов. Почему в круге 360 градусов? Что такое 1 радиан? И как связаны градусы и радианы?
Начнем с градусов. Что за странное число 360? Мы привыкли, что в рубле 100 копеек, в метре 100 сантиметров, в килограмме 1000 граммов. У нас десятеричная система исчисления, потому что на руках у нас по 10 пальцев. Но откуда в нашем языке такие странные слова как дюжина, то есть 12? Почему у нас в часе 60 минут, а не 100? И в минуте 60 секунд. Также и этот круг 360 градусов, а не 1000. Дюжина – это 12. 60 делится на 12. Может быть у наших предков было по 12 пальцев на обеих руках? Конечно, нет.
Оказывается, пользуясь пальцами одной руки, можно отсчитать не 5, а 12. Вот как это делали самые разные народы: они считали фаланги пальцев. Их всего 12.
Но чем же число 12 лучше 10? Может быть тем, что у числа 12больше делителей? Посмотрите, на экране делители числа 10 и делители числа 12. А у числа 360 делителей еще больше, целых 24. Если в круге 360 градусов, его легко поделить на множество частей. И это не все.
В день равноденствия солнце встает почти точно на востоке и заходит почти точно на западе, и проходит за день по небу путь в 360 раз больший, чем видимый с Земли диаметр солнца. Небесную полуокружность разделили на 180 градусов. Угловой диаметр солнца примерно 32 угловых минуты, чуть больше, чем полградуса. Он немного меняется в течении года из-за того, что орбита Земли не круговая, а эллиптическая. Утверждение о том, что в день равноденствия солнце проходит по небу путь, равный 360 своим «шагам», то есть 360 видимым диаметрам солнца, верно с некоторой точностью.
– Замечательно! – сказали древние шумеры. – На небе есть подтверждения нашим вычислениям! А вот еще яркая звезда Юпитер!
Оказывается, Юпитер совершает полный оборот вокруг Солнца за 12 лет. Конечно, не 12, а 11,86 земных лет, но очень уж хотелось астрономам округлить до своего любимого числа.
Посмотрим на луну. Ее каждый найдет на небе, когда она полная, в отличии от Юпитера. Лунный месяц примерно 29,5 земных суток. А если у нас в году будет 12 месяце, а год – 365 дней (точнее, конечно, 365,242 земных суток). Что-то близкое к числу 360. Астрономы подумали: «Наверное, Боги хотели, чтобы у нас в году было 360 дней и 12 месяцев по 30 дней, но где-то, вероятно, они ошиблись в расчетах, или кто-то им помешал. Но нам никто не помешает, и мы будем делить круг на 360 градусов».
Обозначается это вот так: 360 и вверху значок градуса.
А что же такое радианы? Что такое угол в 1 радиан? С радианами все намного проще.
1 радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности. 1 радиан приблизительно равен 57 градусам (изображение на экране, 5:20 мин).
А как перевести градусы в радианы? Мы сказали, что 1 круг – это 360 градусов. Но чему же равна длина всей окружности с радиусом r? Вспоминаем формулу (5:44). У нас появляется число Пи. Число Пи известно людям с глубокой древности, потому что люди, видя на небе круглое солнце и луну, хотели сделать что-нибудь похожее. Они плели круглые корзины, делала круглые тарелки. И заметили, что отношение длины окружности к ее диаметру всегда одно и то же. Это число немного больше, чем 3, точнее, 3,1415926. Проходили столетия, и число Пи вычисляли со все большей и большей точностью. Отношение длины окружности к ее диаметру – это число Пи.
Полный круг – 360 градусов. Длина окружности – 2Пиr (6:50).
Наш угол в 1 радиан опирается на дугу окружности равную r. Мы получаем, что угол в один радиан соответствует дуге окружности равной r, радиусу окружности. 360 градусов, полный круг, соответствует всей длине окружности, то есть 2Пиr. Во сколько же раз полный круг больше, чем 1 радиан? Очевидно, в 2Пи раз. 360 градусов соответствует 2Пи радианам. 180 градусов – Пи радиан, 90 градусов – это Пи/2 радиан.
Теперь вы знаете, что же такое написано на Тригонометрическом круге, что такое радианы и почему в круге 360 градусов.
Если у вас есть другие версии, почему именно 360, пишите в комментариях. Присылайте новые интересные вопросы и задачи!
Перевод градусов в радианы и обратно: формулы, примеры
Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.
Связь между градусами и радианами
Связь градусов с радианами
Связь между радианами и градусами выражается формулой
Формулы перевода радианов в градусы и наоборот
Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.
Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
Также можно выразить один градус в радианах.
Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
Значит, в одном радиане примерно 57 градусов
Один градус содержит 0,0175 радиана.
Формула перевода радианов в градусы
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Пример 1. Перевод из радианов в градусы
Применим формулу перехода от радианов к градусам и получим:
Аналогично можно получить формулу перевода из градусов в радианы.
Формула перевода из градусов в радианы
y ° = y · π 180 р а д
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.