что такое погрешность измерения в физике
Погрешности измерений, представление результатов эксперимента
п.1. Шкала измерительного прибора
Примеры шкал различных приборов:
 Манометр – прибор для измерения давления, круговая шкала |  Вольтметр – прибор для измерения напряжения, дуговая шкала |  Индикатор громкости звука, линейная шкала |
п.2. Цена деления
Пример определения цены деления:
 | Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. |
Цена деления: \begin Физическую величину измеряют с помощью прибора Измерение длины бруска линейкой Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений Определение площади столешницы при измеренной длине и ширине Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.) Определяется несовершенством методов и допущениями в методике. Погрешность теории (модели) Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности. Определяется субъективным фактором, ошибками экспериментатора. Примеры значащих цифр: В простейших измерениях инструментальная погрешность прибора является основной. Пример получения результатов прямых измерений с помощью линейки: Второе измерение точнее, т.к. его относительная погрешность меньше. Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки). Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений. Пример расчета истинного значения и погрешности для серии прямых измерений: Составим расчетную таблицу: Сначала находим среднее значение всех измерений: \begin Как найти результат прямого измерения, мы рассмотрели выше. Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса. Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? Составим таблицу для расчета цены деления: Инструментальная точность мензурки равна половине цены деления. Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке. Ответ: Мерой точности является относительная погрешность измерений. Получаем: \begin Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч. Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины. Одна из самых быстрых машин, которую можно встретить на городской дороге, — BMW M8 Competition, — согласно тестированиям автопроизводителя способна разгоняться до 100 км/ч за впечатляющие 2.5 с. Иными словами, вы успеете моргнуть лишь единожды прежде, чем спидометр стильного немецкого купе выдаст отметку «100» и, озорно светя задними габаритными огнями, улетит в закат. Рисунок 1: Панель приборов автомобиля. Спидометр располагается справа. Физические величины различного рода и их измерения так или иначе окружают нас везде. К примеру, та же вышеупомянутая динамика разгона, то есть время, за которое транспортное средство разгоняется до определенной скорости, является важным параметром для любого автомобилиста, приобретающего новенький спорткар в салоне. В жару мы то и дело поглядываем на отметку термометра и ужасаемся, когда температура на отметке безжалостно приближается к 40 °C. Если опаздываем, то обязательно держим под рукой часы и проверяем время по минутам. Если худеем, то каждое утро начинаем со взвешивания и фиксируем массу своего тела в килограммах. Если растем, то периодически интересуемся, сколько на этот раз метров и сантиметров покажет настенная линейка. Правда несмотря на то, что физика относится к наукам точным, как бы удивительно ни было, ни одна ее величина — ни время, ни длина, ни скорость, ни что-либо еще — не может быть выражена с предельной точностью. Ведь вряд ли вы весите, скажем, ровно 60 килограмм без единого лишнего миллиграмма или имеете рост ровно 170 сантиметров. Точно так же, как и BMW M8 Competition не разгоняется до 100 км/ч абсолютно ровно за две с половиной секунды. Точность измерений характеризует близость результата измерения к фактическому значению измеряемой величины. Строго говоря, ни одна физическая величина не может быть измерена с абсолютной точностью — так, чтобы данные измерительного прибора отображали истинное значение. Мир и его явления, на самом деле, практически всегда имеют отношение к иррациональным числам, таким, как, к примеру, результат деления десяти на три: наберите данную операцию на калькуляторе и посмотрите на то, как неэстетично в реальности выглядят данные — с кучей знаков после запятой, за которыми не угнаться. Однако иррациональность чисел не удивляет, да и слишком абстрактна, дабы уловить суть. Что есть деление десяти на три? Тогда, для конкретности, стоит покуситься на святое — на время. Казалось бы, что может быть точнее времени, показываемого самыми точными на свете часами — атомными часами? И тем не менее, даже если вы зайдете на онлайн-ресурс, официально регистрирующий международное атомное время с точностью до миллисекунд, действительного точного измерения времени там вы не найдете. Всегда есть условности: задержка передачи данных между сетевыми элементами; ваш мозг, регистрирующий и обрабатывающий информацию, поступающую через органы чувств и т. д. Все это отдаляет нас, хоть и несущественно, от фактического значения величины. Именно поэтому в физике одним из важнейших понятий является понятие погрешности. Представьте, что вас отправили в магазин купить сахар, но вот незадача: фасованный в пачках как раз закончился и остался только на развес. Что делать, вы просите продавца тогда отмерить вам ровно килограмм. Продавец взял лопатку, наполнил пакет, положил его на весы, и они выдают значение — 1.000 кг. Как удачно положили. Вы рассчитываетесь и счастливым возвращаетесь домой. А теперь представим, что по необыкновенной случайности у вас дома имеются весы, показывающие массу с точностью до миллиграмма. Вы решаете интереса ради перевесить пакет, чтобы посмотреть, действительно ли его масса равна строго килограмму. И какого же удивление, когда более точные весы показывают массу не в 1.000 кг, а в 0.999990 кг. Иными словами, вас обсчитали. Обсчитали, между прочим, на десять миллиграмм! Чем меньше цена деления прибора, тем точнее измерение. Ваши весы с учетом массы до миллиграмма оказались точнее магазинных «граммовых» весов. Однако и это не предел, ведь существуют фармакологические весы, определяющие массу до микрограмма — одной миллиардной килограмма. Так можно продолжать до бесконечности, пока у нас не закончатся технологические возможности сконструировать еще более точные весы. Однако все измерительные приборы, пусть и самые точные, несовершенны. Несовершенно даже само то, как мы видим, слышим и ощущаем мир вокруг. Это, наряду с прочими факторами, приводит к тому, что при измерении величины получается ее приближенное значение, не истинное. Разница между приближенным и истинным значениями и называется погрешностью. Важно. Погрешность не равно ошибке. В обычном, бытовом языке мы привыкли к тому, что слово «погрешность» у нас ассоциируется с просчетом или упущением. В физике погрешность — обыденное явление, присутствующее внутри практически каждой величины, и мало что имеет общего с ошибкой в привычном понимании слова. Все величины, которые, к примеру, вы видите в типовых физических задачах на вычисление, так или иначе содержат погрешность. Ее не обозначают для удобства. Поэтому помните о невозможности проводить эксперименты в идеальных условиях и о том, что ни один прибор чаще всего не сможет показать результат таким, каков он есть на самом деле. Как правило, при однократном проведении измерения определить значение погрешности крайне затруднительно: для ее выявления обычно проводят серию равноточных измерений — измерений, произведенных в одинаковых условиях. После результаты сличаются, то есть сравниваются между собой и, при необходимости, сопоставляются с различными экспериментальными величинами. На основе данных, полученных в результате измерений и сличения, вычисляется погрешность. Обнаружить явление погрешности можно самостоятельно вне строгой лабораторной обстановки: достаточно провести простой эксперимент измерения длины с обычной школьной линейкой. В качестве примера, возьмем карандаш и выполним с ним замеры. Во-первых, необходимо зафиксировать цену деления измерительного прибора. Цена деления определяется разностью двух ближайших отметок. В нашем случае она равна 1 см. Примечание. На разметке измерительного прибора всегда указываются единицы измерения. К примеру, на стандартной линейке можно увидеть пометку «см», сантиметры. Довольно часто используемые для измерений приборы не работают с основными единицами СИ — единицы величин либо являются производными, как сантиметр, либо, как миллиметр ртутного столба, являются внесистемными. Когда вас просят привести ответ в СИ, не забывайте о переводе значений, если измерительный прибор работает с внесистемными или производными единицами. В случае с сантиметровой линейкой, при подобном требовании, обязательно выражение результата в метрах и т. п. Далее совмещаем конец карандаша с нулевой отметкой. Видим, что второй конец располагается между отметками 12 и 13. Какой из этих результатов следует принять за длину нашего карандаша? Очевидно, что тот, который будет ближе к истинному значению — 12 см. Если бы мы провели аналогичный опыт, использовав более точную линейку с ценой деления в миллиметр, мы получили бы значение 12.2 см. Рисунок 3. Замер линейкой с ценой деления 1 мм. А какой из этих результатов лучше будет засчитать теперь? Какой правильный? Оба результата фактически являются верными, их разница заключается лишь в том, что получены они были с разной точностью измерения: длина карандаша во втором варианте была дана с точностью до миллиметра, в первом — до сантиметра. Можно было бы воспользоваться микро́метром, еще более точным измерительными прибором, и получить результат с точностью до микроме́тра. Однако в случае с карандашом точности до миллиметра будет достаточно. Но что делать, если бы мы захотели учесть погрешность? Как ее вычислить и обозначить математически? На самом деле, точно определить погрешность не так просто. Для этого необходимо владение методами математической статистики, для чего требуется уже знание высшей математики. Плюс немаловажно определение комплексных параметров вроде класса точности измерительного прибора. Поэтому для простоты измерений с погрешностью считается, что обычно она равна половине цены деления прибора. В нашем эксперименте при цене деления линейки в сантиметр погрешность составила 0.5 см. При цене деления в миллиметр — 0.05 см. $l$ = 12 ± 0.5 cм — в случае, когда цена деления составляла сантиметр; $l$ = 12.2 ± 0.05 см — в случае, когда цена деления составляла миллиметр. Математический символ плюс-минус (±) используется для обозначения интервала значений и расшифровывается следующим образом: истинное значение величины заключено в диапазоне «от-до». Таким образом, общая формула для записи величин с погрешностью выглядит следующим образом: Выходит, что истинное значение длины карандаша располагается в диапазоне значений от 11.5 см до 12.5 см. При более точных замерах до миллиметра: от 12.15 см до 12.25 см. Однако остается один последний интересный момент. Несмотря на то, что мы провели замеры и определили длину, философски говоря, вопрос остается вопросом: так какую же точную длину имеет карандаш? Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка). В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений». В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы. где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина. Относительная погрешность является безразмерной величиной, либо измеряется в процентах. — если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений; В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора. Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа. Вы будете перенаправлены на Автор24 Погрешностью измерений в физике считается результат измерения физической величины, в независимости от разновидности применения технического средства при измерении. При этом, каким бы тщательным образом не производилось измерение, в результате оно всегда будет отличаться на некоторую величину от своего истинного значения. В зависимости от условий, способствующих проведению соответствующего измерения, а также качества подготовки экспериментатора и вида задействованного при измерении технического средства, будет зависеть погрешность измерений. Погрешность измерения принято считать в физике отклонением значения величины, получившегося после измерения, от ее действительного (истинного) значения. Погрешность измерения представляет собой характеристику точности измерения. При этом, как правило, невозможным становится выяснение с абсолютной точностью истинного значения измеряемой величины. По этой причине становится невозможным и указание степени отклонения полученного при измерении значения от истинного. Подобное отклонение физики называют ошибкой измерения. Оценка величины такого отклонения возможна только посредством задействования статистических методов. На практике истинное значение заменяется использованием значения физической величины, полученного экспериментальным способом и настолько близкого к истинному значению, что в поставленной измерительной задаче смело может применяться вместо него. Подобное значение, зачастую, вычисляется в качестве среднестатистического значения, полученного в момент статистической обработки результатов серии измерений. Такое значение точным не является, но представляет собой наиболее вероятное. По этой причине в измерениях требуется указание степени его точности. С этой целью, наряду с полученным результатом, указывают погрешность измерений. В целях классифицирования погрешностей, в физике применяются следующие признаки: характер проявления, источник появления, условия для проведения измерений, способ выражения, временное поведение величины при измерении. По источнику возникновения определяются такие виды погрешностей: Погрешности средств измерений делят, в зависимости от давления, влажности и температуры, на основную и дополнительную. Дополнительная погрешность, в свою очередь, провоцируется отклонением от нормального значения одной или нескольких влияющих величин. При этом она может оказаться в несколько раз выше основной погрешности. Погрешности измерений разделяются по характеру своих проявлений на: систематические, случайные и грубые. Систематические погрешности считаются составляющими погрешностями измерения, которые сохраняют свое постоянство либо изменяются в случае повторных измерений одной и той же величины, благодаря одним и тем же приборам и посредством одного и того же метода. Систематические погрешности возникают вследствие неправильного градуирования шкалы измерительного прибора и изменения момента противодействия. Случайные погрешности изменяются случайным способом в случае повторных измерений одной и той же величины. Они, в свою очередь, обусловлены неодинаковыми при каждом измерении причинами, и поэтому не могут быть учтены. Грубые погрешности измерений являются погрешностями, превышающими ожидаемые при данных условиях для измерения. Они могут возникать как следствие небрежности экспериментатора или резких изменений условий измерений. В зависимости от временного поведения измеряемой величины при измерении определяется: статистическая погрешность, когда измеряют постоянную во времени величину; динамическая погрешность, когда производится измерение переменной во времени величины, при этом такая погрешность возникает в том случае, когда измерительный прибор не успел отследить изменения измеряемой величины. В зависимости от задействования определенного вида измерения, производится соответствующая оценка погрешностей. Так, в случае использования метода прямого измерения, значение величины определяется непосредственно согласно шкале измерительного прибора, который был задействован в данном случае (динамометра, линейки, часов и др.) При совпадении результатов повторных опытов в пределах максимальной точности измерительного прибора, погрешность измерения считается равнозначной цене деления шкалы прибора. В случае задействования косвенного метода измерения, значение измеряемой величины устанавливается уже не по непосредственным показаниям прибора, а на основании специальных формул, в которые включены значения физических величин, полученных за счет прямых измерений. При определении плотности вещества изначально производят измерение массы и объема тела и далее вычисляют плотность. Одним из максимально упрощенных методов оценки погрешности косвенных измерений считается в физике метод границ, состоящий в том, что посредством специальной формулы, по которой вычисляется измеряемая величина, находятся два ее значения: минимальное и максимальное, и далее вычисляется разница между ними, которая и будет являться истинным значением рассчитываемой величины. Абсолютная погрешность измерения тогда получится при делении величины, полученной при разнице между максимальным и минимальным значением, на два. А среднее значение, в свою очередь, рассчитывается делением суммы максимального и минимального значений величины на два. При этом, округление результатов измерений и вычислений следует производить таким образом, чтобы последняя значащая цифра оказалась в одном с абсолютной погрешностью измеряемой величины десятичном разряде.п.3. Виды измерений
п.4. Погрешность измерений, абсолютная и относительная погрешность
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:п.5. Абсолютная погрешность серии измерений
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.№ опыта 1 2 3 Сумма Масса, г 99,8 101,2 100,3 301,3 Абсолютное отклонение, г 0,6 0,8 0,1 1,5
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin
Поэтому абсолютная погрешность измерения массы: \begin п.6. Представление результатов эксперимента
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.п.7. Задачи
№ мензурки a, мл b, мл n \(\triangle=\frac 1 20 40 4 \(\frac<40-20><4+1>=4\) 2 100 200 4 \(\frac<200-100><4+1>=20\) 3 15 30 4 \(\frac<30-15><4+1>=3\) 4 200 400 4 \(\frac<400-200><4+1>=40\)
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):№ мензурки Объем \(V_0\), мл Абсолютная погрешность
\(\triangle V=\frac<\triangle><2>\), млОтносительная погрешность
\(\delta_V=\frac<\triangle V>1 68 2 3,0% 2 280 10 3,6% 3 27 1,5 5,6% 4 480 20 4,2%
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.Точность и погрешность измерений
Содержание
Что такое точность?
Что такое погрешность?
Эксперимент с линейкой
Рисунок 2. Замер линейкой с ценой деления 1 см.
Вычисление погрешности
Формула погрешности
Погрешности измерений
Содержание
Определение погрешности
Классификация погрешностей
По форме представления

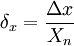
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.По причине возникновения
Погрешность измерения в физике
Понятие погрешности измерения
Готовые работы на аналогичную тему
Классификация погрешностей
Оценка погрешностей измерений
