что такое переменная и постоянная величина
Переменные и постоянные величины
Полезное
Смотреть что такое «Переменные и постоянные величины» в других словарях:
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ — в математике величины, которые в изучаемом вопросе принимают различные значения или сохраняют одно и то же значение. Различие между переменной и постоянной величинами относительно: величина, постоянная в некотором вопросе, может быть переменной в … Большой Энциклопедический словарь
переменные и постоянные величины — (матем.), величины, которые в изучаемом вопросе принимают различные значения или сохраняют одно и то же значение. Различие между переменной и постоянной величинами относительно: величина, постоянная в некотором вопросе, может быть переменной в… … Энциклопедический словарь
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ — см. Константа, Переменная. Философская Энциклопедия. В 5 х т. М.: Советская энциклопедия. Под редакцией Ф. В. Константинова. 1960 1970 … Философская энциклопедия
ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ — (матем.), величины, к рые в изучаемом нопросс принимают разл. значения или сохраняют одно и то же значение. Различие между переменной и постоянной величинами относительно: величина, постоянная в нек ром вопросе, может быть переменной в другом … Естествознание. Энциклопедический словарь
Переменные звёзды — I Переменные звёзды П. з. звезды, видимый блеск которых подвержен колебаниям. Многие П. з. являются нестационарными звездами; переменность блеска таких звезд связана с изменением их температуры и радиуса, истечением вещества,… … Большая советская энциклопедия
Переменные звёзды — I Переменные звёзды П. з. звезды, видимый блеск которых подвержен колебаниям. Многие П. з. являются нестационарными звездами; переменность блеска таких звезд связана с изменением их температуры и радиуса, истечением вещества,… … Большая советская энциклопедия
постоянная величина — см. Переменные и постоянные величины, Константа. * * * ПОСТОЯННАЯ ВЕЛИЧИНА ПОСТОЯННАЯ ВЕЛИЧИНА, см. Переменные и постоянные величины (см. ПЕРЕМЕННЫЕ И ПОСТОЯННЫЕ ВЕЛИЧИНЫ), Константа (см. КОНСТАНТА) … Энциклопедический словарь
Математика — I. Определение предмета математики, связь с другими науками и техникой. Математика (греч. mathematike, от máthema знание, наука), наука о количественных отношениях и пространственных формах действительного мира. «Чистая … Большая советская энциклопедия
Переменная — переменное, одно из основных понятий математики и логики. Начиная с работ П. Ферма, Р. Декарта, И. Ньютона, Г. В. Лейбница и др. основоположников «высшей» математики под П. понимали некоторую «величину», которая может «изменяться»,… … Большая советская энциклопедия
Постоянная величина — константа, величина, которая в изучаемом вопросе сохраняет одно и то же значение (см. Переменные и постоянные величины). Постоянство величины х символически записывают х = const. П. в. часто обозначают буквами С и К … Большая советская энциклопедия
Постоянные и переменные величины
Существуют постоянные и переменные величины. Постоянные – это те величины, которые при заданном условии не меняют своего значения. Переменными величинами называются тогда, когда приобретаются разные значения.
Постоянная величина
Постоянная величина – это величина, которая при заданных условиях не меняет своего значения.
Чтобы убедиться, что постоянная величина существует, вспомним несколько известных примеров: отношение длины круга к диаметру, как известно, равняется ; сумма внутренних углов треугольника равна
; черырехугольника –
; скорость света в вакууме
км/с, постоянным есть ускорение земного притяжения в данной точке Земли и т. п.
Постоянная величина обозначается начальными буквами латинского алфавита – .
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Переменная величина
Рассмотрим переменную величину на примере: в процессе движения точки переменными есть пройденный точкой путь, её координаты, относительно заданной системы координат и т. п.
Переменная величина записывается последними буквами латинского алфавита – . Среди переменных величин удобно выделить такие, что приобретают отдельные изолированные значения, например, значение натуральных чисел
, или значения некоторой последовательности, например, арифметической или геометрической прогрессий. Такие переменные принято обозначать
и называть дискретными переменными.
Если переменная величина приобретает все значения с некоторого промежутка, тогда считают, что она меняется непрерывно. Например, длина столбика термометра при перемене температуры принимает все значения с некоторого отрезка. Посмотрите ниже, как это выглядит на примере.
Пусть и
– действительные числа,
, им отвечают точки на числовой оси.
Отрезком называется множество чисел (точек)
что удовлетворяют условия
, при этом пишут ещё
.
Интервалом называется множества чисел
, что удовлетворяют условия
. Множество всех действительных чисел (точек числовой прямой) будем обозначать интервалом
, это означает, что для переменной
выполняется неравность
. Интервал
– это множество чисел, которые больше
, или множество чисел, что удовлетворяют неравности
Аналогично интервал
означает множеству точек
таких, что
.
Полуинтервалами или
называется множество точек, для которых соответственно
или
.
Отрезок, интервал или полуинтервал мы будем называть ещё промежутком. Промежутки перемены переменной могут появляться, например, при решении неравенств, которые в свою очередь появляются при исследовании функции.
Примеры решений по теме : “Постоянные и переменные величины”
Задача
Решение
Ответ
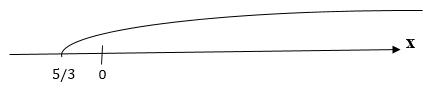
Область решений – промежуток: .
Задача
Определить промежутки перемены переменной , которые заданы неравенством:
Решение
.
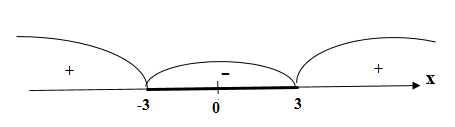
Неравенство решается методом интервалов, определяя знак выражения в “пробных” точках каждого из интервалов.
Ответ
Область решений – отрезок или
.
Задача
Определить промежутки перемены переменной , которые заданы неравностью:
Решение
Для решения двойного неравенства отнимем из всех её частей по 5 и разделим на (-2) (при делении знаки неравенств меняются с отрицательного числа на противоположное).
Ответ
Переменные и постоянные величины
Вы будете перенаправлены на Автор24
Переменные и постоянные величины – это не совсем просто
Школьная математика всегда убеждала и продолжает убеждать нас в том, что вопрос о переменных и постоянных величинах решается очень просто. Переменными считаются величины, которые в условиях данной задачи могут принимать различные значения. Постоянными считаются величины, которые в условиях данной задачи свои значения не меняют.
При этом дополнительно сообщается, что деление величин на переменные и постоянные достаточно условно и зависит от обстоятельств, сопровождающих процесс решения задачи. Одна и та же величина, которая в одних условиях считалась постоянной, в других условиях должна рассматриваться как переменная. Классический пример: сопротивление проводника считается постоянным, пока мы не оказываемся вынужденными учитывать зависимость величины его сопротивления от температуры окружающей среды.
Но, как показывает практика, всего вышеуказанного для корректного решения той или иной задачи бывает недостаточно.
Что такое величина, каждому ясно интуитивно. Уточним это понятие.
В общем случае содержанием процесса решения задачи есть преобразование величин. При этом следует понимать, что в общефилософском смысле величина, представляющая результат решения задачи, уже содержится в её формулировке в неявном виде. Нужно только правильно построить процесс преобразования величин задачи, чтобы этот результат представить явно.
Будем называть величиной любой математический объект, который несет (или может нести) информацию о том или ином значении.
Форма представления величин может быть различной. Например, величина с числовым значением, равным действительной единице, может быть представлена десятичной константой 1,0, функцией Cos(0), а также арифметическим выражением 25,0 – 15,0 – 9,0.
Значения величин можно менять. Так, в результате выполнения действия x = 1,0 величина в форме переменной x оказывается носителем значения действительной единицы. При этом предыдущее значение переменной x теряется. Приведённые примеры уже несколько с иных позиций показывают, что величины могут быть переменными и постоянными.
Готовые работы на аналогичную тему
Переменные величины обладают тем свойством, что их значения могут быть изменены в результате выполнения тех или иных действий. И это значит, что понятие “переменная величина” отражает возможность, но не факт изменения.
Постоянной величиной (константой) следует считать ту, значение которой, в отличие от переменной, изменить принципиально невозможно.
Например, значение постоянной величины в виде выражения 12+3 равно 15, и изменить его нельзя. При этом необходимо фиксировать смысл знаков, с помощью которых представляется величина. В противном случае, если считать, например, знаки этого выражения цифрами в системе счисления с основанием 5, то тогда его значение окажется равным 10.
Итак, в математических текстах носителями значений, то есть величинами, являются переменные, константы, обращения к функциям (или просто функции), а также выражения.
Особенности переменных
Обозначения, с которыми связываются определённые значения, в математике называют переменными (термин употребляется как имя существительное).
Например, значение переменной величины x+1 зависит от значения, связанного с обозначением x. Здесь обозначение x используется в качестве переменной. Изменив значение переменной x, мы тем самым изменим и значение переменной величины x+1.
Таким образом, значения переменных величин зависят от значений переменных, которые входят в их состав. Отличительным свойством переменной является то, что конкретное её значение должно быть ей просто приписано (назначено).
Математический подход, определяющий возможность вычисления значений переменных, в данном контексте оказывается неправильным. В математике можно вычислять только значения выражений.
Основное условие использования переменной в математических текстах в окончательном виде таково: для обращения к переменной достаточно указать её обозначение.
Особенности констант
В математических текстах могут быть использованы две разновидности констант: константы-лексемы и именованные константы.
Кстати, программисты на языках высокого уровня, пользуются этим на вполне формальных (законных) основаниях.
С помощью констант-лексем значения постоянных величин указываются непосредственно без выполнения каких-либо операций. Например, для получения значения постоянной величины 12+3, которая является выражением, необходимо выполнить сложение двух констант-лексем 12 и 3.
Именованная константа представляет собой обозначение, сопоставленное конкретному значению, указанному в виде константы-лексемы.
Помимо компактной записи выражений, именованные константы обеспечивают наглядность и значительные удобства в работе с математическими текстами.
Своё значение именованная константа приобретает как результат предварительной договорённости.
Важное свойство любой именованной константы состоит в том, что её значение не рекомендуется менять в пределах некоторого математического текста.
Выражения
Выражения являются составными частями подавляющего большинства математических текстов. С помощью выражений задают порядок вычисления новых значений на основании других заранее известных значений.
В общем случае в составе выражений используют операнды, знаки операций и регулирующие круглые (квадратные, фигурные) скобки.
Операнды – это общее название объектов, значения которых используют при выполнении операций. Операндами могут быть переменные, константы и функции. Кстати, этот термин весьма популярен в среде программистов. Фрагмент выражения, заключённый в регулирующие скобки, рассматривается как отдельный составной операнд.
Знак операции символизирует вполне определённую совокупность действий, которые должны быть выполнены над соответствующими операндами. Регулирующие скобки устанавливают нужный порядок выполнения операций, который может отличаться от предусмотренного приоритетом операций.
Простейшим случаем выражения является отдельный операнд. В таком выражении нет знаков операций.
Операнд-функция имеет свои особенности. Как правило, такой операнд представляет собой наименование (или знак) функции с последующим указанием в круглых скобках перечня её аргументов. В данном случае круглые скобки являются неотъемлемой принадлежностью функций и к регулирующим не относятся. Отметим, что во многих случаях в операндах-функциях обходятся без скобок (например, 5! – вычисление факториала целого числа 5).
Математические операции
Основные особенности математических операций таковы:
Таблица знаков некоторых операций и уровней приоритетов
Правила вычисления сложного выражения, содержащего цепочку операций при отсутствии регулирующих скобок, следующие:
При наличии регулирующих скобок выражение содержит составные операнды, значения которых должны быть вычислены в первую очередь.
Некоторые особенности записи математических выражений:
Постоянная и переменная величина.
Развитие математики в изучении законов природы и использования этих законов в технике привело к вводу понятий переменной и постоянной величин.
Переменные и постоянные величины. Эти величины в вопросе, который изучается, имеют разные значения или, что относится к постоянной величине, остаются с одним значением постоянно. К примеру, когда изучается падение тела, расстояние до земли, а так же скорость падения — величина переменная, в то время как ускорение (только есть не брать в учет воздушное сопротивление) — постоянная величина.
Поговорим о переменной величине. В условиях нашего вопроса может принять разные значения.
И о постоянной величине. При условии нашего вопроса остается без изменений. Однако одна величина в разных ситуациях может оказаться переменной либо постоянной.
Например, температура T кипения воды в основном это постоянная величина со значением T = 100 °С. Но в ситуациях, когда необходимо учитывать изменения атмосферного давления, температура кипения воды становится переменной величиной.
Областью изменения переменной величины называется совокупность всех принимаемых ею числовых значений. Область изменения может состоять как из одного или нескольких промежутков, так и из одной точки.
Разделение величин переменных и постоянных зачастую применяют в высшей математике, в то время как в элементарной математике в основном разделение величин происходит на известные и неизвестные. Разделение на известные и неизвестные величины есть и в высшей математике, однако занимает не главное место.
Что такое переменная и постоянная величина
рЕТЕНЕООЩЕ Й РПУФПСООЩЕ ЧЕМЙЮЙОЩ
ч ТЕЪХМШФБФЕ ЙЪНЕТЕОЙС ЖЙЪЙЮЕУЛЙИ ЧЕМЙЮЙО (ЧТЕНС, РМПЭБДШ, ПВЯЕН, НБУУБ, УЛПТПУФШ Й Ф.Д.) ПРТЕДЕМСАФУС ЙИ ЮЙУМПЧЩЕ ЪОБЮЕОЙС. нБФЕНБФЙЛБ ЪБОЙНБЕФУС ЧЕМЙЮЙОБНЙ, ПФЧМЕЛБСУШ ПФ ЙИ ЛПОЛТЕФОПЗП УПДЕТЦБОЙС. ч ДБМШОЕКЫЕН, ЗПЧПТС П ЧЕМЙЮЙОБИ, НЩ ВХДЕН ЙНЕФШ Ч ЧЙДХ ЙИ ЮЙУМПЧЩЕ ЪОБЮЕОЙС. ч ТБЪМЙЮОЩИ СЧМЕОЙСИ ОЕЛПФПТЩЕ ЧЕМЙЮЙОЩ ЙЪНЕОСАФУС, Б ДТХЗЙЕ УПИТБОСАФ УЧПЕ ЮЙУМПЧПЕ ЪОБЮЕОЙЕ. оБРТЙНЕТ, РТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ ЧТЕНС Й ТБУУФПСОЙЕ НЕОСАФУС, Б УЛПТПУФШ ПУФБЕФУС РПУФПСООПК.
ъБНЕФЙН, ЮФП Ч НБФЕНБФЙЛЕ РПУФПСООБС ЧЕМЙЮЙОБ ЮБУФП ТБУУНБФТЙЧБЕФУС ЛБЛ ЮБУФОЩК УМХЮБК РЕТЕНЕООПК, Х ЛПФПТПК ЧУЕ ЮЙУМПЧЩЕ ЪОБЮЕОЙС ПДЙОБЛПЧЩ.
пВМБУФША ЙЪНЕОЕОЙС РЕТЕНЕООПК ЧЕМЙЮЙОЩ ОБЪЩЧБЕФУС УПЧПЛХРОПУФШ ЧУЕИ РТЙОЙНБЕНЩИ ЕА ЮЙУМПЧЩИ ЪОБЮЕОЙК. пВМБУФШ ЙЪНЕОЕОЙС НПЦЕФ УПУФПСФШ ЛБЛ ЙЪ ПДОПЗП ЙМЙ ОЕУЛПМШЛЙИ РТПНЕЦХФЛПЧ, ФБЛ Й ЙЪ ПДОПК ФПЮЛЙ.
хРПТСДПЮЕООБС РЕТЕНЕООБС ЧЕМЙЮЙОБ. юЙУМПЧБС РПУМЕДПЧБФЕМШОПУФШ.

оБРТЙНЕТ, ЮЙУМПЧХА РПУМЕДПЧБФЕМШОПУФШ ПВТБЪХАФ УМЕДХАЭЙЕ ЧЕМЙЮЙОЩ:
ъБНЕФЙН, ЮФП ЮЙУМПЧБС РПУМЕДПЧБФЕМШОПУФШ ФБЛЦЕ СЧМСЕФУС ЖХОЛГЙЕК, ПВМБУФШ ПРТЕДЕМЕОЙС ЛПФПТПК УПЧРБДБЕФ У НОПЦЕУФЧПН ОБФХТБМШОЩИ ЮЙУЕМ.
л ПУОПЧОЩН ЬМЕНЕОФБТОЩН ЖХОЛГЙСН ПФОПУСФУС ЧУЕ ЖХОЛГЙЙ, ЙЪХЮБЕНЩЕ Ч ЫЛПМШОПН ЛХТУЕ НБФЕНБФЙЛЙ:
ьМЕНЕОФБТОПК ЖХОЛГЙЕК ОБЪЩЧБЕФУС ЖХОЛГЙС, ЛПФПТБС НПЦЕФ ВЩФШ ЪБДБОБ ПУОПЧОЩНЙ ЬМЕНЕОФБТОЩНЙ ЖХОЛГЙСНЙ Й РПУФПСООЩНЙ РТЙ РПНПЭЙ ЛПОЕЮОПЗП ЮЙУМБ ПРЕТБГЙК УМПЦЕОЙС, ЧЩЮЙФБОЙС, ХНОПЦЕОЙС, ДЕМЕОЙС Й ЧЪСФЙС ЖХОЛГЙЙ ПФ ЖХОЛГЙЙ.