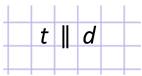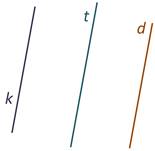что такое параллельные прямые 6 класс
Что такое параллельные прямые 6 класс
Параллельные прямые — две прямые, которые лежат в одной плоскости и не пересекаются, а || b.
Слово «параллельный» от греческого «parallelos» — идущий рядом. Знак параллельности || впервые встречается в трудах У. Оутреда (1677 г).
Выделенная синим цветом часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского. В геометрии Лобачевского через точку, лежащую за прямой, проходит множество прямых, которые не пересекают данную прямую.
Иногда Аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.
Примечание. В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.
Свойства и признаки параллельных прямых

Теорема Фалеса:
Если на одной из двух прямых отложено несколько равных отрезков и через их концы проведены параллельные прямые, не пересекающие другую прямую, то и на ней отложатся равные отрезки.
Это конспект по теме «Параллельные прямые». Выберите дальнейшие действия:
Урок 45 Бесплатно Параллельные прямые
На этом уроке разберем один из случаев взаимного расположения прямых на плоскости, узнаем, какие прямые называют параллельными.
Дадим представление об основных свойствах и признаках параллельных прямых.
Рассмотрим, с помощью каких инструментов и какими способами можно построить их на плоскости.
Убедимся на примерах в том, что знания о параллельных прямых используются во многих областях нашей жизни.
Параллельные прямые
Из всех известных нам линий самой простой на первый взгляд является прямая линия.
Прямая линия бесконечна, то есть не имеет начала и конца.
Следовательно, изобразить на плоскости мы можем только часть прямой, а общий вид ее мы можем только представить.
Прямую обозначают любой строчной латинской буквой и читают как «прямая а». Но прямая может быть обозначена двумя прописными латинскими буквами, которые располагаются на разных концах прямой, и читают её как «прямая АВ».
Прямая линия имеет такие характерные особенности:
Через две произвольные точки можно провести прямую и притом только одну.
Через произвольную точку можно провести бесконечное множество прямых.
Две не совпадающие прямые на плоскости или пересекаются, или не пересекаются.
Прямые, лежащие в одной плоскости и непересекающиеся на всем своем протяжении, называются параллельными прямыми.
У меня есть дополнительная информация к этой части урока!
Слово «параллельность» («параллелос») с греческого языка переводится как «идущие рядом».
Термин «параллельность» использовали еще за долго до того, как параллельные прямые приобрели свое определение.
В древности знак для обозначения параллельных прямых имел вид знака, известного нам сегодня, как знак равенства «=».
Например, параллельность прямых а и d записывали так: «а = d».
Но в 1557 году Роберт Рекорд для обозначения равенства ввел знак «равно» в том виде, в котором он сегодня известен нам «=».
Чтобы избежать недоразумений и путаницы, символ параллельности был перевернут вертикально, его стали обозначать «||»
Сейчас параллельность прямых а и d записывают так: «а||d».
Принято считать, что между параллельными прямыми угол равен нулю.
Отрезки, лежащие на параллельных прямых, называются параллельными друг другу.
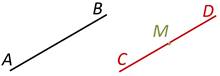
Отрезки AB и CD параллельны (AB||CD).
Отрезки OM и CD не являются параллельными.
Лучи, лежащие на параллельных прямых, называются параллельными друг другу.
Луч а и b параллельны (а||b).
Аналогично определяется параллельность отрезка и прямой, отрезка и луча, луча и прямой.
Необходимо понимать, что нельзя считать отрезки и лучи параллельными друг другу только за то, что они не пересекаются.
Приведем пример непересекающихся отрезков и лучей, которые вовсе не параллельны друг другу.
Как мы можем заметить, отрезок АВ не пересекает луч (а), но он и не параллелен ему.
Таким образом, отрезки и лучи, лежащие на одной прямой или на параллельных прямых, будут являться параллельными друг другу и этим прямым.
Выясним некоторые признаки и свойства параллельных прямых.
Рассмотрим аксиому параллельности прямых:
Через точку, не лежащую на прямой, можно провести только одну прямую, параллельную данной.
Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой прямой, параллельной данной.
Таким образом, расстояние между параллельными прямыми везде одинаково, а длина отрезка перпендикуляра, заключенного между двумя параллельными прямыми, есть расстояние между ними.
Подобную ситуацию можно представить, вспомнив железнодорожный путь (рельсы и шпалы) или шведскую лестницу.
Рассмотрим некоторые признаки параллельных прямых:
1. Если две прямые параллельны третьей прямой, то они между собой параллельны
Если а||с и b||с, то а||b.
2. Если две прямые перпендикулярны третьей, то эти две прямые параллельны друг другу.
Если а⊥с и b⊥с, то а||b.
Перейдем к знакомству со свойствами параллельных прямых.
1. Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и ко второй.
Если c||b и а⊥с, то а⊥b.
2. Если несколько параллельных прямых пересечь прямой, то эта прямая пересечет каждую из параллельных прямых, причем под одним и тем же углом.
∠1 = ∠2 = ∠3
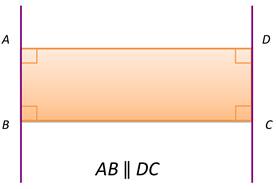
Части параллельных прямых, замкнутые между другими параллельными прямыми, равны.
Если а||b и d||c, а⊥с, b⊥c, b⊥d, a⊥d, то отрезки AB = CD и AC = BD.
Верно и обратное утверждение, если противоположные части четырех пересекающихся прямых равны, то эти части параллельны.
Подобную ситуацию можно представить, вспомнив четырехугольную столешницу или табурет.
Существуют другие признаки и свойства параллельных прямых, но они будут рассмотрены вами позже.
У меня есть дополнительная информация к этой части урока!
Главный труд древнегреческого математика Евклида «Начала» (300 лет до н.э.) является первым дошедшим до наших дней теоретическим трактатом по математике, он содержит основы античной геометрии и математики.
В «Началах» Евклид обобщил все ранее известные достижения древнегреческой математики и создал основу для ее дальнейшего изучения и развития.
Главное научное и историческое значение данной работы Евклида заключается в попытках построения теории геометрии на основе аксиом и логических рассуждений.
Изложение материала ведется от общего к частному: определения и аксиомы, далее постулаты, затем задачи и теоремы.
Евклид делает понятия аксиома и постулат различными, но это различие неясно.
Особый интерес и внимание у математиков всех времен и народов вызывала пятая аксиома о параллельных прямых, описанная в первой из тринадцати книг «Начала».
Пятый постулат Евклида о параллельных прямых, в отличие от остальных простых и элементарных для понимания постулатов, казался громоздким и, на первый взгляд, не очень очевидным.
В связи с этим многие математики пытались доказать недоказуемое и вывести постулат из разряда аксиом и представить как теорему.
Любые доказательства сводились к появлению только лишь более простых формулировок постулата.
За два тысячелетия было огромное множество попыток доказать пятый постулат, но каждая из них содержала утверждение, которое невозможно было доказать без использования того самого постулата.
Научные труды «Начала» оказали заметное влияние на развитие теории математики вплоть до наших дней.
Книга была переведена на множество языков.
В современных источниках приводится другая формулировка постулата о параллельных прямых, которая равносильна постулату Евклида.
Принадлежит она Птолемею Проклу: «В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной»
Существуют и другие эквивалентные формулировки.
Пройти тест и получить оценку можно после входа или регистрации
Параллельные прямые

Всего получено оценок: 96.
Всего получено оценок: 96.
Параллельные прямые находятся повсюду в нашей жизни. Они – основа симметрии, которая, так или иначе, присутствует в каждом элементе мебели, архитектуре и орудиях труда. Знание определения и свойств параллельных прямых помогают не только при решении задач по математике 6 класса, но и при расчетах реальных предметов быта.
Что такое параллельные прямые
Параллельными прямыми называют прямые, которые не пересекаются.
В этом определении параллельных прямых есть небольшая неточность: прямые, которые имеют больше одной общей точки, совпадают. Иногда о них также говорят, как о параллельных.
Прямая, пересекающая параллельные прямые, называется секущей. При пересечений образуется 8 углов. Друг относительно друга они могут быть соответственными, односторонними и накрест лежащими. Рассмотрим их на примере.
Аксиома параллельных прямых
Аксиома параллельных прямых – это одно из основных утверждений геометрии. Через точку можно провести прямую, параллельную данной, и при том только одну – это наиболее распространенная формулировка аксиому.
Из аксиомы есть два следствия:
Обратите внимание, что аксиома справедлива только для плоскости. В пространстве может быть вариант, когда прямая параллельна плоскости, в которой будет бесконечное множество параллельных ей прямых, проходящих через одну точку. Значит в пространстве это условие не обязательно выполняется.
Расстояние между параллельными прямыми в любой точке будет одинаковым и равным величине отрезка, перпендикулярного каждой из прямых.
Фигуры с параллельными прямыми
Существует множество фигур, при построении которых используются параллельные прямые. Например, параллелограмм состоит из двух попарно параллельных отрезков.
Квадрат и прямоугольник также состоят из попарно параллельных прямых, но при этом они являются частным случаем параллелограмма.
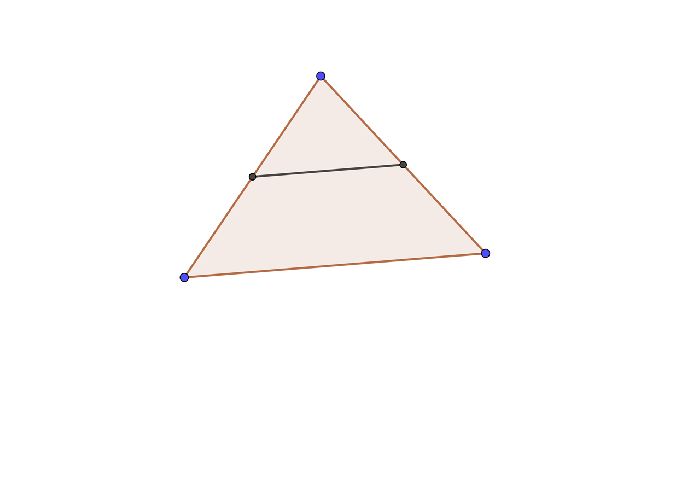
В треугольнике средняя линия всегда параллельна основанию.
Рис. 2. Средняя линия треугольника.
Также есть еще одна интересная фигура: трапеция. В трапеции большое и малое основание параллельны друг другу, а боковые стороны не параллельны.
Если прямые непараллельны, то они пересекаются, но если не параллельны отрезки, это вовсе не значит, что они пересекутся. Отрезки имеют конечное значение длинны, а поэтому могут просто стоять отдельно друг от друга. При этом, отдельных видов или каких-либо таблиц параллельных прямых нет, и вряд ли они когда-нибудь появятся.
Что мы узнали?
Мы узнали все о параллельных прямых, привели аксиому параллельных прямых и следствия из нее. Поговорили о различии понятий параллельных прямых и параллельных отрезков, а также выяснили, почему аксиома для параллельных прямых работает только на плоскости. Привели примеры фигур, для построения которых требуются параллельные прямые.
Параллельность прямых
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Параллельные прямые
Урок 45. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Параллельные прямые»
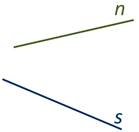
Две прямые на плоскости могут либо пересекаться, либо не пересекаться.
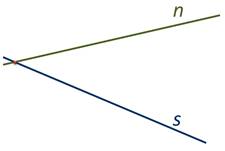
Даже если на рисунке мы не видим точку пересечения прямых n и s, это не значит, что они не пересекаются вовсе. Помните, что прямые можно бесконечно продлевать в обе стороны.
А значит, продлив прямые, мы найдём точку пересечения прямых.
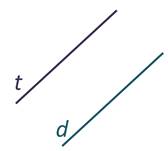
А вот прямые t и d не пересекутся никогда.
Такие прямые называют параллельными.
Таким образом, две непересекающиеся прямые на плоскости называются параллельными.
На рисунке прямая t параллельна прямой d.
В математике слово “параллельные” обозначают специальным символом:
В математике вы уже не раз встречались с параллельными прямыми.
Например, если продлить противоположные стороны прямоугольника, то полученные прямые будут параллельны.
Кроме того, представление о параллельных прямых мы можем получить, если посмотрим на железнодорожные рельсы или на электрические провода.
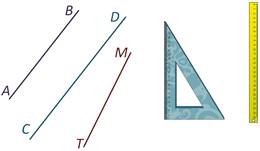
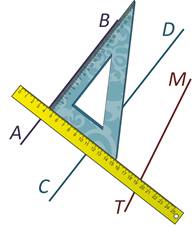
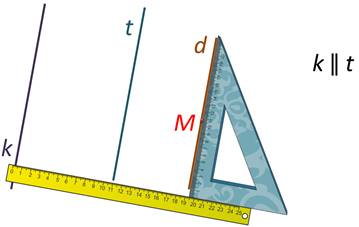
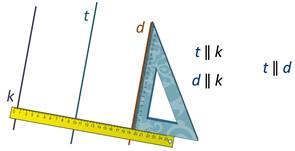
Убедиться в том, что две прямые параллельны можно с помощью чертёжного треугольника и линейки.
Давайте определим, параллельна ли прямая АВ прямой СD, параллельна ли прямая АВ прямой МТ. Для этого берём чертёжный треугольник и совмещаем сторону прямого угла чертёжного треугольника с прямой АВ. К другой стороне угольника прикладываем линейку.
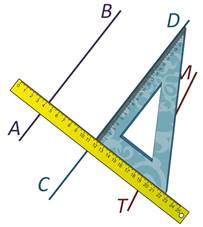
Теперь двигаем угольник вдоль линейки до прямой СD.
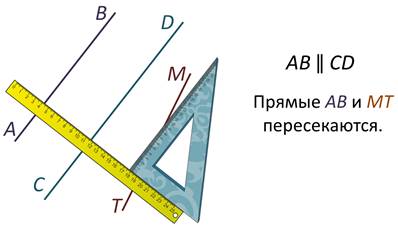
Двигаемся до прямой МТ.
Прямая АВ не параллельна прямой МТ.
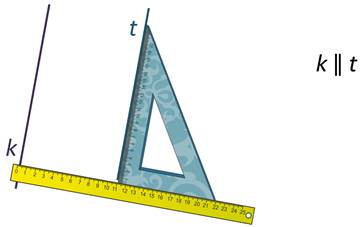
Построить параллельные прямые не сложно.
Для построения прямой линии, параллельной прямой k, надо приложить угольник к прямой k, к другой стороне угольника прикладываем линейку. Теперь двигаем угольник вдоль линейки. Проводим прямую t вдоль другой стороны угольника.
Если нам нужно провести прямую через определённую точку, мы будем действовать так же: прикладываем угольник и линейку; затем, передвигая угольник вдоль линейки, добьёмся того, чтобы точка М оказалась на стороне угольника; теперь проведём прямую d.
Построение параллельных прямых закончено.
Обратите внимание, что через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
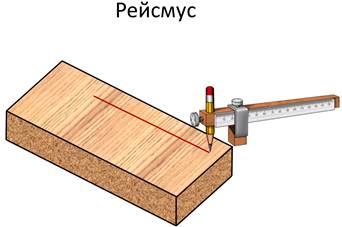
Кстати, прибор, которым пользуются плотник и столяр для построения линии параллельной краю доски называется рейсмус.
Вернёмся к чертежу, на котором мы строили параллельные прямые.
Посмотрите внимательно на рисунок: прямая t параллельна прямой k. Кроме того, прямая d параллельна прямой k. Не сложно убедиться, что прямые t и d тоже параллельны.
То есть, если две прямые на плоскости параллельны третьей прямой, то они параллельны.
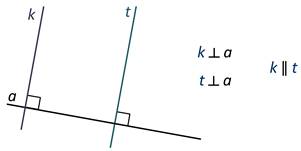
А это значит, что если вдоль другой стороны угольника провести прямую а, то эта прямая будет перпендикулярна прямой k. Кроме того, прямая t будет перпендикулярна прямой а.
А сами прямые k и t параллельны.
То есть, если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.
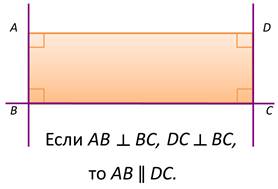
Например, если продлить смежные (то есть соседние) стороны прямоугольника, то полученные прямые будут перпендикулярны.
А значит, противоположные стороны прямоугольника будут параллельны.
Кроме параллельных прямых в математике есть понятие «параллельные отрезки (или лучи)».
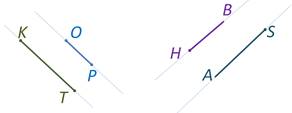
Отрезки (или лучи), лежащие на параллельных прямых называются параллельными.
Например, отрезки KT и OP параллельны, т.к. через них можно провести параллельными прямые. Лучи SA и HB лежат на параллельных прямых, а значит параллельны.
Приведём примеры параллельных прямых в окружающей обстановке.
Посмотрите внимательно, противоположные стороны картины параллельны. Кроме того, параллельные отрезки можно найти и на двери, и на окне, и даже на обоях.
Две непересекающиеся прямые на плоскости называются параллельными.
Если две прямые на плоскости параллельны третьей прямой, то они параллельны.
Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.
Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.