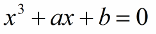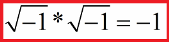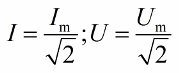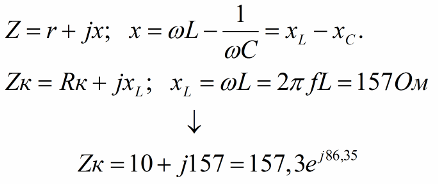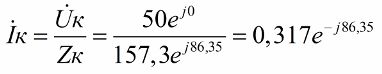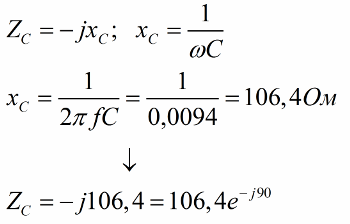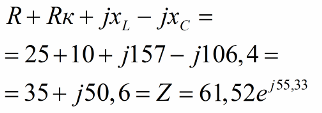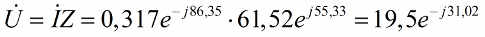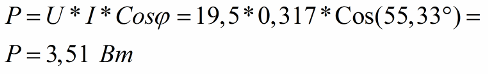что такое омега в электротехнике
Переменный (синусоидальный) ток и основные характеризующие его величины.
Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
В быту для электроснабжения переменяется переменный, синусоидальный ток.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):
Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
Период Т— это время, за которое совершается одно полное колебание.
f = 1/T
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2
Рисунок 2. Радиан.
1рад = 360°/2
? = 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Чему равна омега в физике
| Угловая частота | |
|---|---|
| ω | |
| Размерность | T −1 |
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы | градус/с |
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
Угловая частота связана с частотой ν соотношением [1]
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2 π единиц времени.
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2 π и 1/(2 π ), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
| В Викисловаре есть статья « омега » |
Омега (греч. ὦ μέγα — большое «о») — последняя буква греческого алфавита. А также:
Содержание
Омега в математике и информатике [ править | править код ]
Омега в химии и физике [ править | править код ]
Омега в астрономии [ править | править код ]
Топонимы [ править | править код ]
Подразделения специального назначения [ править | править код ]
Музыкальные группы и произведения [ править | править код ]
Автомашины [ править | править код ]
«Омега» как марка технических устройств [ править | править код ]
«Омега» в художественных произведениях, кинематографии и компьютерных играх [ править | править код ]
•Омега-персонаж из fortnite
Рассмотрите угловую скорость вращения тела в физике: определение, как объект вращается с угловой скоростью, формула решения задач, угловая и линейная скорость.
Чтобы проверить стремительность вращения тела, представим угловую скорость ω как скорость изменения угла:
Чем больше угол поворота за предложенный временной промежуток, тем выше угловая скорость. Единица – радиан в секунду.
Угловая скорость (ω) соответствует линейной (v). Чтобы отыскать точное соотношение между ними, рассмотрим углубление на вращающемся компакт-диске. Оно смещает длину дуги Δs за период Δt и поэтому обладает линейной скоростью v = Δs/Δt.
Из Δθ = (Δs)/r видно, что Δs = r ⋅ Δθ. Подставим в формулу для v, и видим:
v = (r ⋅ Δθ)/(Δt) = r (Δθ/Δt) = rω.
Это можно описать двумя путями: v = rω или ω = v/r.
Из первого видно, что линейная скорость (v) расположена пропорционально дистанции от центра вращения, поэтому ее максимум достигает для точки на ободе. На краю мы можем назвать ее тангенциальной скоростью.
Второе можно рассмотреть на перемещении машины. Обратите внимание на шину. Скорость точки в центре совпадает с показателями v машины. Чем быстрее движение, тем больше оборотов совершает шина, а значит v = rω. Точно также, шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет повышать линейную скорость (v).
Машина, смещающаяся вправо со скоростью v, обладает шиной с угловой скоростью ω. Скорость протектора шины относительно оси приравнивается к v так же, как если бы машину приподняли. Получается, что транспорт перемещается вперед с линейной скоростью v = rω (r – радиус шины). Большая угловая скорость шины приводит к повышению скорости автомобиля
Что означает сопротивление в 1 Ом
Проектирование и эксплуатация электрических приборов и установок во многом зависят от сопротивления материалов. В статье будет подробно рассказано, что из себя представляет величина электрического сопротивления 1 Ом.
Дополнительно будет дано описание обозначения этой единицы и правила замера сопротивления при помощи мультиметра.
Определение
Для того чтобы узнать, что такое за значение 1 Ом, необходимо знать определение электрического сопротивления. Электрическое сопротивление — это физическая величина, определяющая сопротивляемость проводника прохождению электрического тока.
Сопротивление измеряется в Омах. 1 Ом — это сопротивление участка электроцепи, между концами которой протекает электроток в один ампер, а напряжение на его концах при этом равняется одному вольту.
Данная величина обозначается в Омах.
Все существующие материалы имеют физическую способность к проводимости электрического тока. Эти материалы подразделяются на 2 основные группы:
Ом — это в системе СИ единица измерения электрического сопротивления. Эта способность материалов была открыта немецким физиком Георгом Симоном Омом. Параметр проводимости получил свое специальное обозначение — значок Ома или символ Омега «Ω».
Физика в качестве базовой величины сопротивления использует величину 1 Ом. Сила в 1000 Ом имеет сокращенное обозначение 1 кОм. В зависимости от типа проводника, сопротивление может иметь различные значения. В физике максимальное значение сопротивление — 1 Йоттаом (ИОм), которое равняется 10 в 24 степени Ом. Сколько существует различных производных единиц сопротивления, можно увидеть на рисунке ниже.
По причине часто возникающих ошибок при написании, было принято еще одно обозначение Ом для Европейской системы классификации. Во многих технических руководствах вы можете встретить обозначение «ohm».
Важно! В рукописном варианте для обозначения сопротивления используют само слово «Ом», а не греческую букву «Омега». Знак «Ω» используется в электронных технических руководствах и при обозначении параметров радиодеталей.
Параметр проводимости измеряется не только по системе СИ. Существует система СГС, которая определяет проводимость по параметрам длины, веса и времени. Параметр СГС или сантиметр, грамм, секунда. По данной классификации, электрическая проводимость для СГС имеет обозначение СГСR. Величина указывает сопротивление не всего проводника, а только его отдельного участка, с учетом длины и веса. Также учитывается время прохождения заряда в 1 вольт по этому участку.
СГС и обычная электрическая проводимость сильно отличаются. Так одна единица СГСR равняется 9*10 в 11 степени Ом. Данная система не имеет практического применения в радиоэлектронике, по причине того, что многие расчетные величины безмерны. Она используется при расчетах электромагнетизма в системе Гаусса, а также в электродинамике.
Формула расчета
Расчет электрического сопротивления делается по специальной формуле. Она состоит из следующих значений:
Формула выглядит следующим образом: I=U/R.
Зная рабочее напряжение и силу тока, можно легко вычислить рабочее сопротивление. Например, электрическая печь работает от напряжения 240 вольт, при силе тока 2 ампера.
Рабочее сопротивление — определяющий параметр при эксплуатации электрооборудования и его ремонте.
При повышении сопротивления значительно снижается проводимость, а значит и сила тока в цепи. При снижении сопротивления, сильно увеличивается сила тока.
Эти особенности проводников часто используются инженерами. Например, для получения высокой температуры, используется спираль с большим сопротивлением. И наоборот, для того, чтобы загорелась лампа накаливания, используется вольфрамовая спираль с очень низким сопротивлением.
Как известно любое физическое воздействие влечет за собой выделение тепловой энергии. При помощи значения проводимости можно легко рассчитать количество выделяемого тепла или Ватт. Делается это при помощи формулы: Вт=А×Ом.
Замер
Наиболее известная радиодеталь, обладающая стабильным рабочим сопротивлением — резистор. Этот элемент не имеет индуктивности и емкости, поэтому может без потери снижать выходящее сопротивление для стабильной работы других компонентов цепи.
Для того чтобы проверить сопротивление проводника, используется прибор омметр. Мерить также можно электронным мультиметром, оснащенным функцией омметра.
Далее будет описан процесс измерения на примере обычного резистора.
Резисторы получают специальное обозначение на корпусе, равное способности радиодетали проводить электрический ток. При измерении значения не должны сильно отклоняться от эталонных.
Важно! Мерить данный параметр можно только на обесточенной цепи. Перед замером на схеме стоит проверить напряжение на конденсаторах и разрядить их.
Параметр сопротивления можно использовать и для проверки целостности элементов электрической цепи. Для точного определения причины неисправности электрических приборов мастер должен знать рабочее сопротивление устройства или силу тока, при котором оно работает. Если в процессе измерения рабочий параметр увеличился, можно сделать вывод о наличии короткого замыкания в цепи, пригорании контактов или повреждении катушки индуктивности. При значительном снижении параметра увеличится значение силы тока, что станет причиной выгорания конденсаторов, части резисторов, увеличения общей рабочей температуры устройства.
Современные мультиметры имеют функцию «прозвонки» со звуковым оповещением. Этот режим можно легко заменить режимом омметра. При помощи омметра можно мерить целостность жил проводки, определять целостность обмотки электрических двигателей и катушек индуктивности.
Очень часто новички используют параметр электрической проводимости и рабочего напряжения для расчета силы тока для нормального функционирования прибора. Делать подобные расчеты можно только при проектировании, используя формулу: А=В/Ом. Имея уже функциональное устройство расчет может быть неверным, если рабочее сопротивление было завышено/занижено вышедшими из строя элементами цепи.
Заключение
Сопротивление и его единица измерения Ом имеют основополагающее значение. Этот параметр помогает выявить неисправности электронных устройств, проектировать различную аппаратуру. Умея мерить этот параметр и зная, что он означает, мастер сможет выполнить ремонт оборудования любой сложности.
Видео по теме
Почему для расчетов в цепях переменного тока используются комплексные числа
Как известно, для решения некоторых типичных задач электротехники применяют комплексные числа. Но для чего их используют и почему это делают именно так? В этом мы и постараемся разобраться по ходу данной статьи. Дело в том, что комплексный метод, или метод комплексных амплитуд, удобен при расчетах сложных цепей переменного тока. И для начала вспомним немного математических основ:
Как видите, комплексное число z включает в себя мнимую и действительную части, которые между собой различаются и обозначаются в тексте по разному. Само же комплексное число z может быть записано в алгебраической, тригонометрической или показательной форме:
Считается, что представление о мнимых числах начало зарождаться в 1545 году, когда итальянский математик, инженер, философ, медик и астролог Джироламо Кардано в своем трактате «Великое искусство» опубликовал данный метод решения уравнений, где, кстати, признался, что идею ему передал Никколо Тарталья (итальянский математик) за 6 лет до публикации этой работы. В работе Крадано решал уравнения вида:
В процессе решения данных уравнений ученый вынужден был допустить существование некого «нереального» числа, квадрат которого был бы равен минус единице «-1», то есть будто бы существует квадратный корень из отрицательного числа, и если его теперь возвести в квадрат, то получится, соответственно, отрицательное число, стоящее под корнем. Кардано указал правило умножения, согласно которому:
На протяжении трех веков математическое сообщество пребывало в процессе привыкания к новому подходу, предложенному Кардано. Мнимые числа постепенно приживались, однако принимались математиками неохотно. И лишь с публикациями работ Гаусса по алгебре, где он доказывал основную теорему алгебры, комплексные числа наконец-то основательно приняли, на дворе был 19 век.
Мнимые числа стали настоящей палочкой — выручалочкой для математиков, ведь сложнейшие задачи стали решаться гораздо проще с приятием существования мнимых чисел.
Так вскоре дело дошло и до электротехники. Электрические цепи переменного тока порой оказывались очень сложными, и для их расчета приходилось вычислять множество интегралов, что зачастую весьма неудобно.
Наконец, в 1893 году гениальный электротехник Карл Август Штейнмец выступает в Чикаго на Международном электротехническом конгрессе с докладом «Комплексные числа и их применение в электротехнике», чем фактически знаменует начало практического применения инженерами комплексного метода расчетов электрических цепей переменного тока.
Из курса физики нам известно, что переменный ток — это такой ток, который изменяется во времени как по величине, так и по направлению.
В технике встречаются различные формы переменного тока, однако наиболее распространен сегодня ток переменный синусоидальный, именно такой используется всюду, при помощи него электроэнергия передается, в виде переменного тока она генерируется, преобразуется трансформаторами и потребляется нагрузками. Синусоидальный ток периодически изменяется по синусоидальному (гармоническому) закону.
Действующие значения тока и напряжения меньше амплитудных значений в корень из двух раз:
В комплексном методе действующие значения токов и напряжений записывают так:
Обратите внимание, что в электротехнике мнимая единица обозначается буквой «j», поскольку буква «i» уже занята здесь для обозначения тока.
Из закона Ома определяют комплексное значение сопротивления:
Сложение и вычитание комплексных значений осуществляется в алгебраической форме, а умножение и деление — в показательной форме.
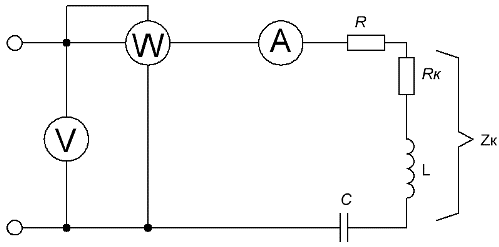
Давайте разберем метод комплексных амплитуд на примере конкретной схемы с определенными значениями основных параметров.
Пример решения задачи с применением комплексных чисел
напряжение на катушке 50 В,
сопротивление резистора 25 Ом,
индуктивность катушки 500 мГн,
электроемкость конденсатора 30 мкф,
сопротивление провода катушки 10 Ом,
частота сети 50 Гц.
Найти: показания амперметра и вольтметра, а также ваттметра.
Для начала запишем комплексное сопротивление последовательно соединенных элементов, которое состоит из действительной и мнимой частей, затем найдем комплексное сопротивление активно-индуктивного элемента.
Вспоминаем! Для получения показательной формы находят модуль z, равный корню квадратному из суммы квадратов действительной и мнимой частей, а также фи, равное арктангенсу частного от деления мнимой части на действительную.
Далее найдем ток и соответственно показания амперметра:
Итак, амперметр показывает ток 0,317 А — это ток через всю последовательную цепь.
Теперь найдем емкостное сопротивление конденсатора, затем определим его комплексное сопротивление:
Далее вычислим полное комплексное сопротивление данной цепи:
Теперь найдем действующее напряжение, приложенное к цепи:
Вольтметр покажет действующее напряжение 19,5 вольт.
Наконец, найдем мощность, которую покажет ваттметр с учетом разности фаз между током и напряжением
Ваттметр покажет 3,51 Ватт.
Теперь вы понимаете, какое важное место комплексные числа занимают в электротехнике. Они применяются для удобного расчета электрических цепей. На этой же основе работают и многие электронные измерительные приборы.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети: