что такое напряжение на концах проводника
Электрический ток и закон Ома
теория по физике 🧲 постоянный ток
Электрический ток — направленное движение заряженных частиц под действием внешнего электрического поля.
Условия существования электрического тока:
Носители электрического тока в различных средах
| Среда | Носители электрического тока |
| Металлы | Свободные электроны |
| Электролиты (вещества, проводящие ток вследствие диссоциации на ионы) | Положительные и отрицательные ионы |
| Газы | Ионы и электроны |
| Полупроводники | Электроны и дырки (атом, лишенный одного электрона) |
| Вакуум | Электроны |
Электрическая цепь и ее схематическое изображение
Электрическая цепь — это совокупность устройств, соединенных определенным образом, которые обеспечивают путь для протекания электрического тока.
Основные элементы электрической цепи:
Электрическая цепь также может содержать:
Электрическая схема — графическое изображение электрической цепи, в котором реальные элементы представлены в виде условных обозначений.
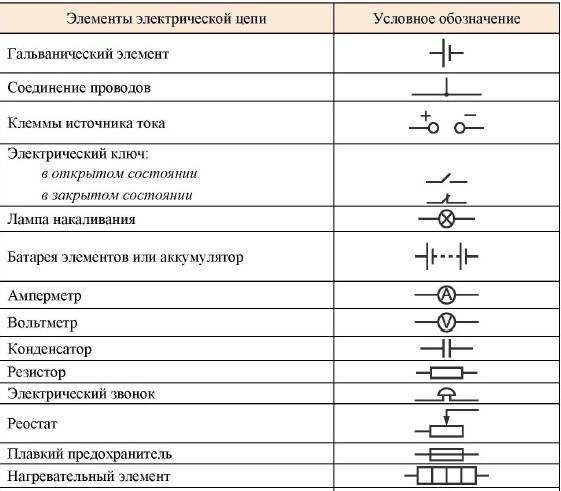
Условные обозначения некоторых элементов электрической цепи
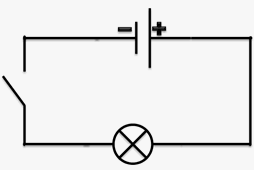
Простейшая электрическая цепь содержит в себе источник и потребитель тока, проводники, ключ. Схематически ее можно отобразить так:
Направление электрического тока в металлах
По металлическим проводам перемещаются отрицательно заряженные электроны, т.е. ток идет от «–» к «+» источника. Направление движения электронов называют действительным. Но исторически в науке принято условное направление тока от «+» источника к «–».
Действия электрического тока (преобразования энергии)
Электрический ток способен вызывать различные действия:
Основные параметры постоянного тока
Постоянный ток — электрический ток, который с течением времени не изменяется по величине и направлению.
Основными параметрами электрического тока являются:
Сила тока
Сила тока показывает, какой заряд q проходит через поперечное сечение проводника за 1 секунду:
Заряд, проходящий по проводнику за время t при силе тока, равной I:
Пример №1. Источник тока присоединили к двум пластинам, опущенным в раствор поваренной соли. Сила тока в цепи 0,2 А. Какой заряд проходит между пластинами в ванне за 2 минуты?
2 минуты = 120 секунд
Заряд, проходящий за время ∆t при равномерном изменении силы тока от I1 до I2:
Сила тока и скорость движения электронов:
n — (м –3 ) — концентрация, S (м 2 ) — площадь сечения проводника, v — скорость электронов.
Внимание!
Электроны движутся по проводам со скоростью, равной долям мм/с. Но электрическое поле распространяется со скоростью света: c = 3∙10 8 м/с.
Сопротивление
Сопротивление металлов характеризует тормозящее действие положительных ионов кристаллической решетки на движение свободных электронов:
Пример №2. Медная проволока имеет электрическое сопротивление 6 Ом. Какое электрическое сопротивление имеет медная проволока, у которой в 2 раза больше длина и в 3 раза больше площадь поперечного сечения?
Сопротивление первого и второго проводника соответственно:
Поделим электрическое сопротивление второго проводника на сопротивление первого:
Отсюда сопротивление второго проводника равно:
Напряжение
Напряжение характеризует работу электрического поля по перемещению положительного заряда:
Пример №3. Перемещая заряд в первом проводнике, электрическое поле совершает работу 20 Дж. Во втором проводнике при перемещении такого же заряда электрическое поле совершает работу 40 Дж. Определить отношение U1/U2 напряжений на концах первого и второго проводников.
Закон Ома для участка цепи
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению:
Иллюстрация закона Ома.
Сила тока направлена в сторону движения заряженных частиц (электронов). Силе тока противостоит сопротивление: чем оно больше, тем меньше сила тока (тем меньше проходит электронов через проводник в единицу времени). Но росту силы тока способствует напряжение, которое словно толкает заряженные частицы, заставляя их упорядоченно перемещаться.
Закон Ома для участка цепи с учетом формулы для расчета сопротивления:
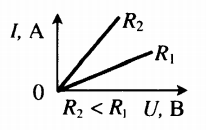
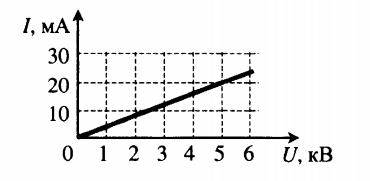
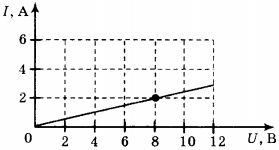
Для сравнения и расчета сопротивления часто используют вольтамперную характеристику. Так называют графическое представление зависимости силы тока от напряжения. Пример вольтамперной характеристики:
Чем круче график, тем меньше сопротивление проводника. При расчете сопротивления важно учитывать единицы измерения величин, указанных на осях.
Пример №4. На рисунке изображен график зависимости силы тока от напряжения на одной секции телевизора. Каково сопротивление этой секции:
Точке графика, соответствующей 5 кВ, соответствует сила тока, равна 20 мА.
Сначала переведем единицы измерения величин в СИ:
При определении сопротивления резистора ученик измерил напряжение на нём: U = (4,6 ± 0,2) В. Сила тока через резистор измерялась настолько точно, что погрешностью можно пренебречь: I = 0,500 А. По результатам этих измерений можно сделать вывод, что сопротивление резистора, скорее всего,
Постоянный электрический ток. Сила тока. Напряжение. Электрическое сопротивление. Закон Ома для участка электрической цепи
1. Электрическим током называют упорядоченное движение заряженных частиц.
Для того чтобы в проводнике существовал электрический ток, необходимы два условия: наличие свободных заряженных частиц и электрического поля, которое создаёт их направленное движение.
При существовании тока в разных средах: в металлах, жидкостях, газах — электрический заряд переносится разными частицами. В металлах этими частицами являются электроны, в жидкостях заряд переносится ионами, в газах — электронами, положительными и отрицательными ионами.
Дистиллированная вода не проводит электрический ток, поскольку она не содержит свободных зарядов. Если в воду добавить поваренную соль или медный купорос, то в ней появятся свободные заряды, и она станет проводником электрического тока. В растворе поваренной соли в воде происходит электролитическая диссоциация — процесс разложения молекулы поваренной соли на положительный ион натрия и отрицательный ион хлора. Если в сосуд с раствором поваренной соли поместить две металлические пластины, соединённые с источником тока (рис. 79), то положительный ион натрия в электрическом поле будет двигаться к пластине, соединенной с отрицательным полюсом источника тока, называемым катодом, а отрицательный ион хлора — с положительным полюсом источника тока, называемым анодом.
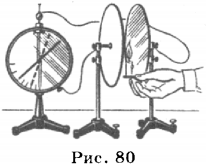
Газы в обычных условиях тоже не проводят электрический ток, так как в них нет свободных зарядов. Однако если в воздушный промежуток между двумя металлическими пластинами, соединёнными с источником тока, внести зажжённую спичку или спиртовку, то газ станет проводником и гальванометр зафиксирует протекание тока но цепи. При внесении пламени в воздушный промежуток между пластинами происходит ионизация газа (рис. 80). При этом от атома «отрываются» электроны и образуется положительный ион. Во время движения электрон может присоединиться к нейтральному атому и образовать отрицательный ион. Положительные ионы движутся к отрицательному электроду, а отрицательные ионы и электроны — к положительному электроду.
2. Направленное движение зарядов обеспечивается электрическим полем. Электрическое поле в проводниках создаётся и поддерживается источником тока. В источнике тока совершается работа по разделению положительно и отрицательно заряженных частиц. Эти частицы накапливаются на полюсах источника тока. Один полюс источника заряжается положительно, другой — отрицательно. Между полюсами источника образуется электрическое поле, под действием которого заряженные частицы начинают двигаться упорядоченно.
В источнике тока совершается работа при разделении заряженных частиц. При этом различные виды энергии превращаются в электрическую энергию. В электрофорной машине в электрическую энергию превращается механическая энергия, в гальваническом элементе — химическая.
3. Электрический ток, проходя по цепи, производит различные действия. Тепловое действие электрического тока заключается в том, что при его прохождении по проводнику в нём выделяется некоторое количество теплоты. Пример применения теплового действия тока — электронагревательные элементы чайников, электроплит, утюгов и пр. В ряде случаев температура проводника нагревается настолько сильно, что можно наблюдать его свечение. Это происходит в электрических лампочках накаливания.
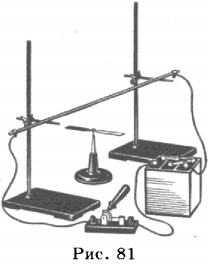
Магнитное действие электрического тока проявляется в том, что вокруг проводника с током возникает магнитное поле, которое, действуя на магнитную стрелку, расположенную рядом с проводником, заставляет её поворачиваться (рис. 81).
Благодаря магнитному действию тока можно превратить железный гвоздь в электромагнит, намотав на него провод, соединённый с источником тока. При пропускании по проводу электрического тока гвоздь будет притягивать железные предметы.
Химическое действие электрического тока проявляется в том, что при его прохождении в жидкости на электроде выделяется вещество. Если в стакан с раствором медного купороса поместить угольные электроды и присоединить их к источнику тока, то, вынув через некоторое время эти электроды из раствора, можно обнаружить на электроде, присоединённом к отрицательному полюсу источника (на катоде), слой чистой меди.
Это происходит потому, что между электродами существует электрическое поле, в котором ионы (положительно заряженные ионы меди и отрицательно заряженные ионы кислотного остатка) движутся к соответствующим электродам. Достигнув отрицательного электрода, ионы меди получают недостающие электроны, при этом восстанавливается чистая медь.
4. Характеристикой тока в цепи служит величина, называемая силой тока \( (I) \) . Силой тока называют физическую величину, равную отношению заряда \( q \) , проходящего через поперечное сечение проводника за промежуток времени \( t \) , к этому промежутку времени: \( I=q/t \) .
Определение единицы силы тока основано на магнитном действии тока, в частности на взаимодействии параллельных проводников, по которым идёт электрический ток. Такие проводники притягиваются, если ток по ним идёт в одном направлении, и отталкиваются, если направление тока в них противоположное.
Эта единица называется ампером (1 А).
Зная формулу силы тока, можно получить единицу электрического заряда: 1 Кл = 1 А · 1 с.
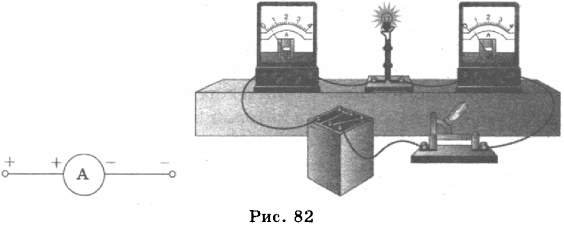
5. Прибор, с помощью которого измеряют силу тока в цепи, называется амперметром. Его работа основана на магнитном действии тока. Основные части амперметра магнит и катушка. При прохождении по катушке электрического тока она в результате взаимодействия с магнитом, поворачивается и поворачивает соединённую с ней стрелку. Чем больше сила тока, проходящего через катушку, тем сильнее она взаимодействует с магнитом, тем больше угол поворота стрелки. Амперметр включается в цепь последовательно с тем прибором, силу тока в котором нужно измерить (рис. 82), и потому он имеет малое внутреннее сопротивление, которое практически не влияет на сопротивление цепи и на силу тока в цепи.
У клемм амперметра стоят знаки «+» и «-», при включении амперметра в цепь клемма со знаком «+» присоединяется к положительному полюсу источника тока, а клемма со знаком «-» к отрицательному полюсу источника тока.
6. Источник тока создаёт электрическое поле, которое приводит в движение электрические заряды. Характеристикой источника тока служит величина, называемая напряжением. Чем оно больше, тем сильнее созданное им поле. Напряжение характеризует работу, которую совершает электрическое поле по перемещению электрического заряда, равного 1 Кл.
Напряжением \( U \) называют физическую величину, равную отношению работы \( (A) \) электрического поля по перемещению электрического заряда к заряду \( (q) \) : \( U=A/q \) .
Возможно другое определение понятия напряжения. Если числитель и знаменатель в формуле напряжения умножить на время движения заряда \( (t) \) , то получим: \( U=At/qt \) . В числителе этой дроби стоит мощность тока \( (P) \) , а в знаменателе — сила тока \( (I) \) : \( U=P/I \) , т.е. напряжение — физическая величина, равная отношению мощности электрического тока к силе тока в цепи.
Единица напряжения: \( [U]=[A]/[q] \) ; \( [U] \) = 1 Дж/1 Кл = 1 В (один вольт).
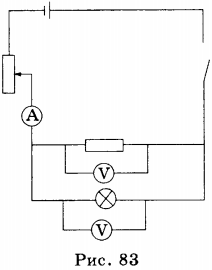
Напряжение измеряют вольтметром. Он имеет такое же устройство, что и амперметр и такой же принцип действия, но он подключается параллельно тому участку цепи, напряжение на котором хотят измерить (рис. 83). Внутреннее сопротивление вольтметра достаточно большое, соответственно проходящий через него ток мал по сравнению с током в цепи.
У клемм вольтметра стоят знаки «+» и «-», при включении вольтметра в цепь клемма со знаком «+» присоединяется к положительному полюсу источника тока, а клемма со знаком «-» к отрицательному полюсу источника тока.
7. Собрав электрическую цепь, состоящую из источника тока, резистора, амперметра, вольтметра, ключа (рис. 83), можно показать, что сила тока \( (I) \) , протекающего через резистор, прямо пропорциональна напряжению \( (U) \) на его концах: \( I\sim U \) . Отношение напряжения к силе тока \( U/I \) — есть величина постоянная. Если заменить резистор, включённый в цепь, другим резистором и повторить опыт, получим тот же результат: сила тока в резисторе прямо пропорциональна напряжению на его концах, а отношение напряжения к силе тока есть величина постоянная. Только в этом случае значение отношения напряжения к силе тока будет отличаться от отношения этих величин в первом опыте. Причиной этого является то, что в цепь включались разные резисторы. Следовательно, существует физическая величина, характеризующая свойства проводника (резистора), по которому течёт электрический ток. Эту величину называют электрическим сопротивлением проводника, или просто сопротивлением. Обозначается сопротивление буквой \( R \) .
Сопротивлением проводника \( (R) \) называют физическую величину, равную отношению напряжения \( (U) \) на концах проводника к силе тока \( (I) \) в нём. \( R=U/I \) .
За единицу сопротивления принимают Ом (1 Ом).
Один Ом — сопротивление такого проводника, в котором сила тока равна 1 А при напряжении на его концах 1 В: 1 Ом = 1 В/1 А.
Причина того, что проводник обладает сопротивлением, заключается в том, что направленному движению электрических зарядов в нём препятствуют ионы кристаллической решетки, совершающие беспорядочное движение. Соответственно, скорость направленного движения зарядов уменьшается.
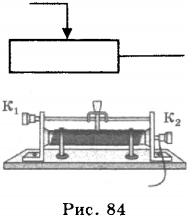
Изменяя длину проводника, а следовательно его сопротивление, можно регулировать силу тока в цепи. Прибор, с помощью которого это можно сделать, называется реостатом (рис. 84).
9. Как показано выше, сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: \( I=\frac
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
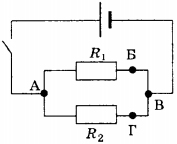
1. На рисунке приведена схема электрической цепи, состоящей из источника тока, ключа и двух параллельно соединённых резисторов. Для измерения напряжения на резисторе \( R_2 \) вольтметр можно включить между точками
1) только Б и В
2) только А и В
3) Б и Г или Б и В
4) А и Г или А и В
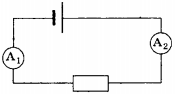
2. На рисунке представлена электрическая цепь, состоящая из источника тока, резистора и двух амперметров. Сила тока, показываемая амперметром А1, равна 0,5 А. Амперметр А2 покажет силу тока
1) меньше 0,5 А
2) больше 0,5 А
3) 0,5 А
4) 0 А
3. Ученик исследовал зависимость силы тока в электроплитке от приложенного напряжения и получил следующие данные.
Проанализировав полученные значения, он высказал предположения:
А. Закон Ома справедлив для первых трёх измерений.
Б. Закон Ома справедлив для последних трёх измерений.
Какая(-ие) из высказанных учеником гипотез верна(-ы)?
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
4. На рисунке изображён график зависимости силы тока в проводнике от напряжения на его концах. Чему равно сопротивление проводника?
1) 0,25 Ом
2) 2 Ом
3) 4 Ом
4) 8 Ом
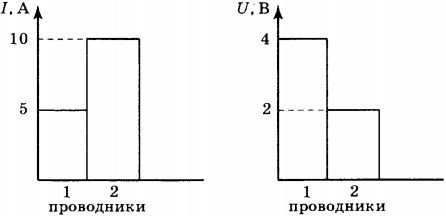
5. На диаграммах изображены значения силы тока и напряжения на концах двух проводников. Сравните сопротивления этих проводников.
1) \( R_1=R_2 \)
2) \( R_1=2R_2 \)
3) \( R_1=4R_2 \)
4) \( 4R_1=R_2 \)
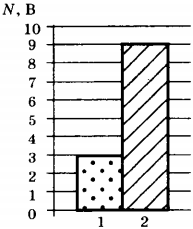
6. На рисунке приведена столбчатая диаграмма. На ней представлены значения мощности тока для двух проводников (1) и (2) одинакового сопротивления. Сравните значения напряжения \( U_1 \) и \( U_2 \) на концах этих проводников.
1) \( U_2=\sqrt<3>U_1 \)
2) \( U_1=3U_2 \)
3) \( U_2=9U_1 \)
4) \( U_2=3U_1 \)
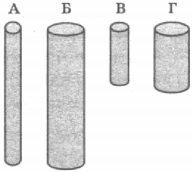
7. Необходимо экспериментально обнаружить зависимость электрического сопротивления круглого угольного стержня от его длины. Какую из указанных пар стержней можно использовать для этой цели?
1) А и Г
2) Б и В
3) Б и Г
4) В и Г
1) Сопротивление первого проводника в 64 раза больше, чем второго.
2) Сопротивление первого проводника в 8 раз больше, чем второго.
3) Сопротивление второго проводника в 64 раза больше, чем первого.
4) Сопротивление второго проводника в 8 раз больше, чем первого.
9. В течение 600 с через потребитель электрического тока проходит заряд 12 Кл. Чему равна сила тока в потребителе?
1) 0,02 А
2) 0,2 А
3) 5 А
4) 50 А
10. В таблице приведены результаты экспериментальных измерений площади поперечного сечения \( S \) , длины \( L \) и электрического сопротивления \( R \) для трёх проводников, изготовленных из железа или никелина.
На основании проведённых измерений можно утверждать, что электрическое сопротивление проводника
1) зависит от материала проводника
2) не зависит от материала проводника
3) увеличивается при увеличении его длины
4) уменьшается при увеличении его площади поперечного сечения
11. Для изготовления резисторов использовался рулон нихромовой проволоки. Поочередно в цепь (см. рисунок) включали отрезки проволоки длиной 4 м, 8 м и 12 м. Для каждого случая измерялись напряжение и сила тока (см. таблицу).
Какой вывод можно сделать на основании проведённых исследований?
1) сопротивление проводника обратно пропорционально площади его поперечного сечения
2) сопротивление проводника прямо пропорционально его длине
3) сопротивление проводника зависит от силы тока в проводнике
4) сопротивление проводника зависит от напряжения на концах проводника
5) сила тока в проводнике обратно пропорциональна его сопротивлению
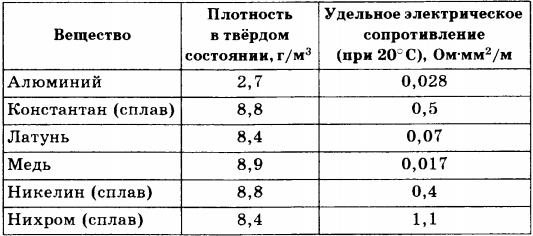
12. В справочнике физических свойств различных материалов представлена следующая таблица.
Используя данные таблицы, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) При равных размерах проводник из алюминия будет иметь меньшую массу и большее электрическое сопротивление по сравнению с проводником из меди.
2) Проводники из нихрома и латуни при одинаковых размерах будут иметь одинаковые электрические сопротивления.
3) Проводники из константана и никелина при одинаковых размерах будут иметь разные массы.
4) При замене никелиновой спирали электроплитки на нихромовую такого же размера электрическое сопротивление спирали уменьшится.
5) При равной площади поперечного сечения проводник из константана длиной 4 м будет иметь такое же электрическое сопротивление, что и проводник из никелина длиной 5 м.
Часть 2
13. Меняя электрическое напряжение на участке цепи, состоящем из никелинового проводника длиной 5 м, ученик полученные данные измерений силы тока и напряжения записал в таблицу. Чему равна площадь поперечного сечения проводника?
О природе электрического тока и основах электротехники
В данной короткой статье попытаюсь на пальцах объяснить основы электротехники. Для тех, кто не понимает откуда в розетке электричество, но спрашивать вроде как уже неприлично.
1. Что такое электрический ток.
«Главный инженер повернул рубильник, и электрический ток все быстрее и быстрее побежал по проводам» (с)
Будем рассматривать ток в металлических проводниках, который создаётся электронами. Можно провести аналогию между электронами в проводнике и жидкости в водопроводной трубе. (На начальном этапе электричество так и считали особой жидкостью.) Как через стенки трубы вода не выливается, так и электроны не могут покинуть проводник, потому что положительно заряженные ядра атомов притянут их обратно. Электроны могут перемещаться только в внутри проводника.
1.2 Создание электрического тока.
Но просто так ток в проводнике не возникнет. Это все равно, что залить воду в кусок трубы и заварить с обоих концов. Вода никуда не потечет. В куске проводника электроны тоже не могут двигаться в одном направлении. Если электроны почему-то сдвинутся вправо, то слева возникнет нескомпенсированный положительный заряд, который потянет их обратно. Поэтому электроны могут только прыгать от одного атома к другому и обратно. Но если трубу свернуть в кольцо, то вода уже может течь вдоль трубы, если каким-то образом заставить ее двигаться. Точно также и концы проводника можно соединить друг с другом, и тогда электроны смогут перемещаться вдоль проводника, если их заставить. Если концы проводника соединены друг с другом, то получается замкнутая цепь. Постоянный ток может идти только в замкнутой цепи. Если цепь разомкнута, то ток не идет. Чтобы заставить воду течь по трубе используется насос. В электрической цепи роль насоса выполнят батарейка. Батарейка гонит электроны по проводнику и тем самым создает электрический ток. По научному батарейка называется генератором. Так в электротехнике называют насос для создания электрического тока.



Рассмотрим теперь цепь с генератором тока.

2. Закон Ома.
Сначала c точки зрения генератора напряжения
Если к сопротивлению R приложить напряжение U, то через сопротивление пойдет ток
I =U/R Теперь с точки зрения генератора тока
Если через сопротивление R пропускать ток I, то на сопротивлении возникнет падение напряжения U=I*R

Хотя пару важных практических случаев все таки рассмотрим.
3. Делитель напряжения
Схема имеет вид.

Делитель напряжения представляет собой два резистора, соединенных последовательно друг с другом.
Так вот. Что же делает эта схема? Два последовательных резистора имеют некоторое эквивалентное сопротивление, назовем его R12. По цепи проходит ток I, от плюса генератора к минусу через резистор R1 и через резистор R2. При этом на резисторе R1 падает напряжение U1=I*R1, а на резисторе R2 падает напряжение U2=I*R2. Согласно закону Ома. Напряжение U=U1+U2, как видно из схемы. Таким образом U=I*R1+I*R2=I*(R1+R2).
То есть эквивалентное сопротивление последовательно соединенных резисторов равно сумме их сопротивлений.
Выражение для тока I=U/(R1+R2)
Найдем теперь, чему равно напряжение U2. U2=I*R2= U* R2/(R1+R2).
Пример картинки из интернета. Если резисторы равны, то входное напряжение Uвx делится пополам.

Идеальный генератор напряжения имеет нулевое выходное сопротивление, то есть при нулевом сопротивлении внешней цепи величина тока будет равна бесконечности ∝. Реальный генератор напряжения обеспечить бесконечный ток не может. Поэтому при замыкании внешней цепи ток в ней будет ограничен внутренним сопротивлением генератора, на рис. обозначен буквой r.
Кстати, правильный способ проверки пальчиковых батареек, заключается в измерении тока, которые они могут отдать. То есть на тестере выставляется предел 10А, режим измерения тока, и щупы прикладываются к контактам батареи. Ток в районе 1А или больше говорит о том, что батарейка свежая. Если ток меньше 0.5А, то можно выкидывать. Или попробовать в настенных часах, может сколько-то проработает.
Если выходное сопротивление источника (внутреннее сопротивление r на рисунке) соизмеримо со входным сопротивлением приемника (R3 на рисунке), то эти резисторы будут действовать, как делитель напряжения. На приемник при этом будет поступать не полное напряжение источника U, а U1=U*R3/(r+R3). Если эта схема предназначена для измерения напряжения U, то она будет врать!
В следующих статьях планируется рассмотреть цепи с конденсаторами и индуктивностями.
Затем диоды, транзисторы и операционные усилители.