Что такое компьютерная математическая модель
Знаковые модели. Компьютерные математические модели
Урок 4. Информатика 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Знаковые модели. Компьютерные математические модели»
· Определение компьютерной математической модели.
· Использование компьютерной математических моделей.
· Применение при решении задач.
Самые разные математические модели широко использовались и используются при изучении многих научных областей и дисциплин. Так, на пример, учёные астрономы используют математические модели, чтобы предсказать движение небесных тел. Как мы уже знаем, при составлении любых информационных моделей учитываются существенные свойства объекта или явления. Но что делать, если этих свойств очень много или они очень сложны для расчёта? Ведь человеку понадобится немало времени для реализации такой математической модели.
Реализация – это расчёт состояния объекта или системы, по формулам из математической модели, которые связывают значения его исходных и результирующих параметров.
Это одна из важнейших областей применения компьютеров. Ведь компьютер способен выполнять миллионы математических операций в секунду.
Математические модели, реализованные на компьютере с помощью тех или иных программных средств, называются компьютерными математическими моделями.
Для реализации математических моделей на компьютере могут использоваться:
· различные языки программирования,
· различные математические пакеты.
При использовании некоторых средств визуализации можно наглядно представить результаты и процесс работы той или иной системы.
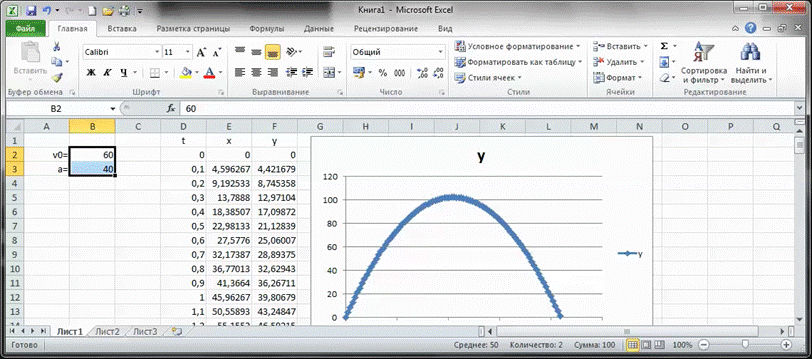
Реализация математической модели в Microsoft Excel
После того, как математическая модель была задана достаточно нескольких нажатий клавиш, чтобы изменить исходные данные системы. И мы тут же получили результирующие данные для системы с другими параметрами.
Особую роль среди компьютерных математических моделей занимают модели систем, параметры которых могут принимать случайные значения в определённых пределах. Часто для того, чтобы оптимизировать работу такой системы, моделируют её работу при различных параметрах и находят их оптимальные значения. Такая математическая модель называется имитационной.
Имитационные модели применяются во многих сферах жизни человека. Например, моделирование системы обслуживания покупателей в магазине, чтобы выяснить, какое количество продавцов необходимо для нормальной его работы. Ведь мы не можем точно предсказать количество покупателей, пришедших в магазин за единицу времени или точное время обслуживания продавцом каждого из них.
Подобные модели могут применяться во многих областях науки. Рассмотрим пример из теории вероятности. Хорошо известно, что вероятность выпадения герба или цифры при подбрасывании монеты равна 50%, но как это проверить? Можно много раз подбросить монету, записывая результат. При этом очевидно, что чем большее число подбрасываний мы совершим, тем результат будет точнее. Некоторые математики проделывали этот опыт. Результаты некоторые результаты представлены в таблице.